粒子濾波重采樣及在盲均衡中的應(yīng)用

付何偉， 金明錄， 崔承毅

（大連理工大學(xué) 電信學(xué)院，遼寧 大連 116024）

0 引言

早在20世紀(jì)50年代Hammersley等人就提出序貫重要性采樣（SIS）的方法，但其容易導(dǎo)致粒子退化現(xiàn)象，影響了它在實(shí)際中的應(yīng)用。直到1993年，Gordon等人提出了采樣重要性重采樣算法 SIR[1]這一概念，解決了粒子濾波算法粒子退化的問題，粒子濾波才又被廣泛關(guān)注，并在各個(gè)領(lǐng)域得到了應(yīng)用。

由于粒子濾波在處理非線性非高斯問題上的優(yōu)越性，一些學(xué)者對(duì)粒子濾波的盲均衡算法進(jìn)行了研究，表明在信噪比較低的情況下，仍具有較好的均衡效果。近年來，各種情況下的粒子濾波盲均衡算法被廣泛研究，如文獻(xiàn)[2-3]的時(shí)不變信道，文獻(xiàn)[4-5]的時(shí)變信道，文獻(xiàn)[6]的加性高斯和非高斯信道等。

1 粒子濾波理論

粒子濾波算法是一種應(yīng)用粒子集表示概率的蒙特卡羅方法，它的主要思想是用一個(gè)隨機(jī)采樣獲得具有權(quán)重的樣本集合表示并估計(jì)后驗(yàn)概率密度。基本算法包括兩個(gè)部分：①SIS；②SIR。接下來，分別介紹這兩部分。

1.1 SIS

SIS的核心思想是利用一系列隨機(jī)樣本的加權(quán)和表示所需的后驗(yàn)概率密度，從而得到狀態(tài)的估計(jì)值。

假定狀態(tài)方程和觀測(cè)方程可表示為：

其中kx為狀態(tài)矢量，ku為狀態(tài)噪聲，ky為觀測(cè)值，kv為獨(dú)立于系統(tǒng)噪聲的觀測(cè)噪聲。

選擇一個(gè)重要性函數(shù) ()qs，假設(shè) ()qs可以分解為：

根據(jù)重要概率密度 q (xk|x0:k-1, y0:k)中抽取粒子，則每個(gè)粒子的權(quán)重可表示為：

此后，對(duì)權(quán)值進(jìn)行歸一化，得：

1.2 SIR

SIS算法容易出現(xiàn)粒子退化現(xiàn)象，為此引入了重采樣的概念。重采樣可以消除低重要性權(quán)值的樣本，同時(shí)增加高重要性權(quán)值的樣本。

1.2.1 多項(xiàng)式重采樣

1993年由Gordon等人提出的多項(xiàng)式重采樣[1]是各種重采樣的基礎(chǔ)，基本解決了粒子濾波的退化問題。若粒子數(shù)為n,算法步驟如下：①對(duì)于粒子1in≤≤，在（0,1]區(qū)間按均勻分布采樣得到 n個(gè)采樣值iu；②產(chǎn)生粒子權(quán)重累積函數(shù)sumweight,滿足 sumweight(i)=；③當(dāng)sumweight(k)＜u(i)時(shí)，將第k個(gè)粒子經(jīng)重采樣后被復(fù)制在第i個(gè)位置上；④每個(gè)粒子的權(quán)重設(shè)為1/n。

1.2.2 分層重采樣

1999年由Carpenter等人提出的分層重采樣，對(duì)多項(xiàng)式算法進(jìn)行改進(jìn)，將無序的隨機(jī)數(shù)變?yōu)橛行颉?0,1]分成n個(gè)連續(xù)互不重合的空間，即：(0,1]= (0,1/ n]U…U((n -1)/ n,1]。再對(duì)每個(gè)子空間獨(dú)立同分布采樣得到iu，即：iu=U((i-1)/n, i / n)其中U（a,b）表示區(qū)間[a,b]上的均勻分布。

1.2.3 系統(tǒng)重采樣

系統(tǒng)重采樣與分層重采樣類似，但每個(gè)iu的產(chǎn)生方式不同，若1u～U（0，1/n），則：

1.2.4 降序二分重采樣

多項(xiàng)式重采樣算法采用的隨機(jī)數(shù)集合是均勻分布的，呈現(xiàn)一種無規(guī)律性，當(dāng)這個(gè)集合中的隨機(jī)數(shù)有序排列時(shí)，多數(shù)情況下得到的濾波結(jié)果都優(yōu)于無序時(shí)。而分層重采樣算法將隨機(jī)數(shù)區(qū)間分成n個(gè)連續(xù)但不重合的區(qū)間，對(duì)每個(gè)區(qū)間采樣一個(gè)隨機(jī)數(shù)，這樣得到的分布集合自動(dòng)變?yōu)橛行颍虼藘?yōu)于傳統(tǒng)的多項(xiàng)式重采樣算法。但是，從濾波結(jié)果來看，有時(shí)分層重采樣算法反而不及多項(xiàng)式重采樣算法。鑒于這種情況，現(xiàn)提出一種改進(jìn)算法—降序二分重采樣算法，它的主要思想是在分層重采樣算法的基礎(chǔ)上，尋找權(quán)重最大點(diǎn)的過程用折半二分法。仿真結(jié)果表明，這種算法的平均性能要優(yōu)于多項(xiàng)式重采樣算法和分層重采樣算法。

算法步驟如下：①同分層重采樣的第一步；②對(duì)每個(gè)子空間獨(dú)立同分布采樣得到iu，即：iu=U(1- i / n,1-(i-1)/n)；③同多項(xiàng)式重采樣的第二步；④粒子更新過程如下偽代碼所示；⑤最后，每個(gè)粒子的權(quán)重設(shè)為1/n。

for i=1: N

lower=1; upper=N;

while((upper-lower≠1))&(sumweight(k) ≠ u(i))

mean=( upper+lower)/2; redistr=

if(sumweight(redistr)≥u(i))

upper=redistr;

else

lower=redistr;

end

end

redistr=upper;

ind(i) = redistr; (表示第 redistr個(gè)粒子經(jīng)重采樣后被復(fù)制在第i個(gè)位置)

end

2 基于粒子濾波的盲均衡

2.1 系統(tǒng)模型

假設(shè)通信系統(tǒng)傳輸 ut∈ {± 1 }，t=0,1,2,…的二進(jìn)制符號(hào)，通過頻率選擇性衰落信道。當(dāng)相干時(shí)間大于幀長度時(shí)，可以在一個(gè)幀長度內(nèi)把信道沖擊響應(yīng)看成是不變的。通信系統(tǒng)中的信號(hào)模型可采用：

由于粒子濾波的方法需要采用狀態(tài)空間模型，因此將上述模型改寫如下：

2.2 粒子濾波盲均衡

利用粒子濾波器進(jìn)行盲均衡的目的是用具有權(quán)重的隨機(jī)采樣點(diǎn)表示所需要的后驗(yàn)概率密度,并根據(jù)這些采樣點(diǎn)和權(quán)重對(duì)信道和發(fā)送的符號(hào)進(jìn)行估值,從而完成對(duì)信道的辨識(shí)和均衡[7]。采用粒子濾波進(jìn)行盲均衡的流程圖如圖1。

圖1 粒子濾波盲均衡流程

2.2.1 信道的更新

盲均衡是在輸入和信道都未知的情況下，因此假設(shè)輸入ut∈{±1 }為獨(dú)立均勻分布的隨機(jī)變量，信道先驗(yàn)分布服從均值為h-1，方差為 C-1的高斯分布。

經(jīng)過推導(dǎo)可以證明信道的后驗(yàn)分布的均值和方差有如下表達(dá)形式[8]：

由式(10)和式(11)可以更新信道的均值和方差。由于信道的后驗(yàn)分布是服從高斯分布的，均值是其最優(yōu)貝葉斯估計(jì)，所以可以用均值作為信道真實(shí)值的近似，即ht= ht，這樣在對(duì)信道進(jìn)行辨識(shí)過程中就無需對(duì)信道的后驗(yàn)分布進(jìn)行采樣，可以降低算法的計(jì)算量。

2.2.2 權(quán)值的更新

如果從重要性函數(shù) q (x0:t|h,y0:t)中采樣得到粒子（m=1,2,…,M,M 是每一時(shí)刻的粒子個(gè)數(shù)），若選用的重要性函數(shù)可以分解為如下形式：

此時(shí)可得如下結(jié)論[8]：

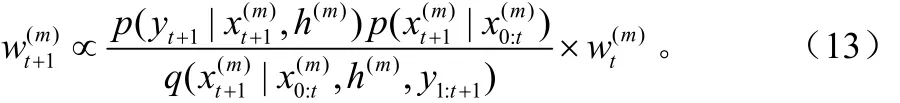
在選擇重要性函數(shù)時(shí)，應(yīng)使其盡可能接近似然函數(shù)，但由于這樣選擇的重要性函數(shù)采樣比較困難，因此采用先驗(yàn)概率密度作為重要性函數(shù)，即用 p (xt+1|xt)代替重要性函數(shù)，這樣由式（13）可得權(quán)重的更新方程為：

3 仿真結(jié)果與分析

仿真實(shí)驗(yàn)中，信源采用BPSK調(diào)制，采用階數(shù)L=3的時(shí)不變信道h=[0.407,0.815,0.407]。

圖2為各種重采樣算法下信道估計(jì)的比較，橫坐標(biāo)為符號(hào)個(gè)數(shù)，縱坐標(biāo)為信道的平均誤差。仿真條件：信噪比為20 dB，發(fā)送的比特?cái)?shù)為1 000，估計(jì)的粒子數(shù)為100，結(jié)果為仿真100次的平均值。四條曲線分別是降序二分法、多項(xiàng)式重采樣、分層重采樣和系統(tǒng)重采樣算法。仿真結(jié)果表明，降序二分法能更快地收斂，用更少的符號(hào)個(gè)數(shù)就可以實(shí)現(xiàn)信道的估計(jì)。

圖2 信道誤差——符號(hào)個(gè)數(shù)

圖3 為各種重采樣算法在不同的信噪比下的信道估計(jì)。橫坐標(biāo)為信噪比，縱坐標(biāo)為信道的平均誤差。仿真條件：發(fā)送的比特?cái)?shù)為1 000，估計(jì)的粒子數(shù)為100，結(jié)果為仿真100次的平均值。從圖中可以看出，所提出的算法降序二分法在信噪比較低時(shí)就能完成對(duì)信道的估計(jì)，性能也明顯優(yōu)于其他三種重采樣算法。

圖3 不同信噪比下的信道誤差

圖4 不同信噪比下的誤碼率

圖 4為不同信噪比下的誤碼率。橫坐標(biāo)為信噪比，縱坐標(biāo)為誤碼率。仿真條件：發(fā)送的比特?cái)?shù)為5 000，估計(jì)的粒子數(shù)為100，結(jié)果為仿真100次的平均值。仿真結(jié)果表明，提出的算法比其他三種算法的盲均衡性能有所改善。

4 結(jié)語

提出了一種新的粒子濾波重采樣算法，這種算法將多項(xiàng)式重采樣算法和分層重采樣算法結(jié)合起來，主要思想是在分層重采樣算法的基礎(chǔ)上，尋找權(quán)重最大點(diǎn)的過程用折半二分法。把這種算法應(yīng)用于信道的盲均衡中，為了易于采樣，重要性函數(shù)采用先驗(yàn)概率密度，用信道的均值代替信道的真實(shí)值，仿真結(jié)果表明，這種算法的平均性能優(yōu)于之前的重采樣算法。

[1] GORDON N J, SALMOND D J, SMITH A F M. Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation[J].IEEE Proceeding-F,1993,140(02)：107-111.

[2] LIU J S,CHEN R. Blind Deconvolution Via Sequential Imputations[J]. American Statistical Association. 1995,90(430)：567-576.

[3] MíGUEZ J,DJURIC P M. Blind Equalization by Sequential Importance Sampling[C].USA：IEEE,2002：845-848.

[4] BERTOZZI T, LE Ruyet D, RIGAL G,et al. Joint Data-channel Estimation Using the Particle Filtering on Multipath Fading[C].French： French Polynesia Proceedings of ICT, 2003：1284-1289.

[5] BERTOZZI T, LE Ruyet D, RIGAL G,et al. On Particle Filtering for Digital Communications[M].USA：IEEE,2003.

[6] PUNSKAYA E, ANDRIEU C, DOUCET A,et al. Particle Filtering for Demodulation in Fading Channels with Non-Gaussian Additive Noise[J]. IEEE Transactions on Communication,2001(49)：579-582.

[7] 王磊，劉郁林，李正東. 粒子濾波理論及其在盲均衡中的應(yīng)用[J].重慶郵電學(xué)院學(xué)報(bào), 2005,17(06)：691-694.

[8] 王磊,劉郁林.基于粒子濾波的盲辨識(shí)和盲均衡新方法[J].通信學(xué)報(bào),2006,27(10)：131-135.