PSO-BP組合人工神經網絡算法研究

高峰

(山西大同大學工學院，山西大同037003)

PSO-BP組合人工神經網絡算法研究

高峰

(山西大同大學工學院，山西大同037003)

基于梯度下降的BP人工神經網絡應用廣泛，但網絡目標函數誤差曲面極其復雜，網絡初始值的選取對網絡訓練結果影響很大，導致收斂速度慢，容易陷入局部極小等問題.基于粒子群算法(pso)的訓練方法能夠擺脫陷入局部最優的困擾，但粒子群算法局部搜索能力不夠，影響網絡的訓練效果,在充分研究兩種算法特點的基礎上，提出一種新的組合訓練方法，建立了PSO-BP組合人工神經網絡模型.

組合人工神經網絡 BP算法 PSO算法 算法設計

人工神經網絡(ANN)以大腦生理研究成果為基礎，模擬生物神經網絡信息處理的網絡，是傳統工程系統與人工智能領域處理技術的混合，通過學習、記憶，采用類似黑箱方法擬合輸入變量與輸出變量間的非線性關系[1,2]，具有自學習、自組織、自適應能力和非局域性、非定常性、非凸性、非線性動態處理等特點，宜于表現多影響因子間的復雜因果規律,是求解非線性問題的常用方法.傳統BP網絡初始權值、閾值隨機設定，初值選取不當直接影響網絡收斂性能和最終穩定狀態，網絡學習易陷入局部極小，存在收斂速度慢、訓練時間長等問題，不能保證所優選權值為全局最優.

自然界中單個自然生物通常不是智能的，但卻有一定的群體行為，即整個群體表現出處理復雜問題的能力.基于對鳥群捕食行為研究和演化計算理論[4]的粒子群優化算法(PSO)，就是模擬自然生物行為的優化技術，具有記憶粒子最佳位置的能力和粒子間信息共享的機制，通過種群間內個體合作與競爭可實現優化問題求解.為克服傳統BP神經網絡缺陷，本文將PSO算法與BP神經網絡結合，建立PSO-BP組合人工神經網絡模型，以充分發揮PSO算法全局尋優能力和BP算法局部搜索優勢，縮短訓練時間，克服連接權值隨機問題.

1 BP-ANN理論

人工神經網絡(ANN)理論[1,2]是上世紀80年代中后期發展起來的非線性科學，在大腦神經網絡認識的基礎上，人工構造的能實現某種功能的神經網絡，是理論化的人腦神經網絡數學模型.ANN由許多神經元組成并行分布結構的信息處理網絡，顯示出人腦的某些基本特征，是傳統工程系統與人工智能領域處理技術的混合；它可從積累的工作經驗中學習知識，在數據含噪音、缺項或缺乏認知時能獲得較為滿意的結果，對于多變量系統，泛化能力強，能逼近任意非線性映射；高度并行計算能力使得容錯能力更高.

ANN模型結構是決定網絡特性的第二大因素，大量神經元按一定規則連接形成一定的拓撲結構,根據神經元連接方式與內部信息傳遞方向的不同，可分為前饋型神經網絡和反饋型神經網絡.ANN能進行復雜的邏輯操作和非線性映射，依賴于神經元間的相互作用，知識或信息存儲表現為網絡元件之間的分布式的物理聯系.生物神經元信息傳遞特性的數學表達式為：

式中，xi-輸入信號；wi-連接權值；Σ-信號累加；θ-神經元閾值；f-傳遞函數；Yi-輸出信號.

傳遞函數是神經元、神經網絡的核心，反映神經元輸出與激活狀態間的關系，決定了神經網絡求解問題的能力與效率，可分為閾值型傳遞函數、分段線性傳遞函數、非線性傳遞函數,見圖1.

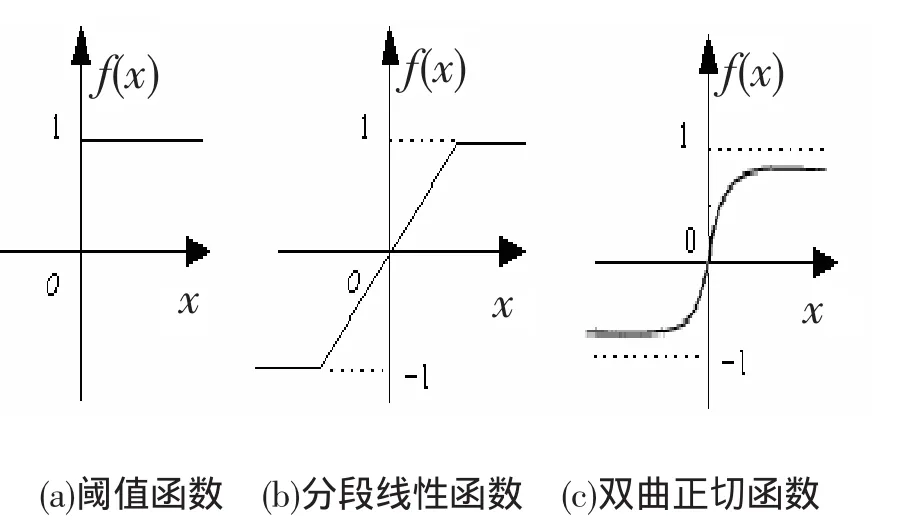
圖1 人工神經元中的傳遞函數

1.1 BP神經網絡原理

Ramelhart等提出的誤差反傳訓練(BP)算法[1,2]由正向計算和誤差反傳兩部分組成.BP神經網絡包含一個輸入層、一個輸出層及至少一個隱含層,見圖2.在網絡的正向計算中，輸入信息從輸入經隱含層逐層處理，并傳向輸出層，在正向傳播的過程中，每一層神經網絡的狀態只影響其下一層神經元的狀態.若輸出層不能得到期望的輸出，則轉入反向傳播，將輸出誤差沿原來的連接通路返回，通過修改各層神經元的權重，使最終的輸出誤差達到最小.

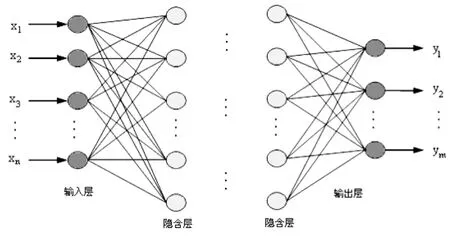
圖2 BP人工神經網絡模型結構

隱含層神經網絡是一組從輸入節點到輸出節點的高度非線性映射，BP累積誤差反向傳播算法步驟：①確定BP神經網絡結構；②設置權值、閾值矩陣、學習速率和動量因子;③學習訓練，直到誤差足夠小.BP算法數學意義明確、步驟分明，并具有中間隱含層和有相應的學習規則可循，使得它具有對非線性模式的識別能力，已成為工程應用最多、最成熟的方法之一.

1.2 BP人工神經網絡參數

1)神經網絡層數

Kolmogorov定理：任意連續函數f∶RT→Rm，f可以精確地用三層前饋網絡來實現.選擇合適神經元，神經網絡可任意精度逼近任一連續函數.增加層數可降低誤差、提高精度，但網絡趨于復雜，從而增加了網絡訓練時間[3],見圖3.因此，BP神經網絡設計時，一般設置一個隱層，先考慮增加隱含層神經元數,當節點數很多仍不能改善網絡性能時，才考慮增加隱層.

2)隱含層神經元數

較小規模網絡學習比較困難，適當增加神經元數目可提高誤差精度，訓練效果易于觀察和調整.但隱層節點數過多，節點冗余增加網絡訓練時間，模型泛化性能降低.通常可采用構造法、進化法、刪除法等確定隱層神經元數目.

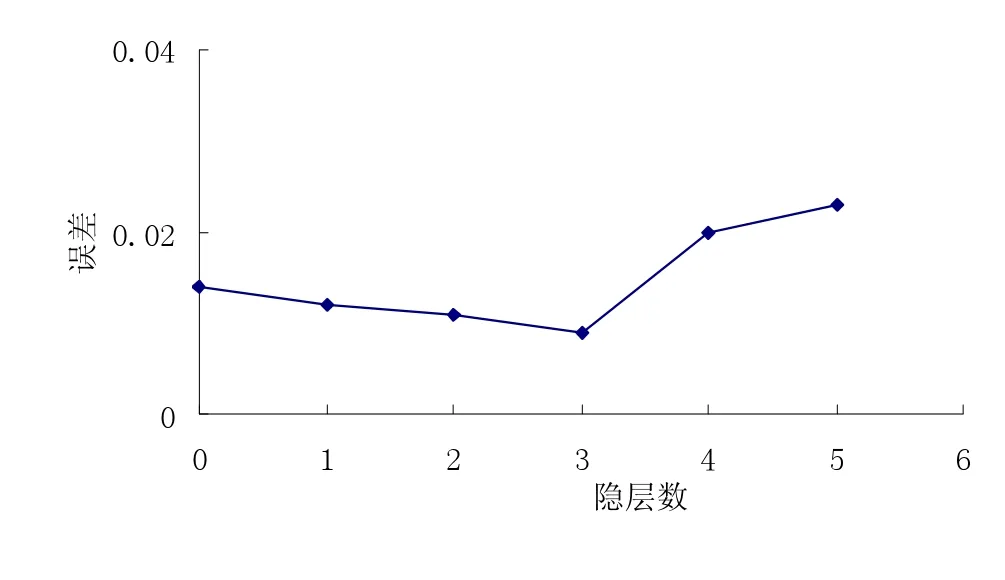
圖3 系統誤差-網絡隱層數變化曲線

3)初始權值

初始權值決定了非線性系統的收斂性及收斂速度.初值太大，使得加權后的輸入、輸出值落在S型傳遞函數飽和區，導數太小，導致計算權重修正值趨于0，從而使得調節過程幾乎停頓下來.因此，初始加權的神經元輸出值應近于零，以保證神經元權值在傳遞函數變化最大處調節，常取(-1，1)間的隨機數.

4)學習速率

學習速率決定每一循環訓練中權值變化量，值過大可導致系統不穩定，值過小雖能保證跳出網絡誤差表面低谷，趨于誤差最小值，但收斂速度慢，效率低.一般在[0.1,0.8]之間取值即可保證系統穩定性和精度要求.

2 粒子群優化算法

Reynolds研究鳥群飛行發現，鳥僅追蹤它有限數量的鄰居，但最終結果是整個鳥群好像在一個中心的控制下，即復雜的全局行為是由簡單規則的相互作用引起.一群鳥在隨機搜尋食物，若某區域里只有一塊食物，那么找到食物最簡單有效的策略就是搜尋目前離食物最近的鳥的周圍區域.

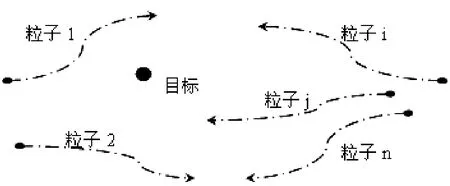
圖4 粒子群算法原理示意圖

Eberhart和Kennedy從中得到啟示，將鳥類尋找食物與特定問題尋找最優解聯系起來，用粒子(質量、體積忽略不記)來代替飛鳥，并為粒子制定類似于鳥類運動的簡單行為規則，從而使整個粒子群的運動表現出鳥類覓食的特性，即粒子最終能夠飛向解空間的最優解處[4-6],見圖4.

PSO求解優化問題時，解空間初始化為一群隨機粒子，每一粒子都有自己的位置、速度以決定飛行方向、距離，還有一個由被優化函數決定的適應值.各粒子記憶、追蹤當前的最優粒子，在解空間中搜索.在每次迭代中，粒子通過跟蹤個體極值、全局極值更新自己的速度、位置.粒子速度和位置更新方程為：

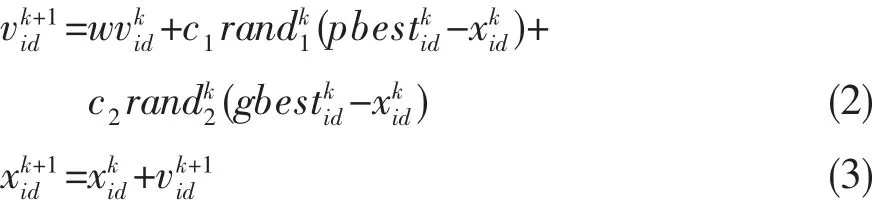
PSO算法采用速度-位移模型，避免了復雜的遺傳操作，特有的記憶使算法可動態跟蹤當前的搜索情況來調整其搜索策略，算法簡單有效，應用領域已擴展到多元函數與參數優化、模式識別、聚類分析、神經網絡等[4].

3 PSO-BP組合人工神經網絡算法

3.1 BP神經網絡與PSO融合

BP模型不需精確數學表達式，只要用已知模式對網絡加以訓練，網絡就具有輸入-輸出間的映射能力；理論基礎堅實、推導過程嚴謹、物理概念清晰、通用性強，廣泛應用于模式匹配、分類、自動控制等領域.但BP算法基于梯度下降算法，本質上屬局部尋優算法.復雜網絡的誤差曲面是一高維空間中的曲面，非常復雜和不規則，局部極小點多,見圖5，一旦陷入就很難逃脫出來，學習效果變差.

PSO算法以生物群體內通過個體間的合作與競爭所產生的群體智能為核心理論體系，屬于全局優化算法，具有收斂速度快，操作簡單、易于編程實現，是一種良好的優化算法.因此，引入粒子群算法對BP網絡初始權值和閾值等參數優化，可產生一種新的組合人工神經網絡模型.

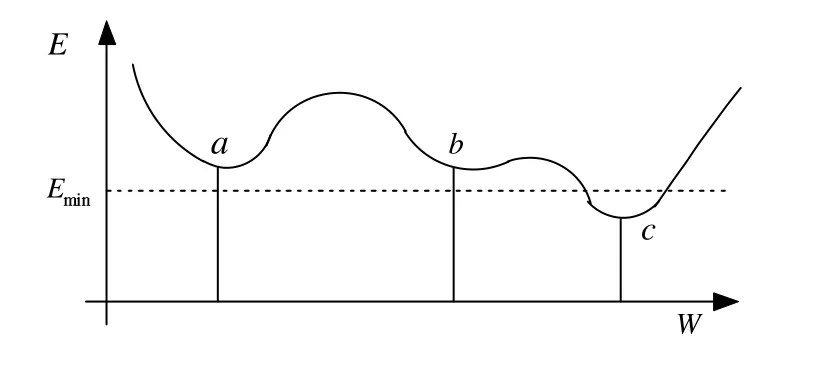
圖5 單權值調整過程中的局部極小點

PSO-BP神經網絡基本原理是，先將神經元間所有連接權值編碼成實數向量以表示種群中個體，隨機生成向量群體，迭代中新生成的個體向量還原為神經網絡權值，將訓練中產生的均方誤差作為評價個體的適應度函數，此時訓練轉化為尋找一組使均方誤差最小的最佳聯接權值優化問題.若均方誤差小于系統設定值或迭代次數大于最大迭代次數，則訓練過程停止；否則，迭代繼續進行，直至最大迭代次數，此時參數組合已較接近于最佳組合.然后，采用BP算法進一步精確優化上面得到的網絡參數，直至網絡參數最優.這樣既提高了神經網絡的學習能力，又增強了神經網絡泛化性能和預測能力.

3.2 PSO-BP組合人工神經網絡算法流程

PSO-BP組合神經網絡算法流程如下：

1)初始化BP神經網絡結構，設定網絡的輸入層、輸出層的神經元個數，設置網絡參數，通過試算確定最佳隱含層神經元個數.

2)初始化粒子群的規模、維度D以及每個粒子的初始速度、位置.種群規模一般取為10～40間的數值，復雜問題大于100；初始速度、位置可隨機賦值.問題解空間維度D計算公式：

式中，m、n、p、q分別為輸出層-隱含層連接權值個數、隱含層-輸出層連接權值個數、隱含層閾值個數、輸出層閾值個數.

3)根據適應度函數計算每個粒子的適應度方差，步驟為：

①按當前網絡結構和權值、閾值計算出每個樣本的輸出值.

②計算每個訓練樣本的輸出值的誤差.

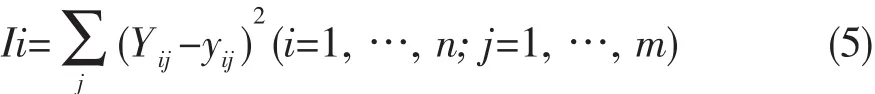
式中，n-訓練集樣本總數；m-輸出層神經元個數；Yij-實際輸出值；yij-理想輸出值.

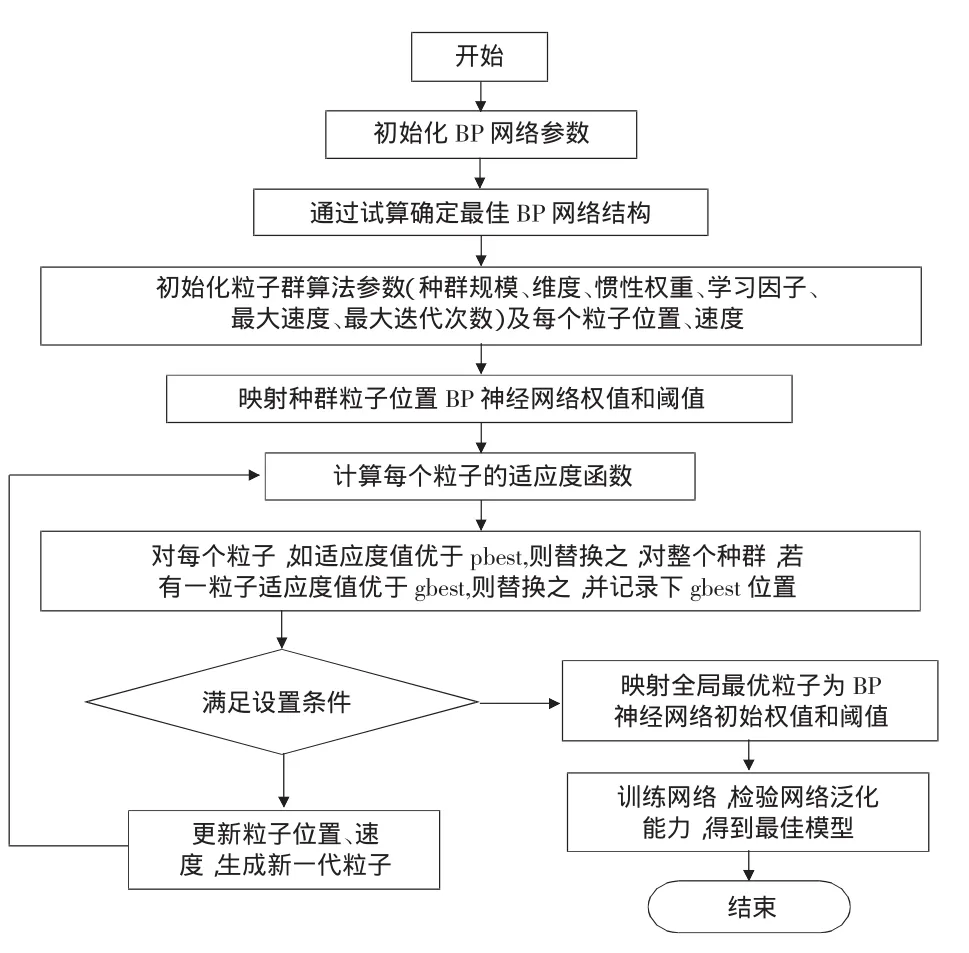
圖6 PSO-BP組合神經網絡運算流程

③計算出該粒子的適應度方差.

4)更新每一個粒子的個體極值、全局極值，生成下一代粒子.慣性因子w設計為隨迭代次數遞減，按照式(7)進行自適應調解.

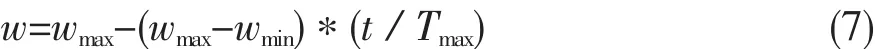
式中，wmax-最大慣性權重；wmin-最小慣性權重；t-當前迭代次數；Tmax-最大迭代次數.

5)檢查粒子適應度方差和當前最大迭代次數，若誤差大于系統設定值或迭代次數小于最大迭代次數，繼續步驟(3)進行下一代粒子計算；否則，退出迭代計算，將全局最優粒子位置映射為網絡初始權值和閾值,見圖6.

4 結論

BP算法非線性模式識別能力強大，但存在網絡學習易陷入局部極小，收斂速度慢、訓練時間長等問題.PSO算法以群體智能為核心理論體系，收斂速度快，操作簡單、易于編程實現，是一種很好的全局優化算法.基于粒子群算法建立的PSO-BP組合人工神經網絡模型，充分利用神經網絡的學習能力，發掘數據內隱藏的規律，為進一步拓展人工神經網絡應用領域開辟了一條新的途徑.

[1]張良均,曹晶,蔣世忠.神經網絡實用教程[M].北京:機械工業出版社,2008:12-45.

[2]徐秉錚,張百靈,韋崗.神經網絡理論與應用[M].廣州:華南理工大學出版社,1994:2-16.

[3]馮夏庭.智能巖石力學導論[M].北京:科學出版社,2000:102-145.

[4]Bonabean E,Dorigo M,Theraulaz G.Inspiration for optinization from social insect behavior[J].Nature,2000,406(6):39-42.

[5]曾建潮,介倩,崔志華.微粒群算法[M].科學出版社,2004:52-85.

[6]楊威,李岐強.粒子群優化算法綜述[J].中國工程科學,2004,6(5):87-90.

Abstract:BP artificial neural network based on gradient algorithm method is widely applied,but because the error surface of object function is extramly complex and the choose of initial value effects network training results,convergence rate is slow and local minimum is likely to fall into.Paticle swarm optimization algorithm has better global searching ability to get rid the puzzles of falling into local minimum.By adequately studying on the two algorithms'characteristics,a new type of combined artificial neural network training method is put forward,and PSO-BP ann model is successfully built.

Key words:combined artificial neural network;bp algorithm;pso algorithm;algorithm design

〔編輯 石白云〕

Research of PSO-BP Combined Artificial Neural Network Method

GAO Feng
(School of Engineering,Shanxi Datong University,Datong Shanxi,037003)

TP183；TU452

A

1674-0874(2010)03-0066-04

2010-04-12

高峰(1977-)，男，山東泰安人，講師，博士，研究方向:工程力學與巖土工程.