旋轉星座下極化準正交空時分組碼及性能分析

，沈連豐，王靜靜

（1. 東南大學 移動通信國家重點實驗室，江蘇 南京 210096；2. 揚州大學 信息工程學院，江蘇 揚州 225009）

1 引言

文獻[1]中提出了基于準正交設計的空時分組碼，文中的主要參數：碼率為1、發射天線數為4，但與正交設計相比較，系統性能有所降低。為了使準正交空時分組碼能夠取得滿分集，文獻[2]介紹了旋轉準正交空時分組碼，也就是對不同的發射符號選用不同的星座，前一半符號選用星座A，后一半符號選用A的旋轉星座，結論是對BPSK、QPSK和 8PSK系統最優的旋轉分別為π/2、π/4和π/8。文獻[3]介紹了能夠取得滿分集增益和滿碼率的旋轉準正交空時分組碼。文獻[4]介紹了四元素正交設計理論，并設計出了一些滿足正交設計的極化空時分組碼，該種分組碼可以通過極化天線進行發射和接收，與傳統正交空時分組碼相比，該碼可以降低系統誤碼率。文獻[5]根據完美空時分組碼的結構特點提出了等效的垂直—貝爾實驗室空時（V-BLAST）模型，并根據最小均方誤差—判決反饋均衡提出一種有邊界約束的Fano譯碼器，仿真結果表明了該譯碼器幾乎可達到最大似然譯碼性能。文獻[6]提出基于隨機旋轉的準正交空時分組碼的發射分集方法，這種方法對每個輸入信息符號序列進行隨機旋轉，使準正交空時分組碼的符號間干擾隨機化。文獻[7]構建了一種基于四元素準正交設計的空時分組碼，該種碼采用快速最大似然譯碼算法進行譯碼，最后與傳統準正交空時分組碼進行了性能仿真。

本文構建了碼率為3/4、發射天線數分別為8和 6的基于星座圖旋轉的極化準正交空時分組碼，該種碼采用雙極化天線進行發射和接收，對未旋轉—極化、旋轉—極化、未旋轉—傳統、旋轉—傳統這4種準正交空時分組碼進行了仿真比較。結果表明，在相同條件下，當采用雙極化天線時，星座圖旋轉對系統誤碼率性能改善不明顯；當采用單極化天線時，旋轉可以明顯改善系統誤碼率性能。

2 信道模型

考慮一個具有N個雙極化發射天線和一個雙極化接收天線的系統，信道模型如圖1所示。發射時隙數為T，接收信號向量表示為

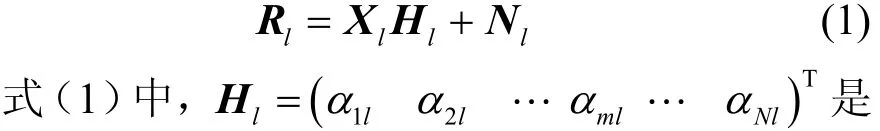
發射天線與接收天線之間的信道增益向量，維數為N× 1，其中l表示天線的極化方向，設1為水平極化、2為垂直極化，反之亦然，元素αml（m = 1 ,… ,N ;l= 1 , 2）是獨立同分布的復高斯隨機變量的抽樣，其實部和虛部的方差都為0.5；Xl是T×N維的發射碼字矩陣；是 T ×1維的噪聲向量，元素是獨立同分布的復高斯隨機噪聲，均值為 0，方差為1。

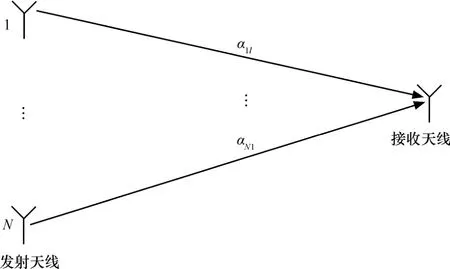
圖1 信道模型

3 準正交極化空時分組碼的設計

根據文獻[8]，一個碼率為3/4的正交空時分組碼為

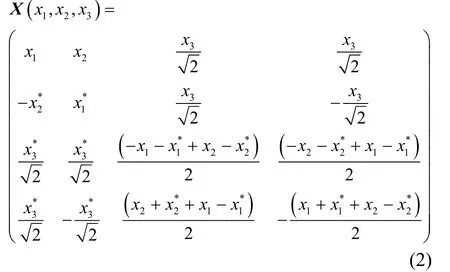
根據式（2）可以構造出一個發射天線數為8、碼率為3/4的準正交空時分組碼（T=N）。

其中，

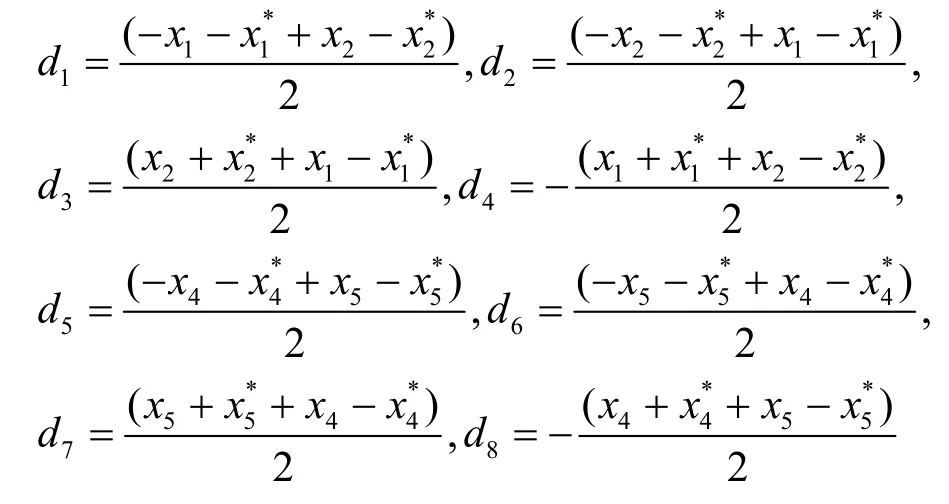
將X的第m列分別表示為 vm,m= 1 ,… ,8 ，則有

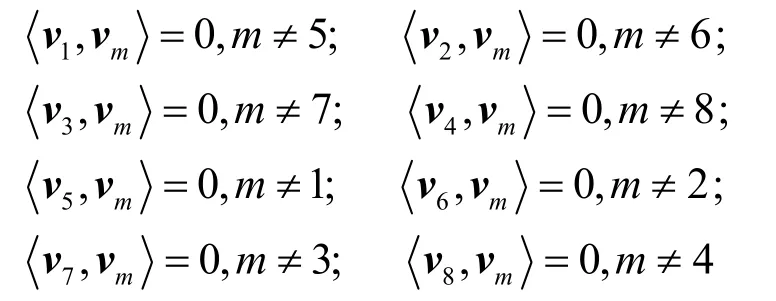
即滿足準正交關系。

根據式（3）構造出發射天線N=8、碼率為3/4的極化準正交設計空時分組碼為

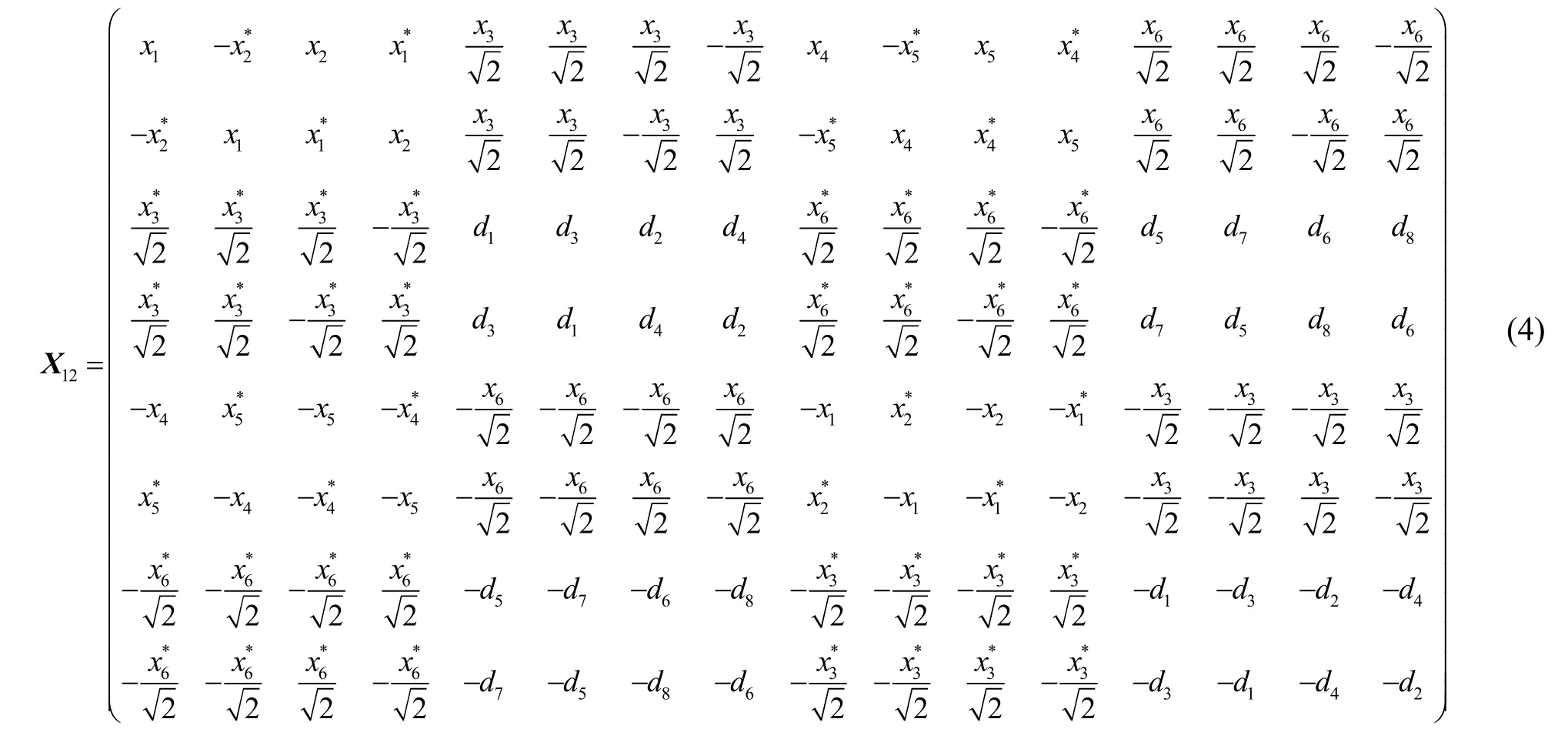
其中，奇數列表示通過雙極化發射天線水平極化方向發射的信號，而偶數列表示通過雙極化發射天線垂直極化方向發射的信號。X12中的1、2表示天線的極化方向，按奇數列和偶數列可以分解成 X1和X2，其中 X1為式（3）。

同理，根據文獻[1]可以設計出發射天線數為6、碼率為3/4的準正交碼字矩陣。

則可以得到 N=6時發射天線的極化準正交設計空時分組碼為

其中，奇數列表示通過雙極化發射天線水平極化方向發射的信號，而偶數列表示通過雙極化發射天線垂直極化方向發射的信號。星座圖旋轉就是x1,x2, x3不變，而 x4, x5, x6旋轉θ 角度，則式（4）和式（6）中 x,x,x旋轉θ 角度，變成 ejθx ,ejθx,

4564 5

ejθx6。

4 成對譯碼算法及增益分析

根據文獻[9]，對給定的碼字矩陣X和信道矩陣

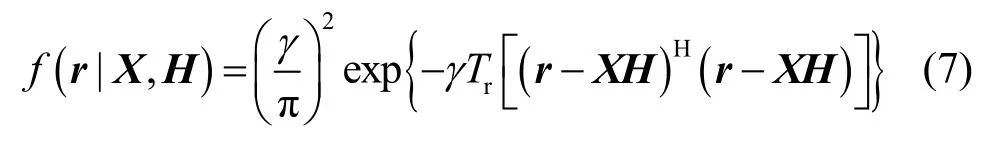
成對譯碼就是尋找碼字矩陣?X使式（7）概率密度函數最大，則式（7）可等價表示為：

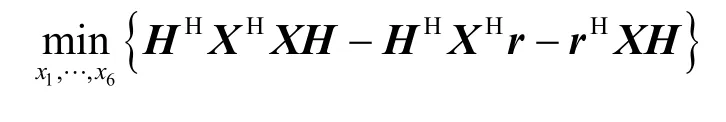
下面分2種情況進行分析。

1) N=8，沒有旋轉情況下的譯碼

對X1，水平極化方向的接收信號表示為

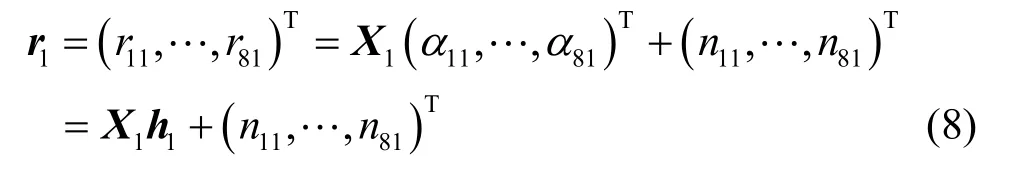
則

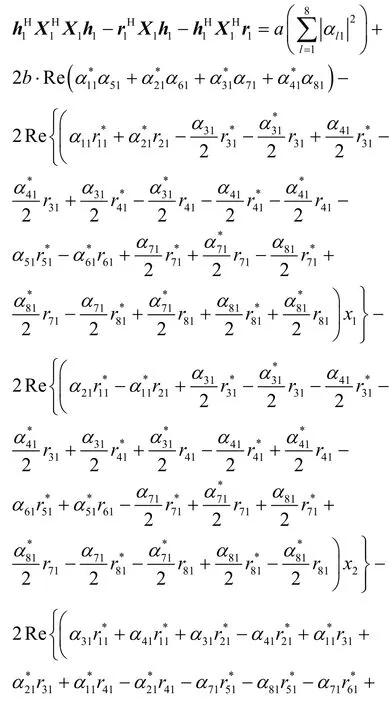
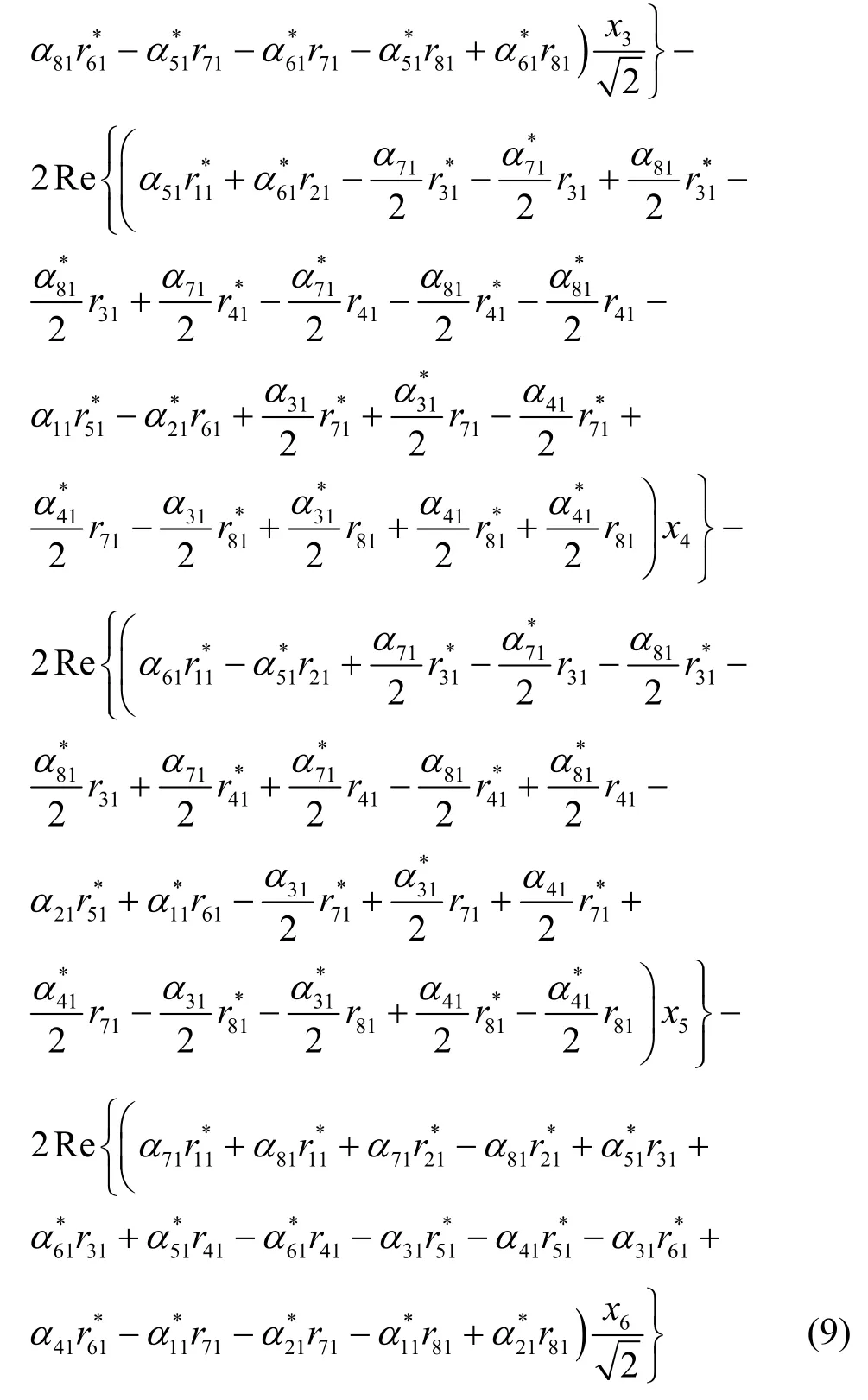
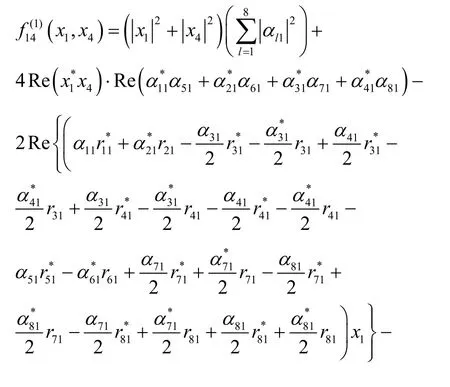
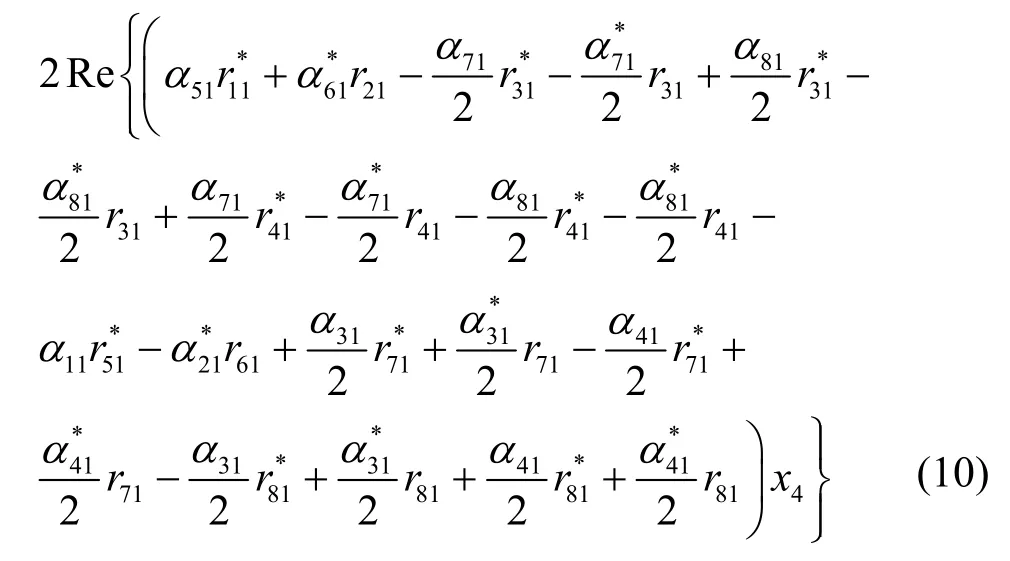
和

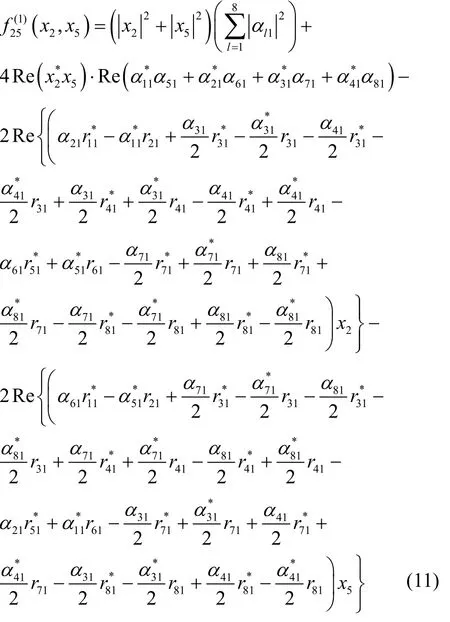
以及

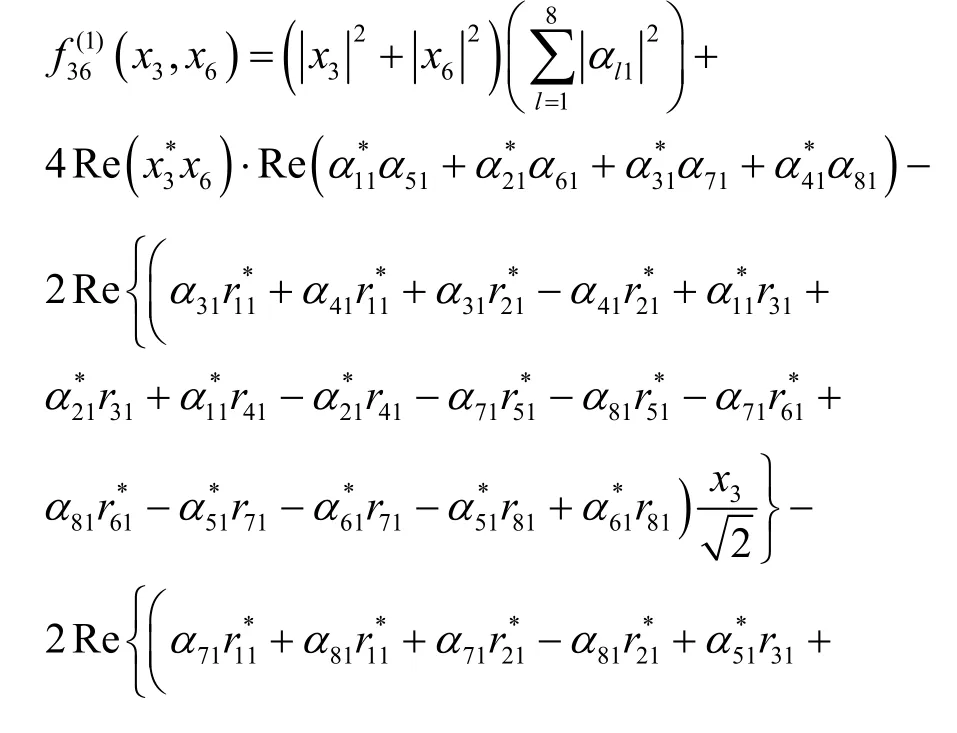
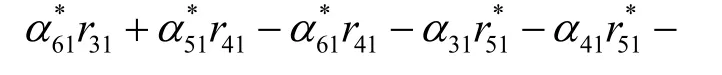
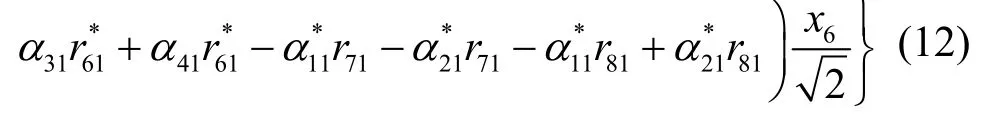
所以，接收端成對譯碼等價于分別最小化。

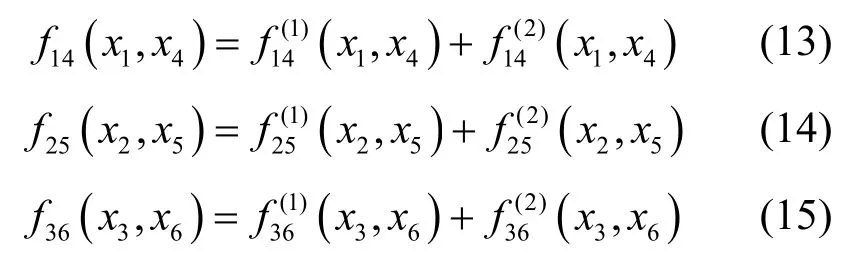
2) N=8，旋轉情況下的譯碼

x1,x2, x3沒有旋轉，而 x4, x5, x6旋轉θ角情況下的成對譯碼，此時上面各式中 x4,x5,x6分別變為和根據文獻[2]，BPSK、QPSK和8PSK的最佳旋轉角度分別為和

根據文獻[10]，定義2個碼字X1和X2的錯誤矩陣為，令2個碼字編碼增益距離（CGD, code gain distance）并用 dCG表示，有本文所設計碼字在未旋轉時，矩陣的秩為 2，旋轉后矩陣的秩為 3，故星座圖旋轉后可以達到滿分集增益。要獲得高的編碼增益，編碼增益距離的最小值必須較大，對 BPSK，QPSK和 8PSK，星座圖分別旋轉π/2、π/4和π/8時 d et(的最小值最大，即編碼增益最大。

N=6時，無旋轉和有旋轉情況下的分析方法與N=8時相同。

5 仿真及分析

仿真時發射端分別采用8個和6個雙極化發射天線，接收端采用1個雙極化接收天線，頻譜利用率分別為 0.75bit/(s·Hz)、1.5bit/(s·Hz)和 2.25bit/(s·Hz)，采用BPSK、QPSK和8PSK調制方式，星座圖分別旋轉π/2、π/4和π/8。仿真結果分別如圖2～圖7所示。

采用N=8個發射天線，由圖2～圖4可見，當BER=10-5、采用BPSK時，旋轉后極化空時分組碼的性能比未旋轉極化空時分組碼和旋轉傳統空時分組碼和未旋轉傳統空時分組碼分別提高約為0.2dB、4.5dB、5.6dB；采用QPSK時，對應的性能提高分別約為0.4dB、5dB、5.8dB；采用8PSK時，這種性能提高分別約為0.3dB、5.2dB、5.7dB。

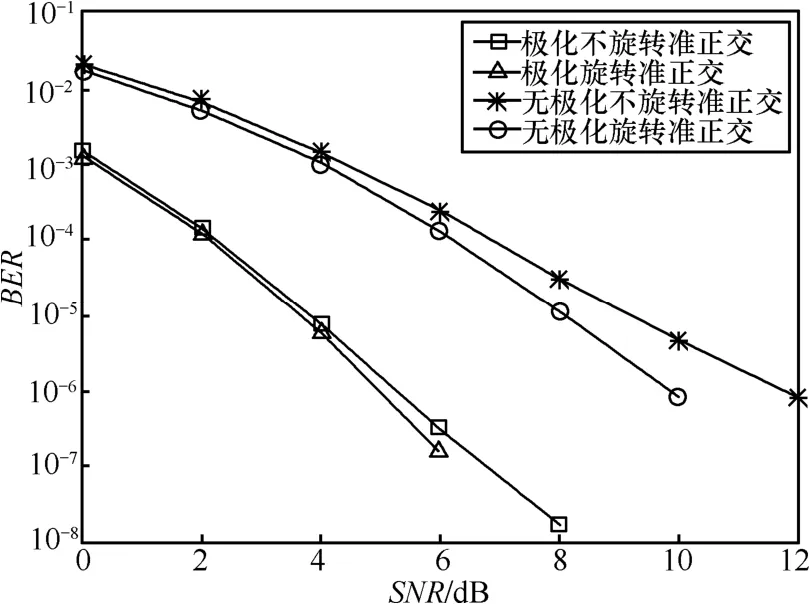
圖2 旋轉和未旋轉碼的性能比較（BPSK，0.75bit/(s·Hz)）N=8

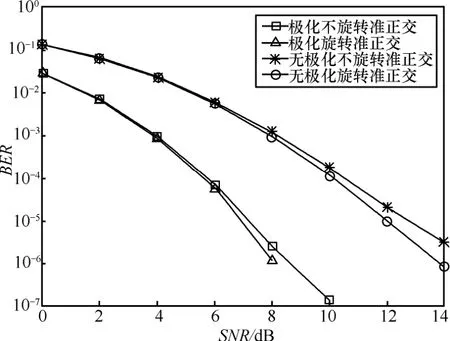
圖3 旋轉和未旋轉碼的性能比較（QPSK，1.5bit/(s·Hz)）N=8

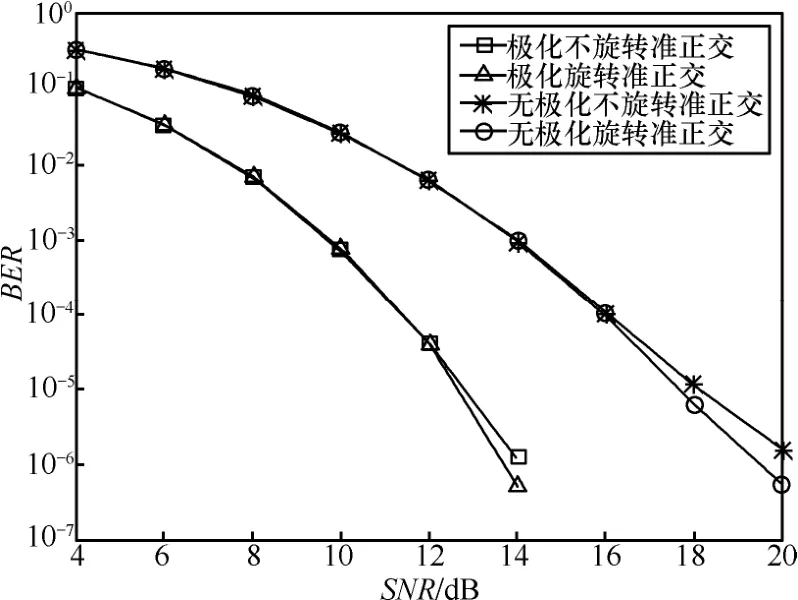
圖4 旋轉和未旋轉碼的性能比較（8PSK，2.25bit/(s·Hz)）N=8

采用N=6個發射天線，由圖5～圖7可見，當BER=10-5時，上述性能提高，分別約為0.3dB/5.5dB/7.3dB（BPSK）、0.4dB/5.6dB/7.5dB（QPSK）和0.2dB/6dB/7dB（8PSK）。

圖5 旋轉和未旋轉碼的性能比較（BPSK，0.75bit/(s·Hz)）N=6

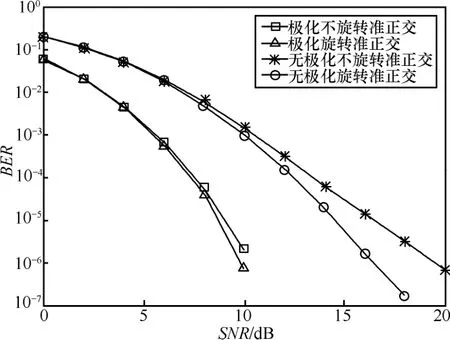
圖6 旋轉和未旋轉碼的性能比較（QPSK，1.5bit/(s·Hz)）N=6

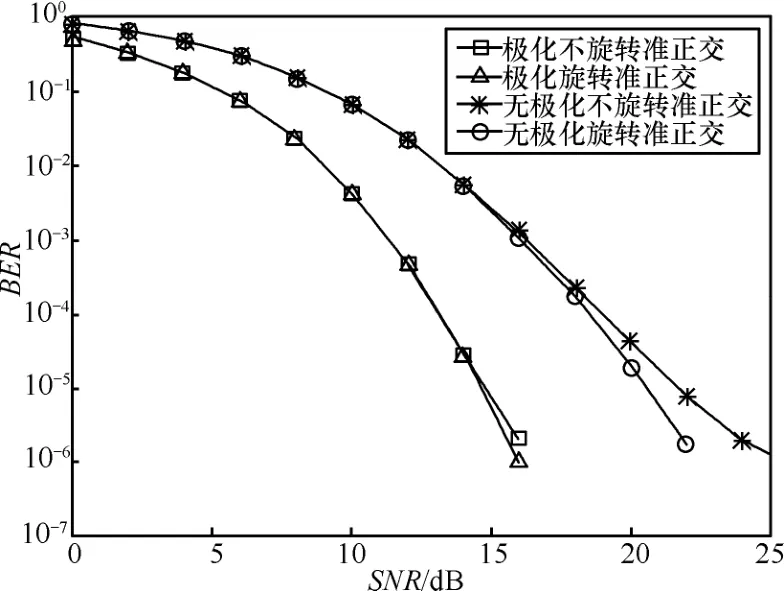
圖7 旋轉和未旋轉碼的性能比較（8PSK，2.25bit/(s·Hz)）N=6

由圖可知，與單極化天線相比，當采用相同數量（且數量較多）雙極化天線時，星座圖旋轉對系統誤碼率性能改善不明顯，這是因為采用較多雙極化天線發射信號時，在 SNR較低時誤碼率性能已經很好，即使對星座圖進行旋轉，改善也不是很明顯。當采用單極化天線發射信號時，在相同 SNR條件下，旋轉碼與未旋轉碼相比具有更低的誤碼率，可以明顯改善系統誤碼率性能。

6 結束語

本文設計了一種極化準正交空時分組碼，并對星座圖進行旋轉，接收機采用成對譯碼算法進行譯碼，在相同條件下，當采用雙極化天線發射時，旋轉碼與未旋轉碼相比系統誤碼率有適當改善，采用單極化天線時，旋轉后系統誤碼率有較明顯改善。

[1] JAFARKHANI H. A quasi-orthogonal space-time block code[J]. IEEE Trans on Communications, 2001, 49(1)∶ 1-4.

[2] SU W, XIA X G. Signal constellations for quasi-orthogonal space time block codes with full diversity[J]. IEEE Trans on Information Theory,2004, 50(10)∶ 2331-2347.

[3] SHARMA N, PAPADIAS C B. Improved quasi-orthogonal codes through constellation rotation[J]. IEEE Trans on Communications,2003, 51(3)∶ 332-35.

[4] SEBERRY J, FINLAYSON K, WYSOCKI T A, et al. The theory of quaternion orthogonal designs[J]. IEEE Trans on signaling processing,2008, 56(1)∶256-265.

[5] 胡軍鋒, 楊遠, 張海林. 完美空時分組碼及其高性能解碼算法[J].通信學報, 2007, 28(6)∶ 54-61.HU J F，YANG Y，ZHANG H L. Perfect space-time block codes and high performance decoding algorithm[J]. Journal of Communications,2007, 28(6)∶ 54-61.

[6] 鄧單, 朱近康. 基于隨機旋轉的準正交空時分組碼研究[J]. 電子與信息學報, 2006, 28(9)∶ 1626-1629.DENG D, ZHU J K. Study on random-rotation quasi-orthogonal space-time block code[J]. Journal of Electronics & Information Technology, 2006, 28(9)∶ 1626-1629.

[7] 李正權, 沈連豐, 許波. 基于四元素準正交設計的空時分組碼[J].東南大學學報(自然科學版), 2009, 39(2)∶ 191-196.Li Z Q, SHEN L F, XU B. Space time block code from quaternion quasi-orthogonal design[J]. Journal of Southeast University∶ Natural Science Edition, 2009, 39(2)∶ 191-196.

[8] TAROKH V, JAFARKHANI H, CALDERBANK A R. Space-time block codes from orthogonal designs[J]. IEEE Trans on Information Theory, 1999, 45(5)∶ 1456-1467.

[9] GUEY J C, FITZ M P, BELL M R, et al. Signal design for transmitter diversity wireless communication systems over Rayleigh fading channels[J]. IEEE Trans on Communications, 1999, 47(4)∶ 527-37.

[10] 哈米德·賈法哈尼著, 任品毅譯. 空時編碼的理論與實踐[M]. 陜西∶西安交通大學出版社, 2007.JAFARKHANI H. Space-Time Coding∶ Theory and Practice[M].Xi’an∶ Xi’an Jiatong University Press. 2007.