上海金屬期貨與現(xiàn)貨市場非對稱波動溢出效應(yīng)的實證研究

陳 鋒，高展軍

（西北政法大學(xué) 經(jīng)濟管理學(xué)院，西安 710063）

上海金屬期貨與現(xiàn)貨市場非對稱波動溢出效應(yīng)的實證研究

陳 鋒，高展軍

（西北政法大學(xué) 經(jīng)濟管理學(xué)院，西安 710063）

運用二維非對稱BEKK-GARCH模型，考察了上海金融期貨與現(xiàn)貨市場間收益率的非對稱波動溢出效應(yīng)。實證結(jié)果表明：樣本期鋁期貨與現(xiàn)貨收益率間存在雙向的波動溢出效應(yīng)，而銅期貨與現(xiàn)貨收益率波動溢出效應(yīng)不顯著；銅、鋁期貨、現(xiàn)貨市場間都存在雙向的波動非對稱效應(yīng)，都對來自對方市場的“消息”的沖擊有顯著的反應(yīng)。

波動溢出效應(yīng)、波動非對稱性、向量GARCH模型

1 研究方法

金融研究與實務(wù)領(lǐng)域，無疑更關(guān)注兩市場之間收益率條件均值的變動和相互作用，這也是本文研究的主要目的，因此需要建立多元GARCH模型來考察市場間波動溢出效應(yīng)。

Kraft，Engle(1983)提出了向量ARCH類模型，設(shè)一個維向量隨機序列：

在式（1）中，Mt為其均值向量，{εt}是一個 N×1 維向量隨機序列，且有εt|It-1～N(0,Ht),It-1是到t-1時刻的信息集，Ht是N×N維正定矩陣，且關(guān)于It-1是可測的。定義ht=Vech(Ht)，Vech（·）稱為向量半算子，表示把矩陣Ht的下三角陣按列依次堆積而成的N(N+1)/2維向量，向量GARCH類模型主要是研究Ht的不同動態(tài)特性。

此后，Bollerslev，Engle 和 Wooldridge（1988）提出擴展的向量GARCH模型中Vech(Ht)形式表示為：

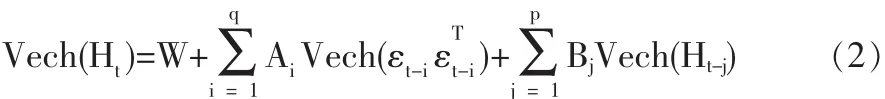
其中，W為N(N+1)/2維向量，Ai和 Bj均為[N(N+1)/2維方陣，且 Ai和 Bj使 Ht正定，i=1,2,3…p,j=1,2,3…q。

向量GARCH模型非常適合分析多市場之間的波動溢出效應(yīng)，模型參數(shù)矩陣Ai和Bj中的對角線元素反映方差、協(xié)方差序列自身的相關(guān)關(guān)系；而非對角線元素反映了不同變量的方差、協(xié)方差序列之間的相互影響，但向量GARCH模型的缺點參數(shù)過多，估計比較困難，而且實際運用中很難保證Ht正定。

Engle 和 Kroner(1995)在綜合 Baba，Engle，Kraft和 Kroner的研究基礎(chǔ)上提出了一種實施正定限制的參數(shù)化模型，簡稱為BEKK-GARCH模型，其模型表示如下：

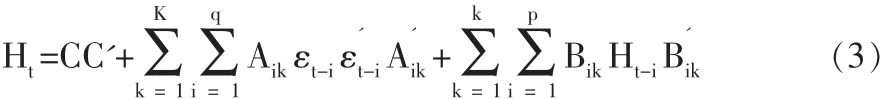
式（3）中，Aik和 Bik為 N 維方陣，C 是[N(N+1)/2]的上三角陣，當(dāng)K=P=q=1，簡化的BEKK-GARCH(1,1)模型可以表示為式（4）：

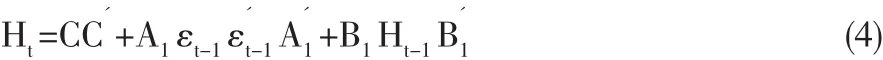
BEKK-GARCH模型的優(yōu)點是容易滿足Ht的正定，待估計的參數(shù)也相對較少，但模型中參數(shù)的經(jīng)濟學(xué)涵義相比于向量GARCH模型不夠明確。在式(4)BEKK模型中往往假設(shè)殘差項εt服從多元正態(tài)分布，而現(xiàn)實中金融時間序列往往呈現(xiàn)“尖峰厚尾”的特征，并不能完全服從正態(tài)分布，t分布或廣義誤差分布（GED）相比正態(tài)分布能更好的反映序列的“尖峰厚尾”的特征。

Kroner和Ng(1998)在BEKK-GARCH模型的基礎(chǔ)上，提出包含一般動態(tài)協(xié)方差的非對稱BEKK模型（Asymmetric BEKK）。 令 ηit=max[0,-εit]和 ηt=[η1t…ηNt]，則非對稱 BEKK 模型可以被定義為式（5）的形式：

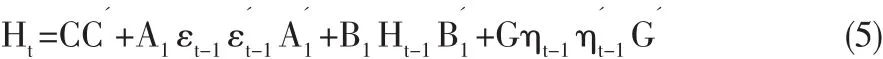
其中，G為N維方陣，且ηit為負(fù)值，代表了壞消息對Ht產(chǎn)生的沖擊影響，只需G方陣中所有元素顯著不為0，就說明存在著非對稱的杠桿效應(yīng)。

國外文獻(xiàn)中BEKK-GARCH模型的運用主要有：Karolyi(1995)使用BEKK-GARCH模型估計了美國和加拿大股票市場收益率間的波動關(guān)系；Kearney and Patton(2000)運用BEKK-GARCH模型分別估計了三個、四個和五個匯率市場間的波動溢出效應(yīng)；Worthington和Higgs(2004)運用BEKKGARCH模型檢驗了亞洲市場間的波動溢出關(guān)系；都取得了良好的估計效果，國內(nèi)文獻(xiàn)中主要在對中國股票市場研究中介紹或使用過該模型，期、現(xiàn)貨市場間波動性研究尚沒有文獻(xiàn)涉及。

本文目的是考察上海金屬期貨與現(xiàn)貨市場間的波動性關(guān)系，建立二維的非對稱BEKK-GARCH模型，參數(shù)方陣Aik、Bik和Git中，令i=1,2，其中1代表現(xiàn)貨市場，2代表期貨市場。二維非對稱BEKK-GARCH模型的展開式可以表示為下面（6）式的形式，其中對角線參數(shù)反映各市場自身的相關(guān)關(guān)系；非對角線參數(shù)（a12,a21）、（b12,b21）反映期貨與現(xiàn)貨兩市場間的波動溢出效應(yīng)；（g12,g21）反映期貨與現(xiàn)貨兩市場間的波動非對稱性。本文考察重點是上海金屬期、現(xiàn)貨兩個市場間的溢出效應(yīng)，我們將針對模型參數(shù)方陣中非對角線元素的非線性組合進(jìn)行似然比LR統(tǒng)計量和Wald統(tǒng)計量的檢驗。對上海鋁、銅期、現(xiàn)貨市場之間的波動溢出效應(yīng)作如下檢驗：

（1）原假設(shè) H0:a12=b12=0,a21=b21=0，不存在期貨與現(xiàn)貨市場間雙向的波動溢出效應(yīng)；

（2）原假設(shè)H0:a12=b12=0，不存在現(xiàn)貨市場對期貨市場的單向波動溢出效應(yīng)；

（3）原假設(shè)H0:a21=b21=0，不存在期貨市場對現(xiàn)貨市場的單向波動溢出效應(yīng)；

（4）原假設(shè)H0:g12=g21=0，不存在期貨與現(xiàn)貨市場間雙向的波動非對稱效應(yīng)；

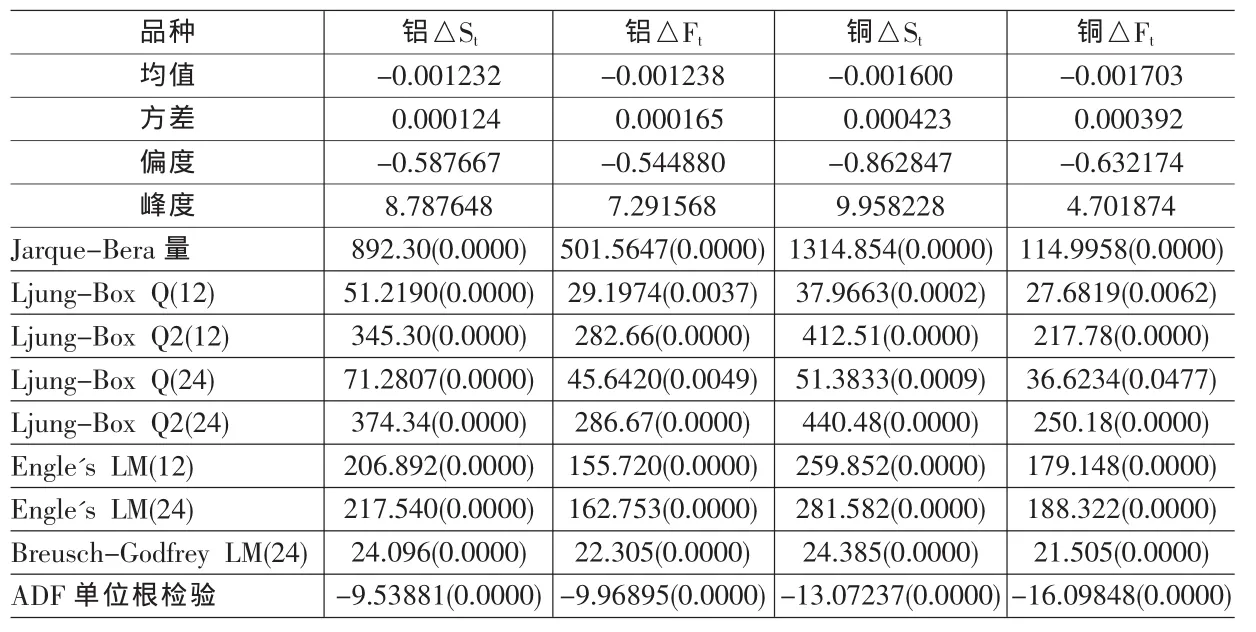
表1 描述統(tǒng)計、ARCH效應(yīng)檢驗結(jié)果

2 數(shù)據(jù)說明與ARCH效應(yīng)檢驗

2.1 數(shù)據(jù)說明

本文研究數(shù)據(jù)選取上海期貨交易所鋁連續(xù)、銅連續(xù)合約日收盤價，以及對應(yīng)期間上海有色金屬市場鋁、銅現(xiàn)貨的日價格。鋁期貨與現(xiàn)貨數(shù)據(jù)樣本期為2006年5月18日至2008年12月9日，共計近30個月615個交易日；銅期貨與現(xiàn)貨數(shù)據(jù)樣本期為2006年5月30日至2008年12月9日，共計近30個月615個交易日；數(shù)據(jù)來源于長江有色金屬市場網(wǎng)站歷史數(shù)據(jù)資料和彭博期貨行情軟件。交易日的現(xiàn)貨價格與期貨收盤價，那么現(xiàn)貨日收益率與期貨日收益率則分別St為Ft與的一階差分，表示為△St與現(xiàn)貨市場的價格序列定義為St=Ln(Pt)，期貨市場的價格序列定義為其中分別是第 t個△Ft，即△St=Ln(Pt/Pt-1)，

2.2 描述性統(tǒng)計和ARCH效應(yīng)檢驗

分別對鋁、銅現(xiàn)貨、期貨市場日收益率序列進(jìn)行描述性統(tǒng)計分析，和收益率序列自相關(guān)的Ljung-BoxQ統(tǒng)計量檢驗、Engle拉格朗日乘數(shù)（LM）檢驗、Breusch-Godfrey LM高階序列相關(guān)檢驗方法，來檢驗收益率殘差的方差是否存在條件異方差，并且對序列進(jìn)行平穩(wěn)性的ADF檢驗，結(jié)果見表1：

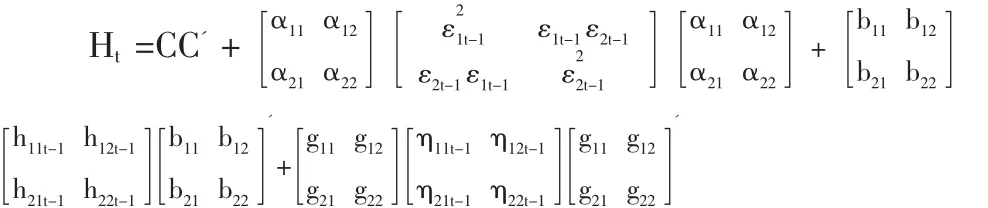
從表1結(jié)果可知，在樣本期，鋁期貨市場的方差大于現(xiàn)貨市場，表明鋁期貨市場價格波動程度大于現(xiàn)貨市場，而銅市場正好相反，銅現(xiàn)貨市場價格波動程度大于期貨市場；鋁、銅現(xiàn)貨、期貨市場從偏度來看，均為左偏的，銅市場的偏度較大；從峰度來看,鋁、銅現(xiàn)貨、期貨市場的峰度均大于3，Jarque-Bera統(tǒng)計量均奇大，說明鋁、銅現(xiàn)貨、期貨市場均呈現(xiàn)“尖峰厚尾”的分布，并不能完全符合正態(tài)分布。Ljung-Box Q、Engle LM、Breusch-Godfrey LM檢驗統(tǒng)計量的概率值均顯著為0，說明鋁、銅現(xiàn)貨、期貨市場收益率的殘差序列均存在條件異方差，即收益率的波動具有隨時間推移而改變的自回歸條件異方差（ARCH）現(xiàn)象，而且ADF單位根檢驗鋁、銅市場日收益率序列均為平穩(wěn)序列，適宜于建立ARCH族模型進(jìn)行分析。

3 實證結(jié)果

上海鋁、銅現(xiàn)貨、期ARCH效應(yīng)，建立非對稱向量BEKK-GARCH(1,1)模型進(jìn)行實證分析，檢驗現(xiàn)貨收益率與期貨收益率間的波動溢出效應(yīng)是否存在，以及波動溢出是否呈現(xiàn)非對稱性。本文采用無約束最貨市場收益率均具優(yōu)化BFGS（Broyden，F(xiàn)letcher，Goldfarb 和 Shanno）算法來估計使模型似然值極大的參數(shù)向量，分別正態(tài)分布、t分布和廣義誤差分布（GED）的假設(shè)下，并依據(jù)AIC值最小準(zhǔn)則選擇最優(yōu)模型。表2為式(6)的估計結(jié)果，包括收 益率波動的持續(xù)性、自身波動的非對稱性、波動溢出效應(yīng)、波動的非對稱性等信息，表3為兩市場之間波動溢出及波動的非對稱效應(yīng)檢驗結(jié)果。由表2和表3可得：

（1）從鋁、銅現(xiàn)貨、期貨市場收益率序列自身波動看，即式（6）中Aik、Bik的對角線元素，僅鋁期貨前一期誤差項不顯著，其余各參數(shù)均在1%置信水平下顯著，說明各序列自身波動有明顯的持續(xù)性；現(xiàn)貨、期貨市場間，在式（6）Aik中的非對角線元素，只有鋁現(xiàn)貨與期貨市場間具有波動的持續(xù)性。

（2）從收益率序列自身波動的非對稱性看，即式（6）中的gik對角線元素，除鋁現(xiàn)貨外，其余均顯著性，說明鋁現(xiàn)貨不存在“熱波”效應(yīng)，即鋁現(xiàn)貨市場對前一期的“消息”的沖擊沒有明顯反應(yīng)；鋁期貨、銅現(xiàn)貨和銅期貨估計系數(shù)均顯著不為0，說明從自身收益率序列看，存在波動非對稱的杠桿效應(yīng)，即對各自市場前一期的“消息”沖擊有明顯反應(yīng)；

（3）從現(xiàn)貨與期貨收益率間的波動溢出效應(yīng)來看，即式（6）中Bik的非對角線元素，鋁現(xiàn)貨與期貨估計系數(shù)在1% 顯著水平下均顯著，說明鋁現(xiàn)貨與期貨市場間具有顯著雙向跨市場波動溢出效應(yīng)，既具有“流星雨”效應(yīng)；而銅市場估計系數(shù)均不顯著，說明銅現(xiàn)貨與期貨收益率變動波動性沒有顯著的跨市場波動溢出效應(yīng)。

（4）從現(xiàn)貨與期貨市場間波動非對稱性方面看，即式（6）中g(shù)ik的非對角線元素，在鋁市場估計系數(shù)均顯著不為0，鋁現(xiàn)貨、期貨市場間均具有波動的非對稱性，說明在鋁現(xiàn)貨、期貨市場都對來自對方市場的“消息”有明顯反應(yīng)；在銅市場估計系數(shù)也均顯著不為0，說明銅現(xiàn)貨、期貨市場間雖沒有顯著的波動溢出效應(yīng)，但市場間卻存在著顯著的波動非對稱效應(yīng)，這一點與Koutmos和Tucker(1996)等人的研究結(jié)論相似。

4 結(jié)論和未來研究的建議

本文樣本期處于“大熊市”時期，期間又爆發(fā)了美國“次貸”危機引發(fā)的金融“大海嘯”，對國際金屬市場產(chǎn)生重大影響，在此背景下并結(jié)合國外學(xué)者及華仁海、劉慶富、張金清等國內(nèi)學(xué)者的相關(guān)文獻(xiàn)分析如下：

（1）本文結(jié)論上海銅市場間的波動溢出效應(yīng)不顯著，與張金清(2006)、劉慶富(2007)的研究結(jié)論不相符，本文樣本期間位于兩人研究期間之后，說明上海銅期貨與現(xiàn)貨存在顯著的雙向波動溢出效應(yīng),而銅市場間則不顯著,我們認(rèn)為這并不能作為比較兩市場成熟程度的依據(jù),兩市場這樣的差異,可能與兩種金屬在中國的儲藏量、生產(chǎn)量的差異有關(guān)，這種差異的存在，造成兩市場所受到的影響信息來源上存在不同。結(jié)合華仁海（2005），張金清（2006）、劉慶富（2008）的研究結(jié)論，可能與銅期貨市場的國際化市場間，收益率的波動溢出效應(yīng)并不是始終存在，不具有一貫性，可能會隨市場情況的變化而發(fā)生變化，正如Gwilym and Buckle(2001)所指出市場景氣循環(huán)也是收益率波動效應(yīng)的重要決定因素；也可能如Min和Najand.(1999)D對韓國KOSPI(200)指數(shù)期、現(xiàn)貨市場的研究發(fā)現(xiàn)市場間波動溢出效應(yīng)存在顯著的樣本依賴。

表2 非對稱波動溢出效應(yīng)估計結(jié)果

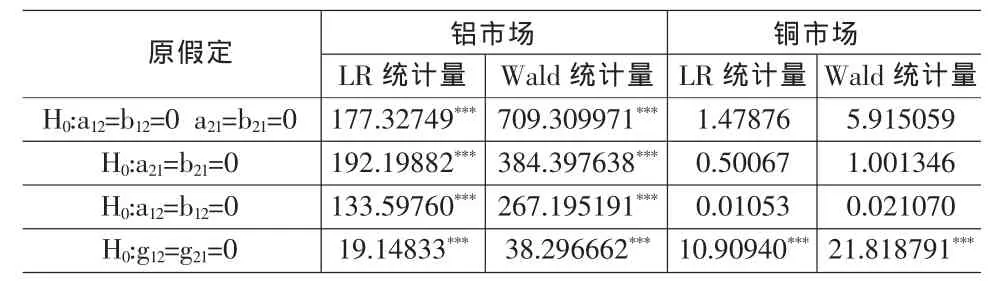
表3 期、現(xiàn)貨兩市場之間波動溢出及波動的非對稱效應(yīng)檢驗

（2）在樣本期的“大空頭”市場，上海鋁、銅期貨、現(xiàn)貨市場間波動溢出效應(yīng)表現(xiàn)不同，鋁期貨與現(xiàn)貨市場間程度相對較高有關(guān)。

（3）上海金屬期貨與現(xiàn)貨市場間存在顯著的波動非對稱性的杠桿效應(yīng)，這一點與張金清(2006)、劉慶富(2007)的結(jié)論相符，在“大熊市”和國際金融危機的雙重打擊下，期、現(xiàn)貨兩市投資者都對來自對方市場的信息有著敏感的反應(yīng)，但實證結(jié)果并不能解釋銅市場間的波動非對稱效應(yīng)的產(chǎn)生機理，可能與上海銅期貨、現(xiàn)貨市場分別受到國際銅期貨、現(xiàn)貨市場的較強影響有關(guān)。

（4）本文以及國內(nèi)相關(guān)文獻(xiàn)實證研究中，還存在著沒有考慮收益率序列均值樣本期在不同域之間變化的問題，忽略域變特點可能會造成波動性測量值相對于真實值出現(xiàn)偏差，從而影響實證結(jié)論的精確程度。因此有關(guān)中國期、現(xiàn)貨市場間波動性的研究還有待進(jìn)一步的深入。

[1]Black,F.Studies of Stock Markets Volatility Changes,Proceedings of the American Statistical Association[C].Business and Economic Statistics Section,1976.

[2]Stephen A.Ross.Information and Volatility:The No-Arbitrage-Martingale Approach to Timing and Resolution Irrelevancy[J].The Journal of Finance，1989,44(1).

[3]Robert F.Engle,Takatoshi Ito,Wen-Ling Lin.Meteor Showers or Heat Waves?Heteroskedastic Intra-Daily Volatility in the Foreign Exchange Market[J].Econometrica,1990,58(3).

[4]Chui-Chun Tsai,Tsun-Siou Lee.An Investigate on Information Transmission ofNearby-Month Taiwan Stock Index Futures during Trading,Nontrading,and between Trading and Nontrading Period:Price Discovery and Content of Price Volatility[J].Journal of Financial Studies,2004,12(1).

[5]Koutmos,G.,Tucker M.Temporal Relationships and Dynamics Interactions between Spot and Futures Stock Markets[J].Journal of Futures Markets,1996,16(1).

[6][臺灣]蔡垂君,李存修.臺灣股價指數(shù)與指數(shù)期貨跨市場價量訊息傳遞關(guān)系之實證研究-價格發(fā)現(xiàn)與價量關(guān)系[J].中華管理評論(國際學(xué)報),2004,7(2).

[7]Angelos.Kanas.Volatility Spilloversbetween Stock Returnsand Exchange Rate Changes:International Evidence[J]..Journal of Business Finance&Accounting,Blackwell Publishing,2000,27.

[8]華仁海,劉慶富.國內(nèi)外期貨市場之間的波動溢出效應(yīng)研究[J].世界經(jīng)濟,2005,(8).

[9]張金清,劉慶富.中國金屬期貨市場與現(xiàn)貨市場之間的波動性關(guān)系研究[J].金融研究，2006,(7).

[10]劉慶富,仲偉俊.我國金屬期貨與現(xiàn)貨市場之間的價格發(fā)現(xiàn)與波動溢出效應(yīng)研究[J].東南大學(xué)學(xué)報(哲學(xué)社會科學(xué)版),2007,(5).

[11]R F Engle,KF Kroner.Multivariate Simultaneous Generalized ARCH[J].Econometric Theory,1995,11.

[12]張世英,樊智.協(xié)整理論與波動模型——金融時間序列分析及應(yīng)用[M].北京:清華大學(xué)出版社,2004.

(責(zé)任編輯/易永生）

F724.5

A

1002－6487（2010）17－0150-03