The Automorphism Group of the Schr?dinger-Virasoro Lie Algebra＊

GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

The Automorphism Group of the Schr?dinger-Virasoro Lie Algebra＊

GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

To study the structure of the Schr?dinger-Virasoro Lie algebrasv,we characterize the structure of the automorphism groupA ut(sv)ofsvby calculating the automorphisms ofsvand determining the relationships between certain subgroups generated by some special automorphisms.

Virasoro algebra;Schr?dinger-Virasoro algebra;automorphism

CLC number:O152.5Document code:AArticle ID:1009-1734(2010)01-0006-05

MSC 2000:08A35

0 Introduction

The Schr?dinger Lie algebra plays an important role in mathematical physics and its applications. The Schr?dinger Lie algebra inddimensions,denoted byscd,has a basis

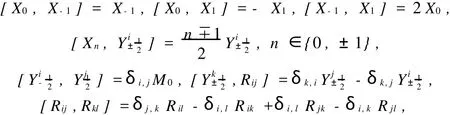
and others vanish.scdis(d2+d+4)-dimensional with 1-dimensional centerCM0and a 3-dimensional simple Lie subalgebra sl(2,C)generated byX-1,X0,X1.The Schr?dinger Lie algebra has attached considerable interest since it was introduced and investigated as the algebra of symmetries of the free Schr?dinger equation[2～3].Its structure and representations have been extensively studied[4～5].

In[1],M.Henkel firstly introduced Schr?dinger-Virasoro Lie algebrasvduring his study on the invariance of the free Schr?dinger equation.svis a vector space over the complex fieldCwith a basis

for allm,n∈Z.It is easy to see thatsvis a semi-direct product of the centerless Virasoro algebraW= span{Ln|n∈Z}and the two-step nilpotent infinite-dimensional Lie algebrah=span{Mn,|n∈Z},Henkel investigated that sv has one-dimensional universal central extension.C.Roger and J.Unterberger studied the structure and representation theory ofsvin[6].They presented a detailed cohomological study and determinedsvhas three outer derivations.But the automorphism group ofsvhas not beenworked out.Recently,extensions and generalizations related to the Schr?dinger-Virasoro algebra have appeared and their structure and representation theory have been extensively studied,such as[7],[8].

In this paper,we determine the structure of the automorphism groupA ut(sv)of the Schr?dinger-Virasoro algebrasv.Throughout the paper,we denote byZandC＊the set of integers and the set of nonzero complex numbers respectively,and all the vector spaces are assumed over the complex fieldC.

1 The Automorphism GroupAut(sv)

TheSchr?dinger-VirasoroLiealgebrasvisaperfectLiealgebrawithfinitegenerators

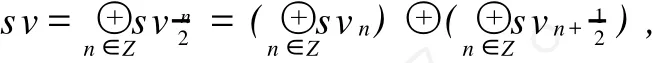
wheresvn=span{Ln,Mn}and=span{}for alln∈Z.

Denote byA ut(sv)andIthe automorphism group ofsvand the inner automorphism group ofsvrespectively.Obviously,Iis generated by{exp(kadMm+lad Y),m,n∈Z,k,l∈C}.For convenience, set

NoteCM0,MandM+Yare all non-trivial proper ideals ofsv,then it is easy to deduce the following lemma.

lemma 1.1 For allσ∈A ut(sv),we have

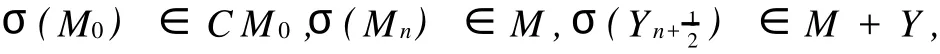
for alln∈Z.

LetJbe a subgroup ofIgenerated by{exp(k ad Mn)|n∈Z,k∈C}.ThenJis an abelian normal subgroup ofI.As a matter of fact,Jis the center of the groupI.

For alli,j,k∈Z,it is easy to see that

Consequently,we can deduce that

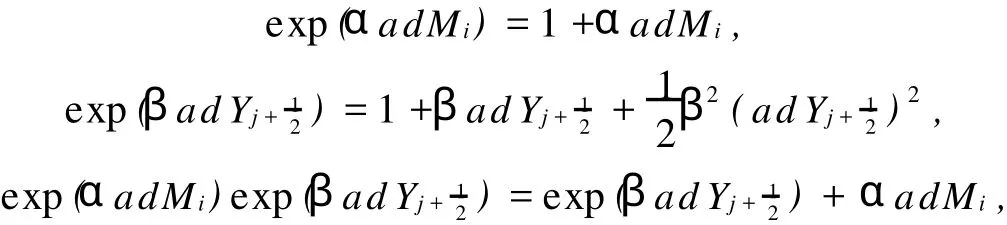
for allα,β∈C.Furthermore,we get

for allmk∈Z,bmk∈C,1≤k≤t.

lemma 1.2 For anyσ∈A ut(sv),there exist someτ∈Iandε∈{±1}such that

Proof By the automorphism group of the classical Witt algebra[9],there exists someε∈{±1}such that

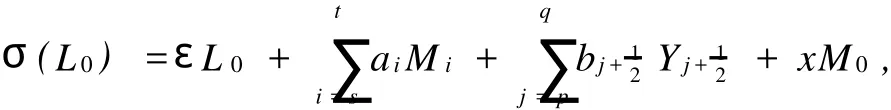
wherei≠0 andk+l+1≠0.Obviouslyτ,∈I.Note that for anyθ∈I,we haveθ(Mn)=Mnfor alln∈Z. By direct calculation,we obtain

wherei≠0 andy∈C.Setσ=τ-1σ,then there exists somea0∈Csuch that

By Lemma 1.1 and the automorphism group of the classical Witt algebra,we can assume that

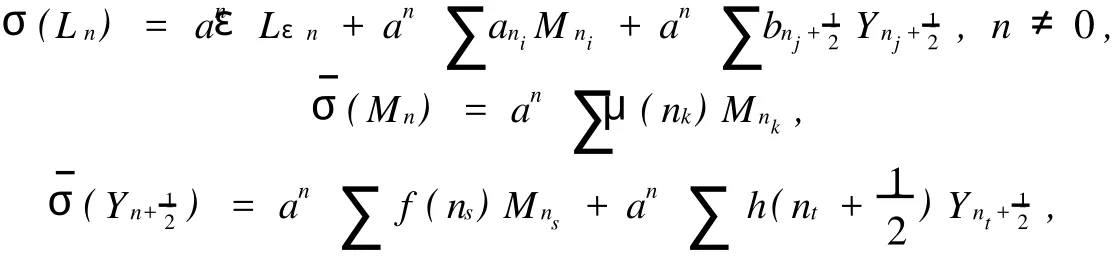
where each formula is of finite terms andμ(nk)∈C＊,ani,bnj+12,f(ns),h(nt+12)∈C＊.From the relation that[σ(L0),σ(Lm)]=mσ(Lm),we have

Thenni=εnforani≠0 andbnj+12=0 for allj.So

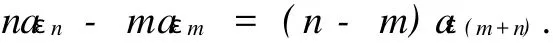
Letm=1,thennaεn-aε=(n-1)aε(n+1).By induction onn∈Z,we can infer that

Since[σ(L0),σ(Mn)]=nσ(Mn),we have=0,which implies thatni=εn.Therefore,

This forces thatni=εnand

Because[σ(Lm),σ(Mn)]=nσ(Mm+n),we getμ(ε(m+n))=μ(ε(n))forn≠0.Obviously,μ(ε(m))=μ (ε)for allm∈Z.So for allm∈Z,we have

Comparing the coefficient ofon the both sides of

we have

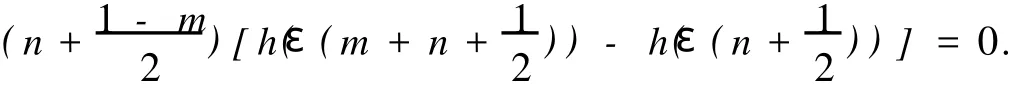
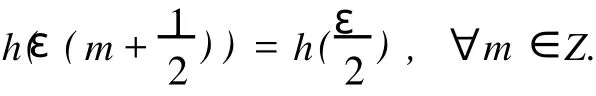
Finally,by the coefficient ofMε(m+n+1)on the both sides of

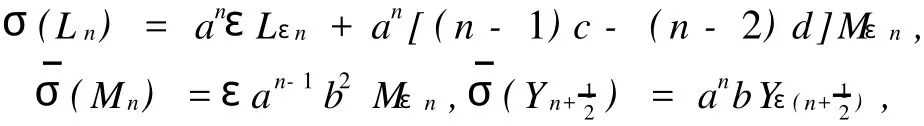
wherea,b∈C＊andc,d∈C.It is easy to check the converse part of the theorem.

Denote byσ(ε,a,b,c,d)the automorphism ofsvsatisfying(2)～(4),thenσ(ε1,a1,b1,c1,d1)= σ(ε2,a2,b2,c2,d2)if and only ifε1=ε2,a1=a2,b1=b2,c1=c2,d1=d2,and

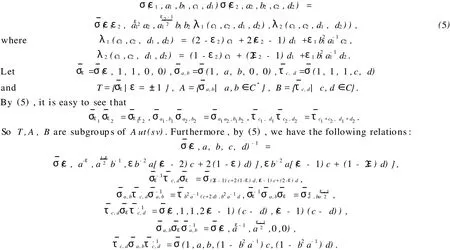
Therefore,Bis a normal subgroup ofA ut(sv)and we have

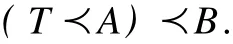
lemma 1.3 A,TandBare all subgroups ofA ut(sv)and

whereT≌Z(yǔ)2={±1},A≌C＊×C＊andB≌C×C.

LetC∞={(ai)i∈Z|ai∈C,all but finitely manyai=0},Gthesubgroupgeneratedby{exp}.ThenC∞is an abelian group.DenoteΓ=G/Γthe quotient group ofG.By(1),we have

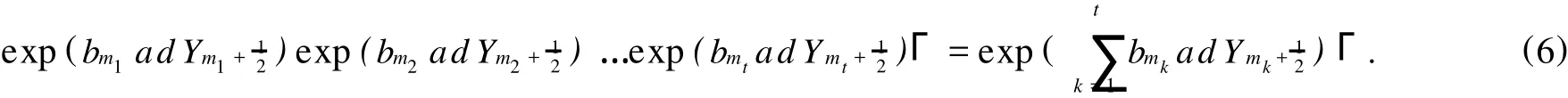
It is easy to deduce that

Proof Define f:Γ→C∞by

whereaki=αkiforki<0,a0=c,andaki+2=αkiforki≥0,the others are zero,ki∈Zandk1≤k2≤…≤ks.Since every element ofJhas the unique formit is easy to check thatfis an isomorphism of group.

Similar to the proof above,it is easy to prove thatvia(6).

[1]HENKEL M.Schr?dinger invariance and strongly anisotropic critical systems[J].J Stat Phys,1994,75:1023.

[2]HAGEN C R.Scale and conformal transformations in Galilean-covariant field theory[J].Phys Rev D,1972,5(2):377～388.

[3]NIEDERER U.The maxiamal kinematical invariance group of the free Schr?dinger equation[J].Helv Phys Acta, 1972,73:802～810.

[4]FEINSILVER P,KOCIK J,SCHOTT R.Representations of the Schr?dinger algebra and Appellsystems[J]. Fortschr Phys,2004,52(4),343～359.

[5]FEINSILVER P,KOCIKJ,SCHOTT R.Berezin quantization of the Schr?dinger algebra,InfiniteDimensional Analysis [J].Quantum Probability and related topics,2003,6(1):57～71.

[6]ROGER C,UNTERBERGER J.The Schr?dinger-Virasoro Lie group and algebra:Representation theory and cohomological study[J].Annales Henri Poincaré,2006(7～8):1477～1529.

[7]GAO S,J IANG C,PEI Y.Structure of the extended Schrodinger-Virasoro Lie algebra[J].Algebra Colloquium,2009, 16(4):549～566.

[8]UNTERBERGER J.On vertex algebra representations of the Schr?dinger-Virasoro Lie algebra[EB/OL].[2007-03-21].arXiv:cond-mat/0703214v2.

[9]GAO S.The structures and representations of Schr?dinger-Virasoro algebras and non-graded Virasoro-like Lie algebras [D].Faculty of Science,Shanghai Jiaotong University,2008:11～14.

MSC 2000:08A35

一類Schr?dinger-Virasoro李代數(shù)的自同構(gòu)群

高壽蘭
(湖州師范學(xué)院理學(xué)院,浙江湖州313000)

為了研究Schr?dinger-Virasoro李代數(shù)sv的結(jié)構(gòu),通過(guò)計(jì)算sv的自同構(gòu)及確定由某些特殊的自同構(gòu)生成的子群之間的關(guān)系,確定了sv的自同構(gòu)群A ut(sv)的結(jié)構(gòu).

Virasoro李代數(shù);Schr?dinger-Virasoro李代數(shù);自同構(gòu)

O152.5

＊Received date:2009-12-21

Biography:GAO Shou-lan,Doctor,Research Interest:Lie algebra.