可變階次的分抗元件的電路實現

張 松

（成都電子機械高等專科學校通信系，四川 成都 610031）

0 引言

分數階微積分運算是整數階微積分運算概念的延伸，分數階運算包括分數階導數和分數階積分、分數階傅里葉變換等，它們是分析和處理許多“非”問題和現象(比如非線性、非因果、非最小相位、非高斯、非平穩、分數布朗運動、混沌等)的有用工具[1]。該問題曾被許多大數學家，如Leibniz、Euler、Liouville等研究過，但是把微積分的階次推廣到分數甚至復數領域，因其計算復雜，過去只是數學家研究的對象。隨著信息科學的迅猛發展,分數微積分的應用也已逐漸滲透到許多工程應用領域, 如各種材資的記憶、力學和電特性描述、粘彈性阻尼器、分形理論等。分數階運算在很多問題的處理過程中所擁有的整數階運算無可比擬的優點正逐漸顯露出來[2]。

數學家們從各自不同的角度入手，給出了分數階微積分不同的定義，如GL(Gainwald—Letnikov)定義、RL(Riernarm—Liouville)定義、Caputo定義等。

從信號處理角度出發，考慮分數演算的頻率域定義為[3]：對于可微的信號f(t)，其傅立葉變換為，即其中v為分數演算的階數（0＜v＜1），可得到分數演算算子在頻域的指數形式為

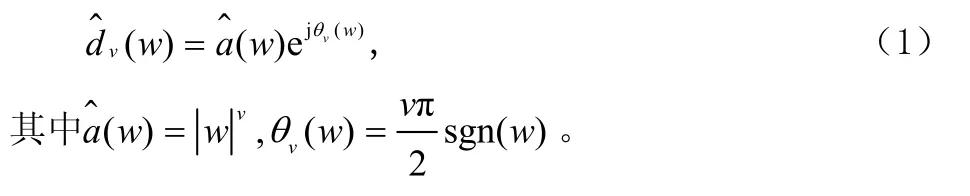
將該定義應用到拉普拉斯變換，即 f( t) ? F( S),則將 Sv定義為拉氏分數演算算子。

拉氏分數演算算子的電路實現將為分數階微積分的工程應用鋪平道路。一些研究者提出了一些實現方法，但這些方法都存在著不同的缺陷。例如：階數限制于1/2階，其它階數不易實現[4]。分抗元件由局部和整體具有高度自相似的分形電路實現，電路元件為無窮多個，不利于集成化。

為此,在參考文獻[5]的基礎上，設計了一款任意階分抗元件，給出其具體設計步驟，并利用該分抗元件可獲得信號的任意分數階微分或積分信號，通過仿真驗證了本設計的正確性。

1 分數階函數（Sν）的逼近

定義每一級雙線性級聯函數如式（3）所示，將其定義為分數階函數的基本模塊函數。

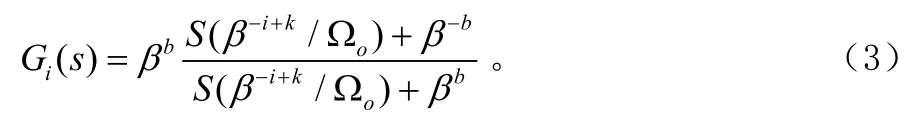
假設待實現的分抗階數為ν=1/3，待逼近的頻率段為（ ΩL,ΩH），其中 ΩL= 2πrad/s,ΩH= 2π ? 106rad/s ，在該頻率段內允許的最大逼近誤差為 εmax= 0 .3 d B ，那么如何實現呢？

⑤令 Ci= β-i+k/Ωo，可得 Ci如下：

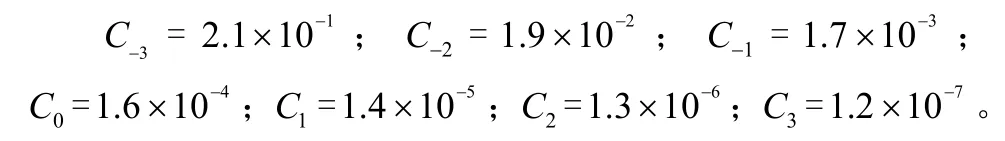
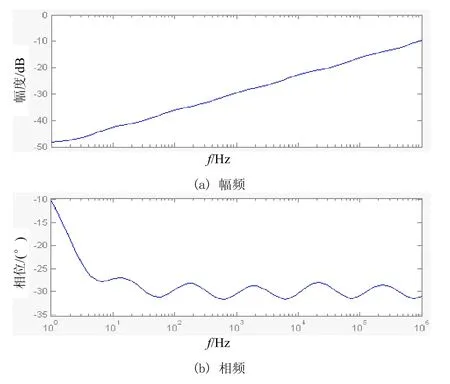
圖1 1/3階分抗元件的幅頻和相頻特性

2 可變階次分抗元件的電路實現

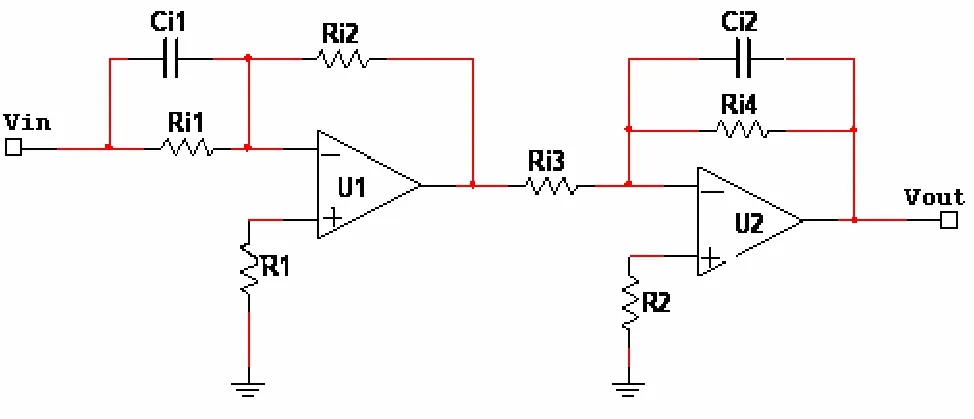
圖2 由比例微分環節和慣性環節組成的基本模塊函數

由比例微分環節和慣性環節的傳遞函數特性，可得電阻、電容參數的設計如式（4）所示：

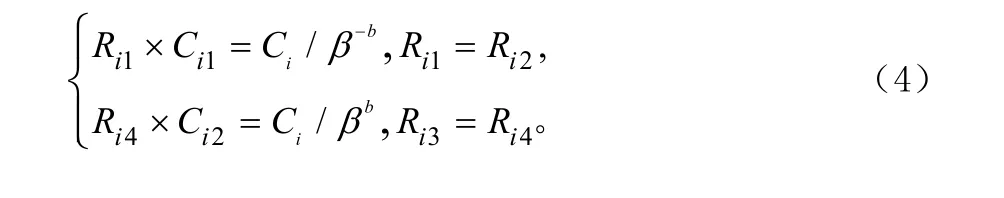
3 電路仿真結果

根據式（2）和式（4）得到其1/3階分抗元件，將如圖2所示的7級電路級聯，其電路如圖3所示[8]。

按照式（4）計算相應的電容電阻值，此處選擇電容在nF或pF范圍內，電阻為1 kΩ到1 MΩ之間，運放選用NE5532，通過Pspice仿真，得到其對應的幅頻和相頻特性如圖4所示。將圖4和圖1比較可知，其電路仿真結果和理論值基本符合。

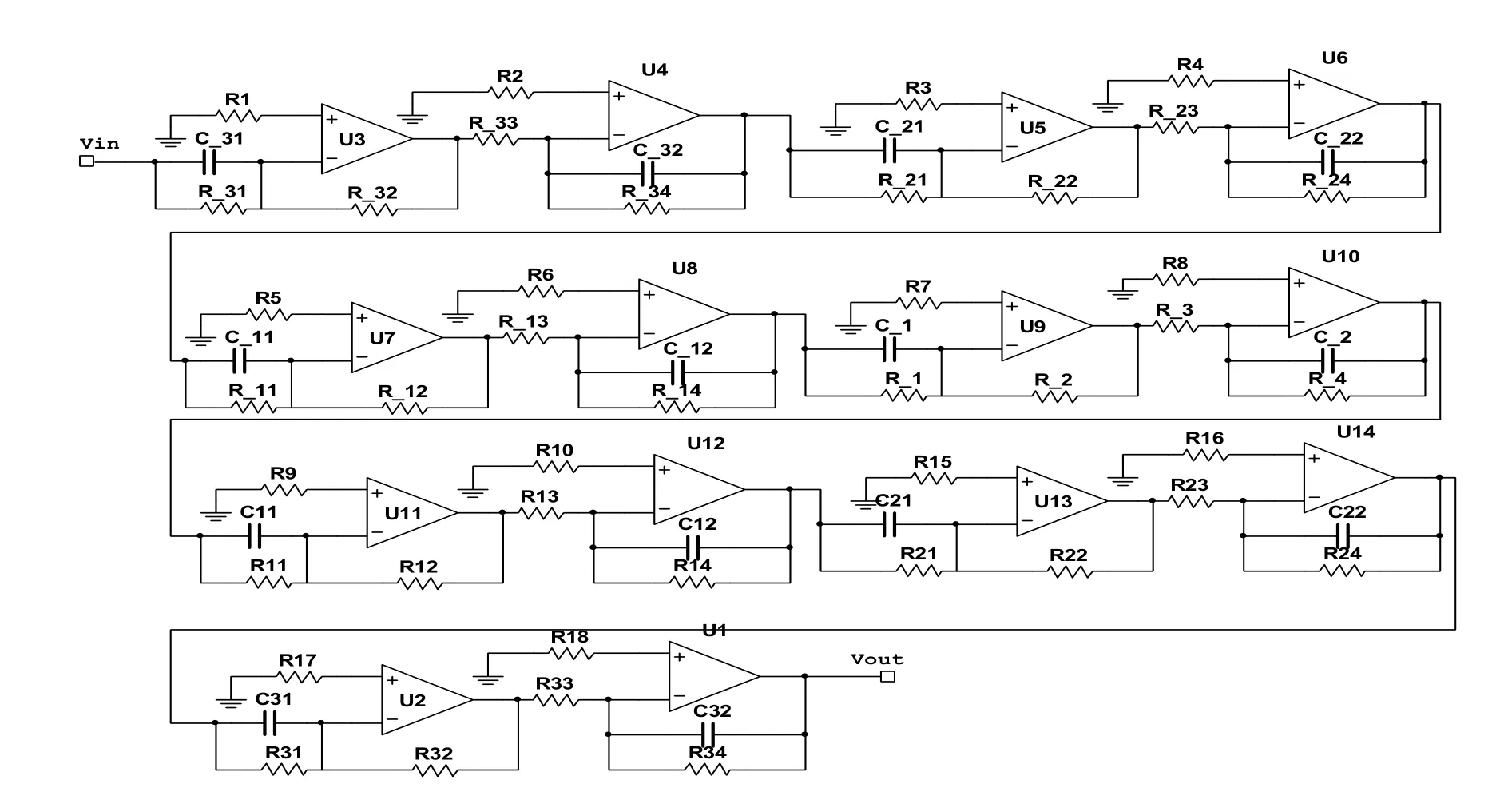
圖3 1/3階分抗元件電路

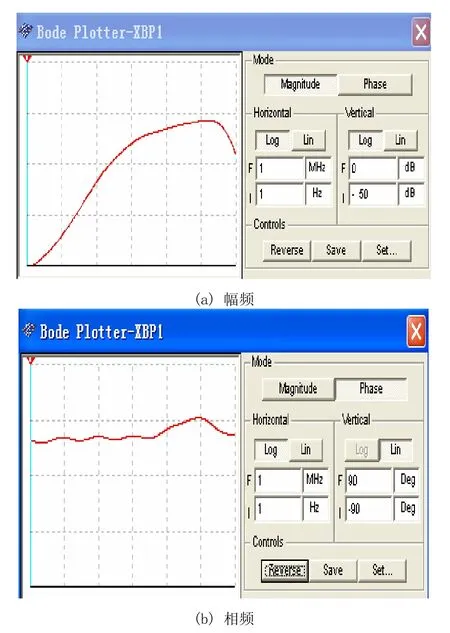
圖4 1/3階分抗元件的幅頻和相頻特性

4 結語

近年來,分數階微積理論成為人們關注的重要課題，如何將分數階運算從理論走向各應用領域，分抗元件的實現是非常重要的環節。利用線性電路完成了可變階次的分抗元件的設計，其設計和實際制作結果逼近理論值，設計電路簡單，容易集成，可根據工程應用需要生產不同類型的分數階芯片，對工程設計具有指導意義。

[1] 袁曉,張紅雨,虞厥邦.分數導數與數字微分器設計[J].電子學報,2004(32)：1658-166.

[2] OLDHAM K B, SPANIER J. The Fractional Calculus[M]. New York and London： Academic Press,1974.

[3] 袁曉,陳向東,李齊良,等.微分算子與子波構造[J].電子學報,2002(30)：769-773.

[4] 廖科,袁曉,蒲亦非,等. 1/2階分數演算的模擬OTA電路實現[J].四川大學學報：工程科學版,2005(37)：150-154.

[5] HISANO T.A Realization of SαTransfer Function[J].Proc.IEICE Fall Conf’.,1992(A-26)：92．

[6] [美] 奧本海姆 A Y,謝弗 R W,巴克 J R.離散時間信號處理[M]．第2版.劉樹棠，黃建國,譯．西安：西安交通大學出版社，2005：171-180.

[7] [美]賽爾吉歐.佛朗哥.基于運算放大器和模擬集成電路的電路設計[M]．第3版.劉樹棠，朱茂林，榮玫,譯．西安：西安交通大學出版社，2004：310-345.

[8] 熊偉,侯傳教,梁青,等．Multisim7電路設計及仿真應用[M].北京：清華大學出版社，2005：247-251.