準雙曲面齒輪切削仿真及齒面誤差分析*

韓佳穎 王太勇 李 清 李敬財

（①天津大學，天津 300072；②天津理工大學，天津 300191）

準雙曲面齒輪切削仿真及齒面誤差分析*

韓佳穎①②王太勇①李 清①李敬財①

（①天津大學，天津 300072；②天津理工大學，天津 300191）

為了縮短準雙曲面齒輪的開發周期和降低成本，采用計算機模擬HFT刀傾法對主動輪進行切削，仿真生成齒輪真實齒面，并以Solidworks為開發平臺進行VBA開發獲得三維齒輪的實體模型。在此基礎上，比較加工齒面與設計理論齒面的差異，對不同加工速度加工的齒輪誤差進行定量計算，說明加工速度對齒面粗糙度的影響。齒面誤差分析結果對生產企業選用什么樣的切削速度進行切削加工提供參考，并有助于TCA、LTCA等研究工作的展開。

準雙曲面齒輪 仿真 齒面誤差

開發一種新車型的后橋螺旋錐齒輪副，其試切開發過程需耗時幾個月，花費數千美元，成本較高，缺乏競爭力［1］。隨著計算機技術的發展，以計算機仿真方法來代替傳統試切過程從根本上解決了這一問題。擬采用計算機輔助制造螺旋錐齒輪，使齒輪的加工、測量過程計算機化，取代傳統的“試切法”，降低開發成本，提高開發效率［2］。合理的數字化實體模型對于計算機輔助螺旋錐齒輪制造來說是必不可少的。當前，基于加工過程的實體建模主要有兩種方式：一種是根據錐齒輪加工原理，選擇并計算齒面上的離散點，進行表面重構［3，4］；另一種是基于加工過程的仿真，再現加工過程，獲得具有真實齒面的齒輪。前者需要求解非線性方程，求解復雜，并且難以反映加工工藝性參數；后者是本文研究采用的基本方法，曾受到計算機速度的限制，難以加工出真實齒面［5］。計算機技術的升級使得這一方法得以實現并能快速建立反映真實加工齒面的三維實體模型，將加工仿真結果與工程實踐相結合，進一步探討加工參數和設計參數對齒面的影響，根據實際需要調整加工參數，切削滿足工程要求的齒輪，實現加工過程優化。

1 螺旋錐齒輪加工制造現狀分析

近幾年，國外已經生產出最新系列的鳳凰II型數控切齒機、磨齒機，加工精度比傳統機床可提高1～2級。雖然數控機床與傳統機床相比優點很多，但是由于其價格高昂，短期內很難在國內普及。國內大多數企業的齒輪加工仍采用機械式螺旋錐齒輪加工機床［6］。

就切削速度而言，國外發展高速干切削，精加工齒面成為趨勢，其切削速度達到300 m/min以上，銑齒精度達到4級、5級。國內銑齒機加工速度一般為20～50 m/min，普遍存在切削速度慢，精度低，效率差的問題。針對國內的這種情況，對機械式螺旋錐齒輪加工機床進行加工仿真，尋求改進設計方案，優化機床的加工調整參數的有效方法。

2 加工仿真實現的方法

2.1 加工過程分析

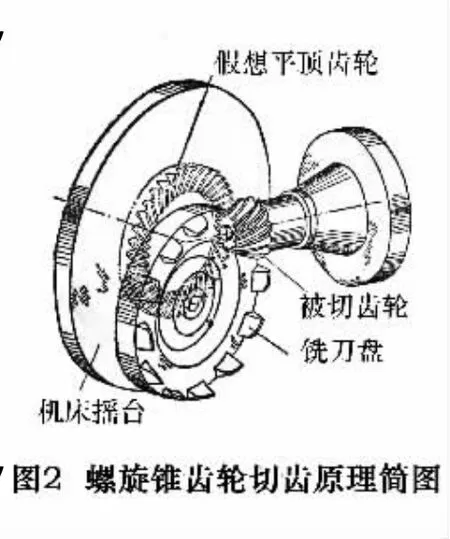
加工仿真是以具有刀傾結構的銑齒過程如NO116銑齒機（圖1）為主要研究對象。銑削加工運動的實質是銑刀盤和工件的相對運動。在切削時，刀傾刀轉機構使刀盤軸線與搖臺軸線傾斜一個角度（刀傾角），而且刀盤隨搖臺擺動形成一個像共軛大輪一樣的假想錐形鏟形齒輪，這個鏟形齒輪按共軛原理與工件按一定傳動比旋轉嚙合。刀盤按一定間隔安裝了刀片，在嚙合過程中刀盤的刀片繞刀軸線旋轉，就像大輪一個牙齒一樣切削工件齒面。某一刀片在銑削刀盤旋轉過刀片間的間隔后，下一刀片開始加工。以此反復斷續加工［7］，每個刀片切去一片金屬，一個切齒循環加工后切出一個齒面，如圖2所示。這個過程的模擬是仿真程序設計的基礎。

2.2 建立簡化模型

基于對加工過程的分析，將刀盤分解成刀片，刀盤和工件的相對運動就簡化為刀片與工件的相對運動。根據實踐工作中使用的調整卡參數確定加工坐標系、加工基本參數、刀盤幾何參數和主動輪幾何參數，由銑齒機刀傾法加工原理建立切削初始模型如圖3所示。在仿真過程中，工件是自轉，其運動連續，所以可簡化為錐臺。刀片的運動為一邊自轉，一邊隨搖臺轉動。由于刀片不是連續切削，所以需要根據切削刀片總數對搖臺轉角進行離散，從而將加工運動離散為切削刀片總數個切削時段。在每一切削時段，切削速度很快，所以每一個刀片的切削掃描體可簡化為一個以刀盤中心軸為軸線的回轉體的一部分，以此模型進行切齒仿真。這里，切削刀片總數是指加工某一牙齒需要參與切削的刀片數，假設切削一個牙的時間為T，刀盤的切削速度為S，刀片數量為N，為了達到較接近于實際加工的齒面，確定切削刀片總數的計算公式為：刀片總數=60T·S·N。如果切削速度S的單位是m/min，刀盤的周長為C，單位為m，切削刀片總數的計算公式變換為60T·（S/C）·N。

2.3 切齒仿真方法［8］

在螺旋錐齒輪的切齒加工過程中，刀片在齒槽中運動并從齒坯上切除部分金屬，而被切除的金屬正是刀片與齒坯之間存在的重疊區域。切齒仿真過程中，在每一個切削時段，通過工件回轉體與刀片回轉體相減的布爾運算模擬切齒加工過程。在所有的切削時段完成以后，齒坯上留下的就是刀具切削刃的包絡面，也就是加工出的工件齒面。

2.4 軟件實現

采用Solidworks為開發平臺，結合VC++語言進行二次開發。在VC++工程文件中建立齒坯、刀具及機床的特征參數，通過 Solidworks命令函數完成生成齒坯、刀具模型的創建，齒坯減刀具的布爾運算等操作。最后，在Solidworks環境中顯示加工過程和加工結果。如圖4所示為主動輪單面法加工仿真結果。該主動輪采取凹面、凸面兩次加工成型，加工后的齒輪具有三維的齒面、齒根及過渡曲面。而且仿真齒面與實際齒面的刀紋是一致的。

3 齒面誤差分析

仿真結果證實，刀片的斷續加工是造成刀紋的原因，也是造成實際齒面與設計理論齒面不一致的主要原因之一。這種斷續加工對齒面精度影響到什么程度，如何影響，需要進行齒面定量計算、測量來分析。通過對仿真齒面的誤差分析可以獲得齒面的誤差大小，為生產企業選用什么樣的切削速度進行切削加工提供參考。

3.1 仿真齒面誤差的分析方法

確定仿真齒面誤差的方法如下：

首先，求解理論方程，獲得理論齒面的坐標值。根據加工過程的理論公式，共軛齒面方程為［9］

其中：角標2表示產形輪；角標1表示主動輪；s表示在刀盤截面上刀尖頂點 M0沿直線刃方向至任一點M的距離（圖5）；q為搖臺擺角， 為刀盤由初始位置轉動角度；n1為M點處法矢量，r1為位置矢量，n12為產形輪與工件的相對速度。該方程為非線性方程，在此采用matlab軟件編程計算，選取恰當的s、q的取值可求出公式中的r1、n1，即可確定理論齒面的坐標值和法矢量。

其次，測量比較理論齒面與仿真齒面的偏差［10］。比較方法如圖6所示，取一個理論坐標值，以點的方式記錄P1，以此點為起點沿n1方向作直線終點為P2，該直線P1P2與齒面曲面相交于一點P3，比較 P1、P3的差值 Δr即為曲面坐標值偏差，記錄所有差值，統計曲面偏差。

3.2 誤差定量分析

外刀切削的凹面為主動輪的工作齒面，選擇的螺旋錐齒輪加工主要參數如表1、表2、表3所示，重點對其進行了仿真和誤差分析。

表1 外刀加工參數

表2 小輪參數

表3 外刀盤參數

仿真后，根據以上方法測量多組對比點統計齒面偏差。統計后發現，齒面上的偏差隨著離散的搖臺角度的變化成呈類似于周期分布。在一個類似周期內，如圖7所示，任取兩個離散的相鄰搖臺角qa、qb間的切削齒面為一測量區間，假設刀片a與刀片b為相鄰兩片刀，刀片a退出切削的搖臺角為qa，刀片b進入切削的搖臺角為qb。在此區間內沿兩個方向選取對比點與設計理論值相比較：

當s取值一定時，q取多組數值，其測量點沿齒面齒長方向分布（如圖8所示）。搖臺旋轉到qa、qb時偏差幾乎為0；越靠近qa或qb，偏差越小，搖臺旋轉到qa、qa中間時偏差最大，即刀紋Ca、Cb附近處偏差最大。

當q取值一定時，s取多組數值，其測量點沿刀紋方向分布。沿刀紋方向，齒根處偏差小，齒頂處偏差大。

對于整個凹面，切削仿真生成的凹面刀紋齒頂疏齒根密，小端刀紋密，大端刀紋疏。切削模型齒面刀紋稀疏處最大偏差較大，而且沿刀紋附近偏差較大。但是大端和小端偏差相差不明顯。與凹面有所不同的是，凸面大端和小端偏差差別相當明顯。比如，切削刀片總數為120刀時，小端偏差＜2 μm，大端偏差可達30 ～40 μm。

以上對仿真齒面的統計與三坐標測量機測量的真實齒面以及經驗數據是一致的，由此證明本文所采用的方法是正確的。

3.3 實例對比

刀片切削數量是齒面偏差的成因之一，也是加工效率的重要影響要素。采用同一機床，刀片數多，刀紋密，齒面偏差小，表面粗糙度值小，但是花費時間多，效率差；刀片數少，刀紋疏，齒面偏差大，到一定程度就會影響到齒面精度。由此采用仿真及誤差分析的方法對切削速度的調整，使得在不影響齒面精度的前提下，選用最經濟的轉速成為可能。針對以上加工參數，選取不同加工刀片數，切削齒面的凹面偏差對比如表4。格里森公司根據實驗確認：當兩曲面之間的距離Δδ≤6.35 μm時，用紅丹粉可以檢查出齒面的接觸印跡［9］。所以，對于本文所提供的實例，選取刀片總數為100～120這個區間的刀片總數是比較合理的，既不影響切削精度也不影響切削效率。

表4 凹面偏差對比

選用不同加工機床，以上述加工參數來加工齒輪，切削刀數量對比如下：

（1）以國內機床進行加工，選用12英寸刀盤，刀片數量20，切削速度50～60 m/min，單面切削每個齒每面切削時間40～60 s。經計算，單面切削一個齒切削的刀片數量約為70～125片，參照表4，齒面偏差可以接受。

（2）鳳凰高速干切削機床，根據調整卡，刀盤轉速113 r/min，刀片數量10，單面切削每個齒每面切削時間9.5 s。切削的刀片數量約為187片。

數據對比證實，如果選取較長的切削時間，國內所采用的切削速度不會影響齒面精度，可以獲得與設計一致的接觸區。只是相比于鳳凰機床，國內機床切削速度慢，效率低，刀片間隔大會產生明顯的刀紋，使得表面粗糙度值增大，增加了研齒的難度。根據以上分析，結合工程實踐提出以下改進建議：

（1）根據刀片總數來判斷切削精度，選取合理的切削時間和切削速度。國產機床精度差，可提高刀盤轉速，降低搖臺轉速，以增加切削刀片的數量。該方法的弊端為增加了切削時間，降低了工作效率。鳳凰機床可適當縮短切削時間，進一步提高工作效率。

（2）對于刀片總數過少的加工，達不到切削精度，可通過后一道工序如研齒、磨齒進行改進。

（3）推陳出新，發展高速干切削。加工相同精度的齒輪，高速干切削可以將加工效率提高2～5倍，而切削刀片總數多使高速干切削可以達到很光滑的切削表面，齒面粗糙度和精度可達到很高水平。相對于濕切削，高速干切削不但能夠提高生產效率，而且大大減少了研齒的難度，值得推廣。

4 結語

基于加工過程的螺旋錐齒輪仿真的實現以及齒面偏差的定量分析為以下工作的開展打下了良好的基礎：

（1）得到能反映真實加工過程的齒面，通過參數調節可方便對螺旋錐齒輪的變性法、刀傾法的加工過程進行仿真，也可實現各種加工修正模型的構建。以此為基礎可進一步開發TCA程序，實現齒面接觸區修正，用于指導生產。

（2）定量分析了仿真齒面與設計齒面的偏差，通過增加切削刀片數，在計算機允許范圍內，可以使仿真齒面最大限度地接近于設計齒面，有助于設計結果的檢驗，實現設計參數的優化。

（3）快速獲得螺旋錐齒輪三維模型，并能使齒面、過渡曲面及齒根曲面通過一次建模同時得到，有助于有限元分析的開展，為真實齒面的LTCA研究創造條件［11，12］。

1 謝華錕譯.螺旋錐齒輪的開發：用計算機技術淘汰試切法［J］.工具展望，2006（4）：14 ～16

2 王沉培，周云飛等.計算機輔助設計在準雙曲面齒輪數控化加工中的應用［J］.計算機輔助設計與圖形學學報，2002，14（4）：320 ～323，328

3 王延忠，阮德林，趙興福等.螺旋錐齒輪離散齒面數字仿真加工方法研究［J］.機床與液壓，2007，35（2）：24 ～26

4 李敬財，王太勇，何改云等.基于加工方法和嚙合理論的螺旋錐齒輪精確實體造型［J］.吉林工大學報，2008，38（6）：1315 ～1319

5 于水琴，曾韜.數控螺旋錐齒輪磨齒機加工仿真系統的研究［J］.機械制造，2008，46（3）：5 ～7

6 李兆文，王勇，陳正洪.螺旋錐齒輪技術的研究現狀［J］.工具技術，2007，41（4）

7 北京齒輪廠.螺旋錐齒輪［M］.北京：科學出版社，1974.

8 熊越東，王太勇，張威.螺旋錐齒輪數控銑齒加工過程幾何仿真研究［J］.機床與液壓，2005（6）：1 ～3，88

9 曾濤.螺旋錐齒輪設計與加工［M］.哈爾濱：哈爾濱工業大學出版社，1989.

10 陳書涵，嚴宏志，明興祖等.螺旋錐齒輪誤差齒面及差曲面的建立與分析［J］.中國機械工程，2008，19（18）：2156 ～2161

11 Faydor L.Litvin，Alfonso Fuentes，Kenichi Hayasaka.Design，manufacture，stress analysis，and experimental tests of low － noise high endurance spiral bevel gears［J］.Mechanism and Machine Theory.2006，4（1）：83－l18

12 Qi Fan.Computerized Modeling and Simulation of Spiral Bevel and Hypoid Gears Manufactured by Gleason Face Hobbing Proces［sJ］.Journal of Mechanical Design，2006，128（6）：1315 －1327

如果您想發表對本文的看法，請將文章編號填入讀者意見調查表中的相應位置。

Computer Cutting Simulation and Deviation Analysis of Tooth Surface for Hgpoid Gears

HAN Jiaying①②，WANG Taiyong①，LI Qing①，LI Jingcai①
（ Tianjin University，Tianjin 300072，CHN；②Tianjin University of Technology，Tianjin 300191，CHN）

Computer cutting process simulation of hgpoid gears（ HFT ）is applied for reducing the developing cycle and cost of hgpoid gears.Based on Solidworks development platform and the VBA programming language embedded in Solidworks，the three －dimensional driven gear model is created with true tooth surface.By comparing theoretical tooth surface with the cutted one，compute the deviation of tooth surface to achieve the surface roughness of gears in different cutting speeds.The result provides the reference for factories in choosing the cutting speed and supports the research on TCA，LTCA，etc.

Hypoid Gears；Computer Simulation；Deviation of Tooth Surface

*國家863項目（2006AA04Z146），（2007AA042005）和高等學校博士點專項科研基金（20060056016），天津市科技支撐計劃重點項目（08ZCKFGX00900），天津市科技計劃項目（08ZCKGX02300），禹州市鈞瓷研究所項目（G208591）

韓佳穎，女，1979年生，博士研究生，從事齒輪數字化制造及機械自動化研究。

（編輯 譚弘穎） （

2009―06―09）

10136