剪切流中立管的渦激振動響應預報
高 云, 曹 靜, 宗 智, 周 力
(1.大連理工大學工業裝備與結構國家重點實驗室,大連 116024;2.大連理工大學運載工程與力學學部,大連 116024;3.中國海洋石油總公司研究中心,北京 100027)
剪切流中立管的渦激振動響應預報
高 云1,2, 曹 靜3, 宗 智1,2, 周 力1
(1.大連理工大學工業裝備與結構國家重點實驗室,大連 116024;2.大連理工大學運載工程與力學學部,大連 116024;3.中國海洋石油總公司研究中心,北京 100027)
針對鋼懸鏈式深海立管的特點,采用簡化后的振動模型,結合圓柱體的受迫振蕩實驗數據,建立了深海立管在剪切流來流中的渦激振動響應分析模型。被激起的各階模態的響應位移可通過平衡立管升力的輸入能量和阻尼的耗散能量計算得到。計算結果與渦激振動專用分析軟件計算結果進行了對比,吻合良好。
深海立管;鋼懸鏈式立管;渦激振動;升力;阻尼
Abstract:According to the characteristic of the deep-water steel catenary riser,a model is presented to predict the response of vortex-induced vibration(VIV)in sheared flow based on the dates from tests with cylinders.The displacement of each excited mode is determined by a balance between the energy fed into the riser by lift force and the energy dissipated by damping.The analytical results match the results calculated by VIV professional software well.
Key words:deep-water riser;steel catenary riser;vortex-induced vibration;lift force;damping
0 引言
海洋立管在進行石油和天然氣開采中起著重要作用。當海流流過立管時,由于結構的存在,產生流動分離現象,進而發生旋渦脫落和周期性的尾流。周期性的旋渦脫落會在立管上產生與流向垂直的周期性的力,從而使立管在橫流方向上發生振動,通常稱之為渦激振動。
當立管的工作環境為均勻流時,對立管進行渦激振動響應預報比較容易。但當來流不是均勻流,而是更切合實際海洋工作環境中的剪切流時,渦激振動機理要比均勻流復雜得多。在剪切流中,立管的多個模態參加了激勵振動。
1 數學模型
1.1 立管振動的簡化模型
本文所分析的立管為鋼懸鏈式立管,因鋼懸鏈式立管通常是處在深水的工作環境中,立管的長度和直徑比值很大,所以需要慮及立管的柔性特征。鑒于本文所分析的立管的L/D比值大于200,由自由懸掛管線的規范[1]提供的關于管線L/D變化時管線特性可知:立管在實際工作過程中所表現出來的力學性質是索的特性,而不是梁的特性。所以,在分析過程中應把鋼質懸鏈式立管作為張力索來處理,而不是作為通常的彈性梁來處理。
第 n階固有頻率ωn(單位:弧度/s)可表示為[2]

式中:L為立管長度;n為模態階次;s為沿立管軸線方向的坐標;T(s)為坐標s處的有效張力;mt(s)為單位長度的總質量(包括立管凈質量、內部流體質量以及附加質量)。
立管第 n階模態振型可表示為

立管第 n階模態曲率可表示為

式中 x為立管的軸向坐標(坐標原點取在立管下端張力最小處)。
1.2 激勵模態識別
(1)能量激勵區域的計算
當計算第 r階模態的能量輸入區域時,需要先判定第 r階模態的約化速度范圍,約化速度可表示為[3]

式中:V(x)表示x處的來流速度;D(x)表示x處的立管直徑;VR(x)表示第r階模態x處的約化速度;fr表示立管第r階固有頻率(單位:Hz)。
根據給定的一個約化速度雙帶寬b的值,則可得到:VL=VP-0.5bVP,VH=VP+0.5bVP(VP=S-1t,St為斯脫哈兒數)。當第r階模態x處的約化速度處于第r階模態約化速度帶寬內,即VL≤VR≤VH,則認為流體將激勵立管并導致立管對該模態的響應。
(2)潛在激勵模態識別
根據斯脫哈兒頻率與流剖面計算旋渦泄放頻率范圍,旋渦最小與最大泄放頻率可根據下式計算:

式中:Umin和Umax分別為流剖面的最小與最大速度。若某階固有頻率在最小和最大泄放頻率范圍內,則認為該模態被激勵。
處在泄放頻率帶以外的邊界模態根據以下原則進行判別:
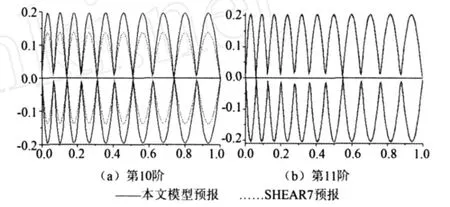
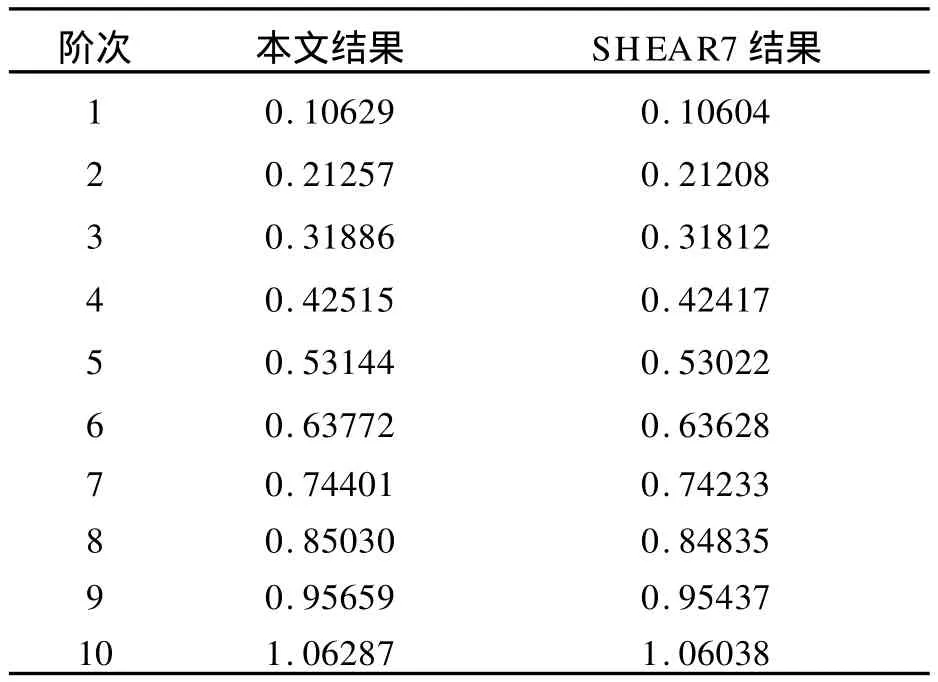
①高邊界模態識別,如果 (fj+fj+1)/2 ②低邊界模態識別,如果 fi (3)主要激勵模態識別 在以上判斷的潛在激勵模態中,可進一步對主要激勵模態進行識別。先按下式對各階激勵模態的振動能量進行初步的估算: 找到振動能量最大的模態,以其能量值作為一個基準,將其余各階模態的振動能量與之相除,得到一個能量比。用戶可選擇一個閥值,低于該閥值模態將被篩除。若大于閥值的模態數只有一個,則進行單模態鎖定響應計算。否則進行多模態響應計算。 1.3 渦激振動響應幅值 把立管簡化為兩端鉸支的索模型,坐標原點取在立管下端張力最小處,建立立管的振動方程: 式中:ρf為海水密度;D(x)為立管水動力作用直徑;V(x)為x處的水流速度;ωr為旋渦脫落頻率;CL(x;ωr)為ωr的旋渦脫落頻率下x處的升力系數。 式中:Yr(x)為立管的歸一化振型;qr(t)為立管的模態坐標。qr(t)可表示為 式中Ar為第r階模態的振幅。將(10)式代入控制方程,得到: P(x,t)為升力分布,可表示為 由該平衡表達式,可達到預測模態振幅的公式,可表示為 1.4 流體力模型 (1)升力模型 對于某階特定的模態來說,升力系數 CL和無量綱振幅比Ar/D的關系可根據實驗數據的四個值擬合得到兩條分段拋物線。四個值分別為:當 CL為0時,A/D的取值;當 CL得到最大值時,A/D的取值;CL的最大值的大小;當 A/D為0時,CL的取值。 (2)流體阻尼模型 本文中,采用Venugopal[5]提出的非線性阻尼模型來進行計算。在文獻[5]中,綜合了大量實驗數據并為局部流體阻尼常數推薦了下面的經驗模型rh(x)。這個模型依賴于局部約化速度并且當約化速度大小不同時,表達式是不相同的,阻尼模型由兩個不同的區域組成。 低約化速度阻尼模型:Rh(x)=Rsw+CrlρDV(x)(18) 式中:Rsw為靜水的分布;Crl為經驗系數,當前可取0.18。靜水的分布可表示為 式中 Crh為另外一個經驗系數,通常取為0.2。 2.1 計算模型 本文計算的立管模型參數如表1所示。 2.2 模態分析 本文模型計算得到前10階固有頻率,和SHEAR7計算結果對比如表2所示。 表1 立管基本參數 表2 固有頻率(單位:弧度/s) 2.3 激勵模態識別 (1)潛在激勵模態識別 根據1.2中判斷方法,得到被激起的潛在模態階數為第3~12階。 (2)能量激勵區域的計算 將立管沿長度方向均勻分成200個單元,坐標原點位于下端點處。則立管總共為201個節點,從下至上的節點號遞增,從第1號節點依次增加到第201號節點。表3給出了本文模型計算和SHEAR7計算的潛在激勵模態下的能量激勵區域(節點范圍)。 表3 能量激勵區域 (3)主要激勵模態識別 選取0.5為閥值,根據能量比得到激起的模態數為第10階和第11階。 2.4 響應幅值的計算 根據公式(17)進行計算,計算過程需進行多次迭代。先給 Ar/D賦予一個初值,記做:(Ar/D)0。根據圖1中的曲線和初值計算得到一個升力系數。將此升力系數帶回到式(17)中,得到新的 Ar/D,記做:(Ar/D)1。依此類推,迭代了k次后的Ar/D記做(Ar/D)k,k+1次后的Ar/D記做(Ar/D)k+1。預先給定一個相對誤差的收斂準則,設為V(Ar/D)。當滿足式(22)時,則認為迭代收斂,即終止迭代計算。 第10階橫向響應幅值的包絡線對比如圖1(a)所示,第11階橫向包絡線對比如圖1(b)所示。 本文針對鋼懸鏈式立管的特點,建立了簡化后的張力索模型,并結合圓柱體的受迫振蕩實驗數據,對深海剪切流中的立管渦激振動進行了響應預報。由以上的分析計算可得到如下結論: (1)由渦激振動響應幅值的表達式以及升力系數曲線可以看出:升力系數影響渦激振動響應幅值,響應幅值同時又影響升力系數。這恰恰反映了渦激振動是一個流固耦合現象,只有通過迭代計算,才可以得到比較準確的解。 (2)無論是模態振型圖還是模態曲率圖,當坐標越靠近頂端時,相鄰兩個峰或谷所對應的立管長度越大。這反映了立管的變張力特性。 (3)當來流為剪切流時,立管則有多個模態參加振動。可先根據流剖面的速度、斯脫哈兒數、立管直徑以及立管的固有頻率,辨別出潛在激勵模態。然后,需要定義一個能量比的閥值,再在潛在激勵模態中分辨出哪些模態為主要激勵模態。主要激勵模態外的其他模態則被認為不參加振動。 [1] DNV.DNV-RP-F105.Free Spanning Pipelines[S].Norway:GCS AS,2002. [2] Vandiver J K,Li L.SHEAR7 V4.4 PROGRAM THEORETICAL MANUAL[M].Department of Ocean Engineering Massachusetts Institute of Technology,Massachusetts Institute of Technology,Copyright 2005. [3] Vandiver J K,Li L.Prediction of Beams or Cables with Slowly Varying Tension in Sheared or Uniform Flow[M].Department of Ocean Engineering Massachusetts Institute of Technology,Massachusetts Institute of Technology,Copyright 2005. [4] Vandiver J K,Chung T Y.Predicted and measured response of flexible cylinders in sheared flow[C].Proceedings of the ASME Winter Meetings,1988. [5] Venugopal M.Damping and response prediction of a flexible cylinder in a current[M].Department of Ocean Engineering Massachusetts Institute of Technology,1996. Predicted Response of Riser in Sheared Flow GAO Yun1,2, CAO Jing3, ZONG Zhi1,2, ZHOU Li1 圖1 橫向響應幅值包絡線對比 P756.2 A 1001-4500(2010)03-0021-05 2009-12-08 創新研究群體科學基金(基金編號:50921001) 高 云(1985-),男,博士生,從事海洋工程研究。

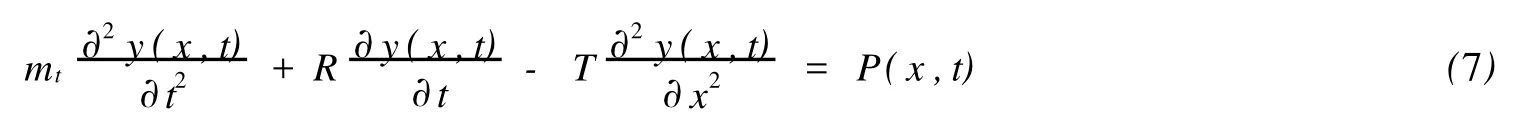
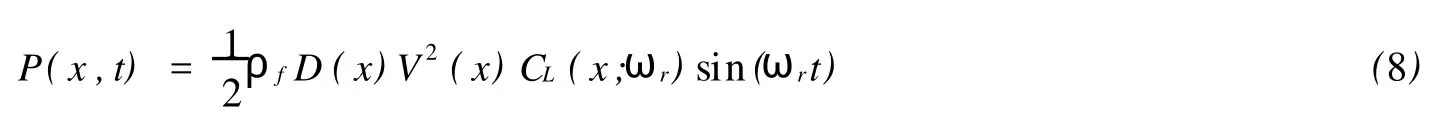



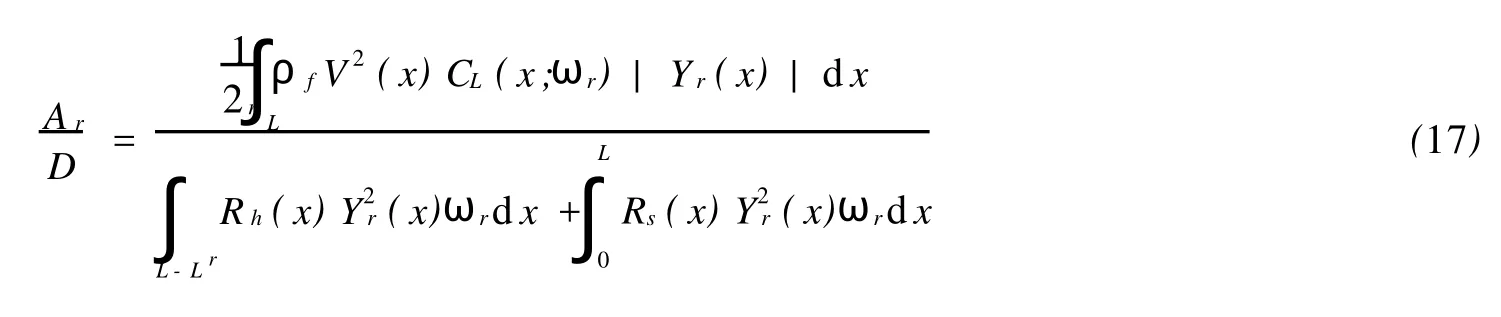

2 算例分析



3 結論
(1.Industry equipment and structure state key library,DaLian University of Technology,Dalian 116024,China;2.Faculty of vehicle engineering and mechanics,DaLian University of T echnology,Dalian 116024,China;3.Technology research department,China National Offshore Oil Corporation,Beijing 100027,China)