182Os核 yrast帶結構SU(3)→U(5)→SU(3)形狀相變的有序性研究*

童紅張春梅石筑一?汪紅倪紹勇

1)(貴州民族學院物理系，貴陽550025)2)(北方民族大學基礎部，銀川750021)

(2009年3月9日收到;2009年8月6日收到修改稿)

182Os核 yrast帶結構SU(3)→U(5)→SU(3)形狀相變的有序性研究*

童紅1)張春梅2)石筑一1)?汪紅1)倪紹勇1)

1)(貴州民族學院物理系，貴陽550025)
2)(北方民族大學基礎部，銀川750021)

(2009年3月9日收到;2009年8月6日收到修改稿)

對于發生在同一個原子核中的轉動誘導發生基準態結構的量子相變，可以理解為一種從高有序激發模式向著低有序激發模式的演化:被布居到高角動量態的高有序激發核，以E2躍遷的方式先行退耦到yrast帶，再退耦到共存區(或臨界點)時釋放了有序的結構能，誘發價核子對耦合強度改變，重新組合出低有序的激發模式基準態，實現了基準態結構的過渡.對核量子相變的這種描述，與朗道經典熱相變理論之間有了某些相似的術語和物理內涵.本文把這種理解推廣到了相繼的二次相變中.以182Os核為例作了說明，并展示了核結合能對核結構的極端敏感性.

量子相變，基態結構演化，微觀sdIBM-max方案，182Os核

PACC:2110R，2160E，2320L

1. 引言

在核物理學中，人們異常關注“量子相變”(QPT)現象，這是一種發生在零溫度上的結構改變，并受到量子漲落驅動和非熱力學參數控制的現象，而成為哈密頓量中耦合常數的函數［1—7］.熟知，核能譜的典型特征取決于核子對的形成或者潰散，這又重新喚起了人們對相互作用玻色子模型(IBM)研究及其應用的興趣.按照習慣，描述一群原子核隨玻色子數改變所引起的從球形到變形的相變，稱為“基態量子相變”(GSQPT，最新綜述見文獻［4］)［1—12］;而描述單個原子核隨角動量改變所導致的從集體振動激發模式到集體轉動激發模式的相變，叫做“轉動驅動形狀相變”(RDSPT，綜述見文獻［5，8］)［5，8，13—19］，它們都是所謂的核形狀相變(NSPT)的研究內容.長期的研究顯示:研究NSPT對稱性方面的方便框架是IBM;把GSQPT和RDSPT統稱為基態能量相變(ground-state energy phase transitions，GSEPT)［14］，凸現了基準態結構改變及其相應的能量改變是NSPT的本源.它旨在專門研究在低能、低角動量態上原子核對稱性的改變現象和揭示其規律.顯然，對于后者的深刻理解是全面認識前者的線索.就目前而言，屬前者范疇內的SU(3)→O(6)，U(5)→O(6)和U(5)→SU(3)的GSQPT描述較為成功，而對后者范疇內的RDSPT才剛剛引起重視［5，8，13—19］.

盡管，對Hf—Hg同位素是否存在有兩級SU(3)→O(6)→SU(3)的GSQPT爭論比較大［4，12］.但是，182Os具有兩級SU(3)→U(5)→SU(3)的RDSPT得到來自實驗數據整理結果的支持［4］.不管怎樣，理解相變臨界點上原子核中有限中子-質子組分怎樣引起結構調整仍是一個重要問題.這在唯象理論中還不是完全清楚;若能從有限核子組合機理去闡明和理解這些現象將是很有意義的［1，6，9］.其實，從微觀角度看，它們只是原子核中的核子耦合、配對、拆對、拆對-順排、拆對-重新耦合以及基準態重組各種功能的宏觀表現而已［16—26］.

在描述102Ru［17］，128Ce［18］和76Sr［19］核的RDSPT中，曾經設想過:在高激發核的退耦進入對稱性共存區時，高激發-高有序的基準態釋放結構能，導致價核子對耦合強弱的變化，“重組”出新的低激發-低有序的基準態，完成高-低有序基準態之間的過渡，實現了RDSPT.這種設想是可以推廣去描述同一原子核相繼發生兩次RDSPT的結構演化.本文試圖以182Os核為例，深入研究這類相繼相變，并給出對這種微觀機理的進一步理解.

2. 理論方案

在原子核的微觀理論中，價核子體系的哈密頓量一般地可以表達為［20，21］

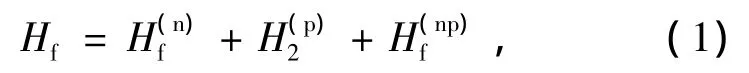
其中各項簡寫為

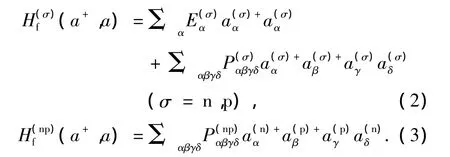
當對具體核進行計算時，核子-核子有效相互作用取為對力、四級對力和四級-四級力.

利用Dyson玻色子展開和MJS代換，將核體系費米子描述的Hf(a+，a)轉變為理想玻色子描述的HB(A+，A).為了確保A-玻色子的集體性(有序)，引入一組Q-玻色子

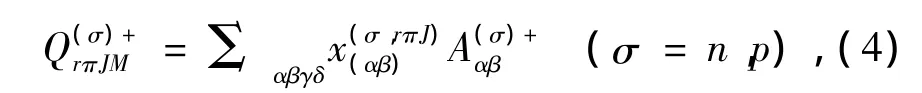
借助本征方程

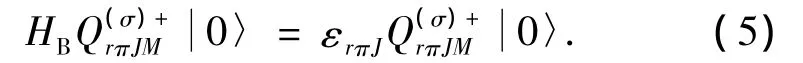
可以確定(4)式中的玻色子結構常數x((σαβ，)rπJ).在最低階近似下，把唯象IBM中的s，d玻色子定義為

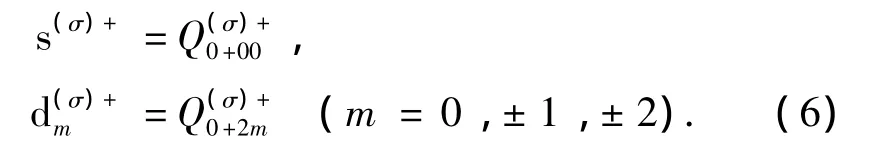
再對玻色子哈密頓量H(σ)B作s，d截斷，便得到

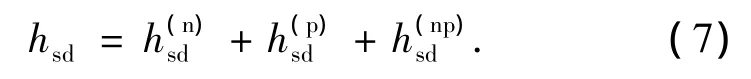
這樣就構造出了微觀sdIBM-2方案中最普遍的哈密頓量.其中各項系數均可表為同種價核子間的對力、四極對力、四極-四極力、中子-質子的四極-四極力的相互作用強度參數g(σ)0，G(σ)2，K(σ)(σ=n，p)，K(np)，和能級量子數α的解析形式，這可在文獻［20，21］中找到;在相應的玻色空間對角化(7)，將得到核體系的能譜.

從幾何學和物理學的角度看，上述操作可以理解為:在無相互作用的費米子空間中，對費米體系實施玻色子化時，能級α，β上的核子，除α=β外，將以概率交叉配對出理想玻色子;在集體化的過程中，理想玻色子的線性組合又將玻色子能級交叉和扭曲了，構造出一個結合能不同、具有某種對稱性的激發元及其基準態，即成為具有某種激發模式的、準-同核異能的基準態(quasi-isomeric basic states)，核子的相應狀態被賦予了不同的有序性(用結合能量度)和某種對稱性.這樣，玻色子獲得了總結合能:核子對的束縛能(即配對能是單粒子能量值)和核子對之間的相干能(即成序能|E(σ)st|)，它可視為對核有序結構的度量;且

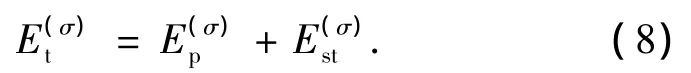
具有同一對稱性的激發事件發生在同一種子結構中(躍遷);而不同對稱性結構的基準態之間，或玻色子數不同的基準態之間，也會引發基準態的過渡事件，前者為RDSPT，后者為GSQPT.凸現了把這種基準態的變更定名為GSEPT的精妙.

我們用于描述核體系出現基準態結構改變的哈密頓量，是微觀IBM方案中s，d價核子對的、最普遍形式的哈密頓量，而不是一般文獻中經常選用的潛在對稱性哈密頓量的線性組合(簡稱為Ising型)［4，5］.方案本身不具有原始對稱性，客觀;價核子對具有物理結構，不是簡單的、幾何的剛性粒子，能研究玻色子拆對與基準態重組的細節;還能計算出核子配對能與核子對有序結構能，能揭示基準態的有序度，是其他方案所不及的;它既有區分中子-質子的精確方案，又有不區分中子-質子的最大同位旋近似的sdIBM-max方案(本文將使用的)，便于按需選擇.但是，方案的缺陷是它不能準確指認能譜的精確對稱性，需另行分析.

3. 計算結果和討論

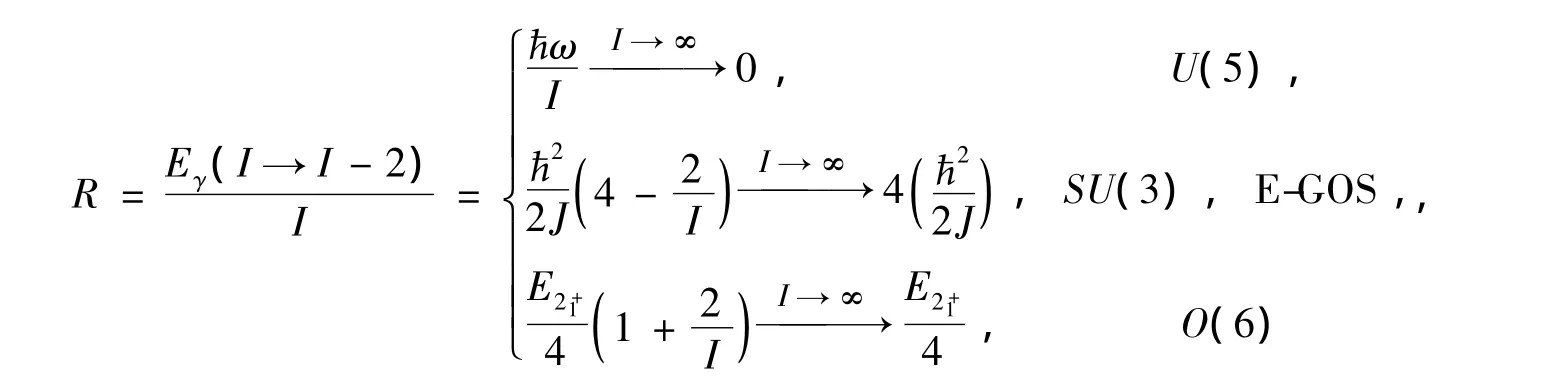
借助能夠證明沿著yrast線發生激發模式改變的一個很敏感的指證判據R［5］，及其對182Os的實驗E-GOS曲線構成的理論譜分析［24］(見圖1)，清楚地看到182Os的實驗yrast態的E-GOS曲線被很好地分為21+—41+態、81+—181+態和181+—341+態三段曲線，它們分別是理想SU(3)轉子模式、理想U(5)振子模式和另一個理想SU(3)轉子模式能級的E-GOS曲線;其間有兩次RDSPT的相變共存態61+和181+態.對于361+，381+態，傳統上指認它們是兩粒子態，而文獻［28］卻推測它們是由高-K振動態變更過來的yrast態，本文將不予研究(圖1中也沒有畫出).

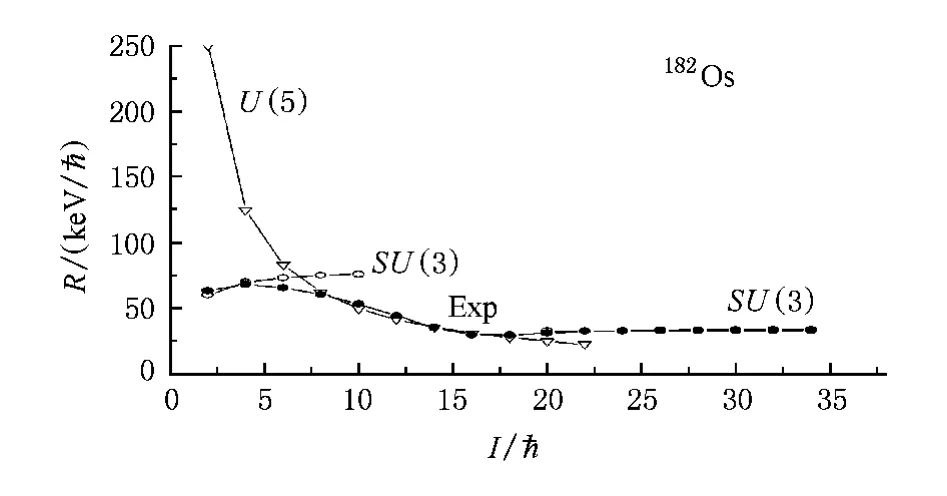
圖1182Os核實驗能譜［27］的E-GOS分析

對于這里發生的SU(3)→U(5)→SU(3)的兩次RDSPT，應該怎樣理解?最初，文獻［28，29］在解釋U(5)→SU(3)→U(5)的實驗事實時認為:在高自旋態上，能量有利于振動態.從微觀IBM角度看，由于核中有限量子的零點運動，狀態的漲落會產生真實的形狀躍變.事實上，對于SU(3)→U(5)→SU (3)相變，原子核的基準態中本來就存在有球形和弱變形的競爭，因為旋轉性不夠和價玻色子較多，原始分布的不均勻性造成了能量上有利于弱的軸對稱性旋轉形狀［SU(3)］，這時集體性不強、有序度不高.以后，隨著旋轉的加強，玻色子分布逐漸趨于均勻，出現球對稱性［U(5)］的概率逐漸增加，發生了第一次RDSPT.當旋轉更強時，對剛性較好的核，漲落促成一個以上的玻色子脫離集體芯核，并繞其旋轉，呈現所謂的“玻色子-核芯轉子”模式，但它仍舊屬集體激發;對剛性強度不夠的核，在出現變形并穩定下來時，便形成了新的基準態，又一次發生了RDSPT.最后，更高速的旋轉迫使旋轉著的玻色子發生拆對-順排，成為“核子-核芯轉子”模型，單粒子激發及回彎現象也就發生了.

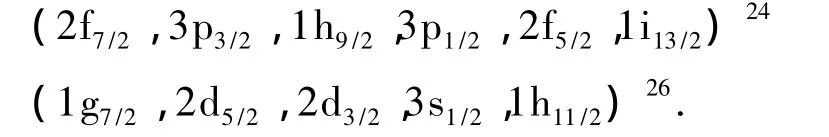
表1 實驗單粒子能量值(MeV)

表2 核子-核子等效相互作用參數(MeV)

表3顯示，用三組參數分別再現的各段yrast線與實驗測量值相符合得很好［24］.低能激發模式很好地再現了2+1和4+1態;中能激發模式對6+1—10+1態的再現值稍稍大一點，但12+1—18+1態的計算值與實驗值卻又符合得很好;最后，高能激發模式很好地再現了18+1—34+1態的能譜，整體再現得頗為滿意.計算還揭示182Os核的相變共存區就是相變臨界點，6+1和18+1態，與實驗結果完全一致.

表3182Os核yrast譜的理論計算值與實驗值［27］的比較(MeV)

表4182Os核的某些能量值(MeV)

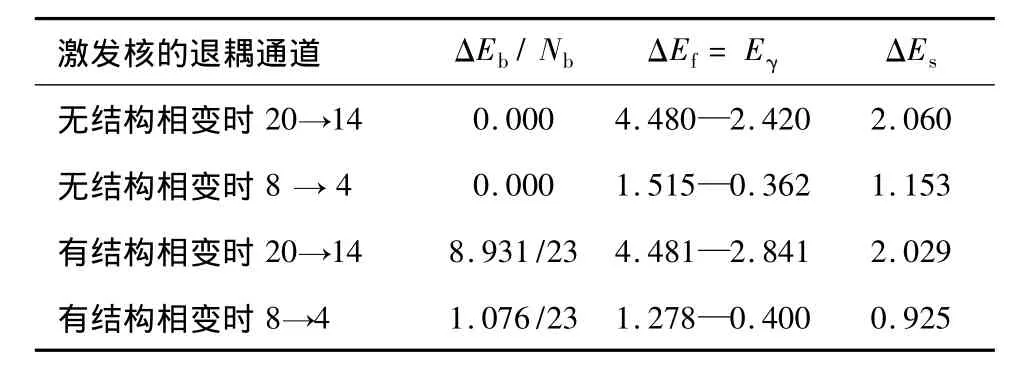
表5182Os核相變時耗能的比較(MeV)

計算結果顯示(見表4):d-波色子總能量、體系的集體性(有序度)和三個相應基準態的總能量由大到小的排列順序都是:高激發—中激發—低激發.這正是核體系把在被激發時存儲的結構能(成序能)逐級轉化為輻射能以后，才從高激發態退激發到中激發態，最后再到低激發態的.它證實了最初猜想:受激原子核，總是發生從較高激發—較高有序態到較低激發—較低有序態的結構相變.這也可以用相應基準態的總能量差(即成序能差)來加以描述.這樣，核形狀相變理論與朗道經典熱相變理論之間就有了某些相似的描述術語和物理內涵［32，33］.

又從能量的角度看，對于理想波色體系，總體上核體系的總能量Es分為兩部分:能釋放出來的自由部分Ef(輻射能Eγ(I→I－2)=Ef(I)－Ef(I－2)=ΔEf(I))和不能立即釋放的結構束縛能Eb部分(即總結合能，成序能).但是，兩者在結構相變時是能互相轉換的.微觀上，它又是所有玻色子總能量的總和，即

在ΔI=2，

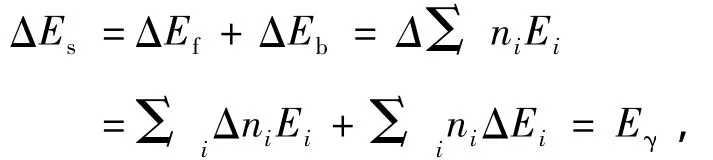
則有

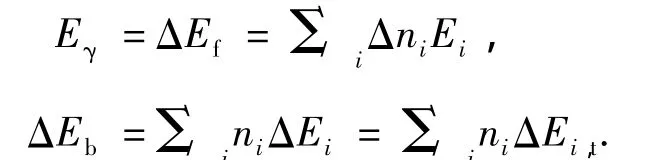
這里Ei，t是第i個玻色子的總結合能.這些等式表明，原子核體系在沒有相變(ΔEb=0)時的被激發或退耦合中，該吸收或釋放的能量Eγ完全用于γ-吸收或輻射;在有相變時，Eγ還與改變基準態結構的用能ΔEb有關，它是ΔEb和ΔEf之和.由于傳輸能量需要時間(有惰性)，從能量源的響應看，核體系在被激發時，激發源以較慢的方式提供最少的能量;但在退耦合中，核子系統又以較慢的方式釋放最少的能量.當被激核退耦到共存區時，基準態結構能的改變小于對應的能級躍遷的能量值，加之有基準態重組的有利條件，因而有足夠的時間完成基準態的結構相變并輻射Eγ;而在非共存區中沒有重組條件，只能以躍遷方式釋放能量.這正是對唯象上“能量有利”解釋的微觀闡述.

表5揭示，在相變共存區，單個核子平均結構能的改變的確很小，結構相變也容易實現;通過結構相變和退耦合方式釋放能量是經濟的.高能激發模式到中能激發模式很光滑，而中能激發模式到低能激發模式卻較為激烈.反過來，在相變共存區，由于核轉動減慢，減小了核子及其核子對之間的相互作用強度，引發組態重組，實現核結構改變.它對單個核子平均結構能的改變雖然很小，可對整個核結合能的改變就很大，即核結合能對核結構極端敏感.這與Cakirli和Casten等［34］的最新工作(核結合能對集體結構高度的敏感)是一致的，對此給出了一個可靠的微觀注釋.

4. 結論

對于一個原子核中發生的從一種激發模式向著另一種激發模式過渡的識別和機理，本文提供了一個新理解:由于退激發能量解除了原有激發模式的基準態結構及其在能量上的優勢，高有序基準態釋放結構能，引發激發模式基準態結構重組，在相變共存區實現新舊激發模式基準態的過渡.對重組過程中的能量關系作了一般性討論，并把這種理解合理地推廣去描述同一核中的兩次RDSPT，使得核形狀相變理論與朗道經典熱相變理論之間有了某些相似的描述術語和物理內涵.最后，以182Os核中發生的SU(3)→O(6)→SU(3)為例作了詳細說明.

［1］Iachello F 2000 Phys.Rev.Lett.85 3580

［2］Iachello F 2001 Phys.Rev.Lett.87 05250

［3］Jolie J，Casten R F，Brentano P von，Werner V 2001 Phys. Rev.Lett.87 162501

［4］Casten R.F 2006 Nature Physics 2 811

［5］Jolie J，Casten R F 2005 Nuclear Physics News 15 20

［6］Niksic T，Vretenar D，Lalazissis G A，Ring P 2007 Phys.Rev. Lett.99 092502

［7］Leviatan A 2007 Phys.Rev.Lett.98 242502

［8］Regan P H，Beausang C W，Zarmfir N V 2003 Phys.Rev.Lett. 90 152502

［9］Meng J，Zhang W，Zhou S G，Toki H，Geng L S 2003 arXiv nucl－th/0312055v1

［10］Zhang Y，Hou Z F，Liu Y X 2007 Phys.Rev.C 76 011305

［11］Liu Y X，Mu L Z，Wei H Q 2006 Phys.Lett.B 633 49

［12］Liu M L 2007 Phys.Rev.C 76 054304

［13］Shen S F，Chen Y B，Xu F R，Zheng S J，Tang B，Wen T D 2007 Phys.Rev.C 75 047304

［14］Leviatan A，Iachello F 2008 arXiv nucl-th/0812.4034v1

［15］Yang S，Philip M.Walker，Xu F R，Liu U X 2008 Phys.Lett. B 659 165

［16］Shi Z Y，Tong H，Shi Z Ya，Zhang C M，Zhao X Z，Ni S Y 2007 Acat Phys.Sin.56 1329(in Chinese)［石筑一、童紅、石筑亞、張春梅、趙行知、倪紹勇2007物理學報56 1329］

［17］Shi Z Y，Zhang C M，Tong H，Zhao X Z，Ni S Y 2008 Acta Phys.Sin.57 1564(in Chinese)［石筑一、張春梅、童紅、趙行知、倪紹勇2008物理學報57 1564］

［18］Wang H，Zhang H，Shi Z Y，Lei Y X，Tong H，2008 Journal of Southwest University(Natural Science Edition)30 48(in Chinese)［汪紅、張歡、石筑一、雷玉璽，童紅2008西南大學學報(自然科學版)30 48］

［19］Shi Z Y，Tong H，Zhang H，Wang H，Lei Y X，Zhao X Z，NI S Y 2009 Acta Phys.Sin.58(in Chinese)［石筑一、童紅、張歡、汪紅、雷玉璽、趙行知、倪紹勇2009物理學報58］

［20］Yang Z S，Liu Y，Qi H 1984 Nucl.Phys.A 421 297

［21］Yang Z S，Liu Y，Tian X Q 1982 High Energy Phys.＆Nucl Phys.6 472(in Chinese)［楊澤森、劉庸、田曉岑1982高能物理與核物理6 472］

［22］Liu Y，Shi Z Y，Dan H J，Sang J P 1995 Chinese Journal of Nuclear Physics 17 194

［23］Shi Z Y，Liu Y，Sang J P 2000 Chin.Phys.9 9

［24］Shi Z Y，Liu Y，Sang J P 2001 Chin.Phys.10 282

［25］Shi Z Y，Zhao X Z，Tong H 2003 Chin.Phys.12 732

［26］Shi Z Y，Ni S Y，Tong H，Zhao X Z 2004 Acta Phys.Sin.53 734(in Chinese)［石筑一、倪紹勇、童紅、趙行知2004物理學報53 734］

［27］Chu S Y，Nordberg H，Firestone R B，Ekstrm L P 2005 Isotope Explorer 3.0//ie.lbl.gov/toi.htm.

［28］Pattison L K，Cullen D M，Smith J F，Fletcher A M，Walker P M，El-Masri H M，Podolyak Z，Wood R J，Scholey C，Wheldon C，Mukherjee G，Balabanski D，Djongolov M，Dalsgaard T，Thisgaard H，Sletten G，Kondev F，Jenkins D，Lane G J，Lee I Y，Macchiavelli A O，Frauendorf S，Almehed D 2003 Phys. Rev.Lett.91 182501

［29］Tandel U S，Tandel S K，Chowdhury P，Cline D，Wu CY，Carpenter M P，Janssens R V F，Khoo T L，Lauritsen T，Lister C J，Seweryniak D，Zhu S 2008 Phys.Rev.Lett.101 182503

［30］Goodman A L 1999 Phys.Rev.C 60 014311

［31］Kaneko K，Hasegawa M，Mizusaki T 2002 Phys.Rev.C 66 051306(R)

［32］Landau L D，Lifshitz E M 1980 Statistical Physics Part 1(3 rdEdition Oxford:Pergamon Press.)p.257—260，p.446—516

［33］Wang Z C 2003 Thermodynamics and statistical physics(3rded. Beijing:Higher education press.)132—140.(in Chinese)

［34］Cakirli R B，Casten R F，Winkler R，Blaum K，Kowalska M. 2009 Phys.Rev.Lett.102 082501

PACC:2110R，2160E，2320L

*Project supported by the Science Foundation of Guizhou Province，China(Grant No:Qian Ke He J Zi:［2009］2071).

?Corresponding author.E-mail:Shizhuyi@vip.sina.com.cn

Nuclear shape phase transition SU(3)→U(5)→SU(3)of the yrast-band structure in182Os from nucleonic order*

Tong Hong1)Zhang Chun-Mei2)Shi Zhu-Yi1)?Wang Hong1)Ni Shao-Yong1)
1)(Department of Physics，Guizhou Institute for Nationalities，Guiyang550025，China)
2)(Department of Basic Science，North University for Ethnics，Yinchuan750021，China)
(Received 9 March 2009;revised manuscript received 6 August 2009)

That quantum phase transition(QPT)that occurs at the same nucleus causing the change of the basic state by rotation can be understood as an evolution from a higher-ordered and high-excitation model to another lower-ordered and high-excitation one，which implies a nucleus populated at high-momentum state decoupling firstly to the yrast-band with some E2-trasitions mode，then to the coexist region(or critical point)，wherein the structure-energy is released.The change of the nucleon coupling intensity is caused，finally the basic state of the lower-ordered excitation model is reconstructed，the evolution of basic states structure is accomplished.This description of nuclear QPTs has endowed them with some similar to Landau’s classical quantum thermal phase transition in terminology and physical significance.This standpoint is generalized into the phase transitions that occur at the same nucleus one after an other.As an example，for the182Os nucleus，the problem is discussed carefully，and the enhanced sensitivity of nuclear binging energy to collective structure is demonstrated.

quantum phase transition，evolution of yrast－band structure，microscopic sdIBM-珔Fmaxapproach，182Os nucleus

book=243,ebook=243

*貴州省科技廳自然科學項目(批準號:黔科合J字:［2009］2071號)資助課題.

?通訊聯系人.E-mail:shizhuyi@vip.sina.com.cn