基于小波變換的自適應圖像去噪研究*

鄭州大學西亞斯國際學院 葛明濤 樊永良 董素鴿

基于小波變換的自適應圖像去噪研究*

鄭州大學西亞斯國際學院 葛明濤 樊永良 董素鴿

小波域的信息處理有多分辨率分析的特性，圖像經一系列小波變換就可以得到不同尺度下的圖像特征，并能較好地刻畫圖像的非平穩性，在圖像去噪方面有著傳統去噪方法無法比擬的優勢。本文，筆者闡述了圖像小波去噪的原理，分析了影響去噪的關鍵因素、閾值函數的構造、閾值的選取及小波的分解層數等，并給出了優化的自適應圖像去噪方案。

一、圖像去噪方法

1.常用的圖像去噪方法。圖像去噪是圖像處理的重要環節，關系到圖像處理的質量。常用的圖像去噪方法可分為基于空域的方法和基于變換域的方法。前者是對原圖像素點的灰度值進行數據處理，典型的方法有中值濾波、均值濾波等，但這些方法往往會在去除噪聲的同時引起圖像邊緣和細節模糊等問題。變換域去噪是將原定義在空域的圖像以某種形式轉換到其他空間，并利用這些空間的特有性質對變換后的圖像信息進行處理，再反變換回圖像空域。常用的方法是傅立葉變換去噪，該方法采用低通濾波來平滑抑制噪聲，但在去除噪聲的同時也會把圖像的邊緣變模糊。

2.變換域小波域去噪法。變換域小波域去噪是利用含噪圖像在小波域中信號與噪聲在小波系數上存有差異這一特點而實現的，即圖像邊緣（信號的突變點）對應的小波系數極大值隨著分解尺度的增大而增大，而噪聲（以白噪聲為例）對應的小波系數極大值隨著尺度的增大而減小。當分解尺度增大到某個尺度時，絕大部分白噪聲對應的小波系數極大值因衰減而消失，該情況說明信號的能量集中于少數較大的系數上，而噪聲則主要表現為小系數。因此，通過選取合適的閾值，將絕對值小于閾值的小波系數作為噪聲去除，從而達到去噪的目的。小波的不同分辨層次所體現的多分辨率特性使得圖像的輪廓信息可以在低分辨率下通過提取邊緣信息來獲得，紋理信息則可在較高的分辨率下表現。所以，小波域圖像去噪能更多地突出圖像的邊緣特性。

二、圖像的小波域變換

一了各種具體的小波的構造方法，并于1987年提出了著名的小波分解與重構的塔式算法。只要將該方法推廣到二維空間，即可應用到圖像的分解與重建上。為此，我們將圖像視為一個能量有限的二維函數f（x，y）∈L2（R2），對于可分離的L2（R2）多分辨率空間，設ψ（x，y）為一維母小波，對應的尺度函數為φ（x，y），x、y分別代表橫坐標和縱坐標，則有：

對應二維平面的3個方向：水平、垂直和45°方向。3個方向的二維小波函數為：

在x方向上分別用φ（x）和ψ（x）作分析，把f（x，y）分解成平滑逼近和細節兩部分，再分別對其沿y方向上作類似分析。這樣多分辨率小波變換就可以把圖像分解到更低分辨率的水平上，這一級的子圖像由低頻的輪廓信息和原信號在水平、垂直和對角線方向上的高頻部分的細節信息組成。每一次分解均使得圖像的分辨率變為原信號的1/2。對于二維離散小波變換，其分解公式為：

Ajf（x，y）=[f（x,y）,2-jφ（2-jx-n）φ（2-jy-m）]，（5）辨

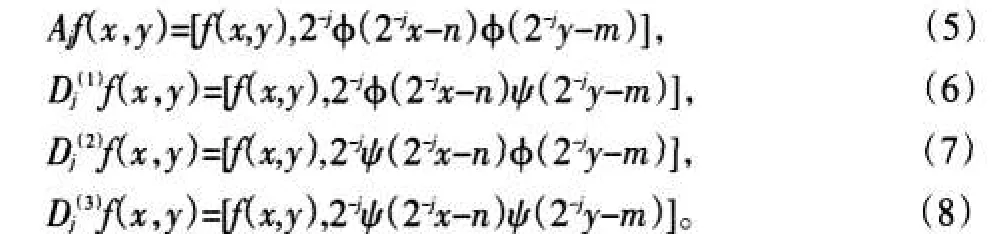
率的低頻輪廓信息，D（1）2n f為垂直方向的高頻細節信息，D（2）2n f為水平方向的高頻細節信息，D（3）2n f對角線方向的高頻細節信息。經過二維小波變換，將原圖像逐級分離成具有不同尺度的子圖像，其中包含4個分量：低頻分量LL，保留了原圖的大部分信息；高頻分量LH、HL、HH均包含了邊緣、區域輪廓等細節信息。同時LL還可以進行第j+1級小波分解，以得到下一級分辨率下的圖像表示。圖像的3級小波分解見圖1。

S.Mallat提出的小波多分辨率概念，在泛函分析的框架下統

三、小波閾值去噪

1.小波閾值去噪的步驟。含噪信號的數學模型可描述為：

f（k）=s（k）+n（k）。（9）

圖1 圖像的3級小波分解

其中，f（k）為待測信號，s（k）為原始信號，n（k）為高斯白噪聲信號，滿足n（k）～N（0，δ2）的正態分布。可見去噪問題即為如何在信號f（k）中去除噪聲n（k），同時盡可能多地保留s（k）信息。根據上述小波去噪的原理，采用閾值消噪的一般步驟是：

（1）選擇合適的小波基Φ（x）及相應的分解尺度j，對含有噪聲的信號進行二進離散小波變換，得到各尺度上的小波系數Cj，k。

（2）選擇合適的閾值T及相應的閾值處理函數g（Cj，k，T）對小波系數進行處理，得到處理后的系數j，k=g（Cj，k，T）。

（3）對處理后的系數j，k進行小波重構，得到信號s的近似信號s。

2.閾值函數及閾值的確定。由以上小波閾值去噪的步驟可以看出，小波閾值去噪的關鍵是如何使近似信號s更逼近原信號，即如何最大程度的濾除噪聲信號n，同時盡可能多地保留信號s的信息。因此，小波閾值去噪的關鍵是如何選取門限閾值及閾值處理函數。

Donoho提出了基于軟閾值和硬閾值的小波去噪算法，該方法設計的閾值函數計算簡單。硬閾值法是將模小于閾值的小波系數Cj，k置0，保留模大于閾值的系數，即，

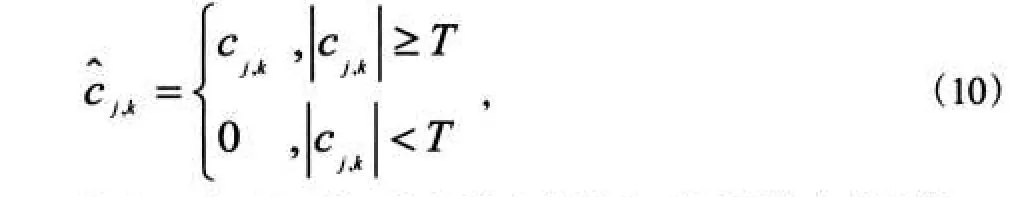
置0，而將模大于閾值的系數做了向0的收縮，即，它在

T處的不連續性，會使圖像出現振鈴、偽吉布斯效應等視覺失真。而軟閾值函數j，k連續性好，處理結果則相對平滑。但當j，k＞T時，j，k與Cj，k總存在恒定的偏差T，這樣就會影響重構信號與真實信號的逼近程度，造成邊緣模糊等失真現象。實驗中采用模糊閾值函數算法解決該問題，其軟閾值函數構造如下：

其中，K為模糊函數1/[1+Cj，k-T]，當|Cj，k|=T時，K=1，j，k= |Cj，k|-T，使整體連續性得到了保證，從而避免了信號產生振蕩；當|Cj，k|＞T時，K＜1，Cj，k與j，k的偏差小于T，而且|Cj，k|越大，Cj，k與j，k的偏差越小，重構信號與真實信號的逼近程度越高。

Donoho等人提出的VisuShrink方法，給出的閾值T按照如下的公式選取：

其中，N為信號的尺寸或長度，σ是噪聲的標準差。

不論軟閾值或硬閾值,其中所用的閾值均為全局閾值，即無論小波分解層數為多少，每層閾值均相同且固定不變，對于不同的分解尺度而采用相同閾值顯然是不合適的。全局閾值雖然可以取得一定程度上的抑噪效果，但由于其單一性，而不能在每個尺度上都最大限度地分離圖像和噪聲。

由上所述，隨著分解尺度的增大噪聲的幅值是變小的，而信號幅值恰好相反。根據小波系數的特點實驗中采用自適應閾值，其表達式如下：

可以看出隨著分解尺度j的增大，閾值是逐漸減小的，這一點正好符合上述規律。

3.分解層數的選擇。信號小波分解的層數對去噪也會有一定的影響，從實驗結果的對比得到的結論為：對圖像的小波分解最佳層數為3層。該結論雖沒有得到理論上的證明，但分析其實驗數據可知去噪后信號的信噪比隨著分解層數的增加而迅速增加。在超過3層之后，去噪后信號的信噪比沒有太大的變化，且分解層數的增大將帶來更大的計算量。

四、實驗與結果分析

為驗證以上分析，對標準的“Leda”圖像（512×512×8bit）加入不同方差的高斯白噪聲，并用傳統的去噪方式與自適應小波去噪方式、優化閾值函數和自適應閾值的小波去噪方式進行比較。實驗中的小波為正交小波Daubechies-4，小波分解層數為3層，采用峰值信噪比（PSNR，Peak Signal-to-Noise Ratio）這一客觀標準作為性能評價指標，實驗結果如表1。

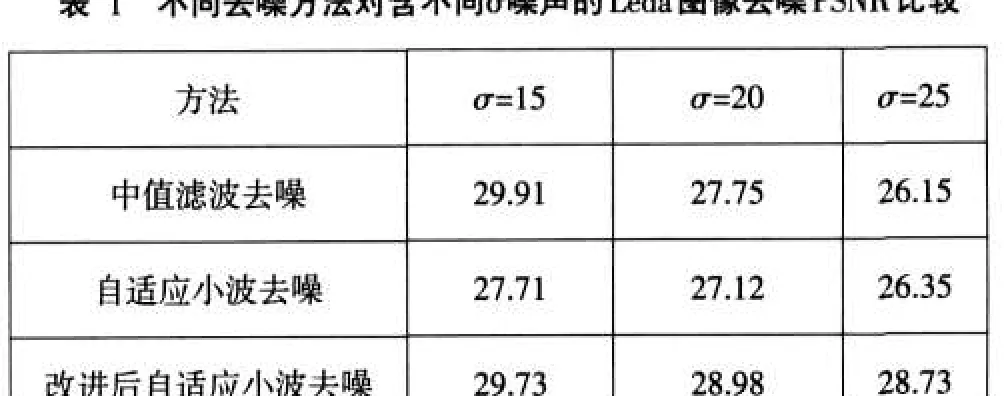
表1 不同去噪方法對含不同σ噪聲的Leda圖像去噪PSNR比較

由上表可知，隨著噪聲強度的增大，改進后自適應小波去噪方法的效果要更優于前2種方法。

圖像的去噪，是為之后的圖像信息壓縮編碼等工作奠定基礎的。筆者根據小波去噪的特點，提出了較為綜合的小波域去噪方法，通過實驗數據對比，表明小波域去噪效果較好。由于實驗中僅以白噪聲為干擾信號，那么，根據不同噪聲的統計特性設計濾波器將是下一步設計的方向。

河南省教育廳2010年科技攻關項目