底棲生物生物量空間插值方法研究

張偉，李純厚，賈曉平，陳丕茂，方良

(中國水產科學研究院南海水產研究所、農業部海水養殖生態與質量控制重點開放實驗室、農業部南海漁業資源重點野外科學觀測試驗站，廣東 廣州 510300)

底棲生物生物量空間插值方法研究

張偉，李純厚，賈曉平，陳丕茂，方良

(中國水產科學研究院南海水產研究所、農業部海水養殖生態與質量控制重點開放實驗室、農業部南海漁業資源重點野外科學觀測試驗站，廣東 廣州 510300)

在地統計學和地理信息系統支持下，采用反距離加權(Inverse distance weighting，IDW)、徑向基函數(Radial basis functions，RBF)、普通克里格 (Ordinary Kriging，OK) 3種插值方法對2007年4月獲得的大亞灣人工魚礁區及附近海域底棲生物生物量數據進行空間插值方法研究，并對插值精確度進行交叉驗證。結果顯示，經對數轉化后的數據呈正態分布，而且3種插值方法對其進行插值，所得的等值面圖效果比原始數據所得等值面圖效果好。交叉驗證顯示，對數轉化數據插值精確度OK＞RBF＞IDW。觀察插值結果等值面圖，發現3種方法均能較客觀地模擬出底棲生物生物量的總體分布趨勢，在對局部趨勢的模擬上，OK的表現效果最好。

底棲生物生物量；空間插值；研究

底棲生物是水生態系統的重要組成部分，是海洋中各種魚類生長和繁殖的餌料基礎，是海洋生態動力學研究的重要對象[1]。因此研究水域中底棲生物的資源狀況，對于深入探討水域生態環境、水生生物區系、群落組成和魚類資源變化都有重要的科學價值和實際意義。

地理信息系統(GIS)具有很好的空間數據處理和分析功能，如它提供的地統計方法就是一種全新的解決問題的方案，空間插值是其重要的功能之一。ArcGIS地統計分析模塊在地統計學與GIS之間架起了一座橋梁。使得復雜的地統計方法可以在軟件中輕易實現。體現了以人為本、可視化發展的趨勢。

空間插值法可以用已知的空間數據估計（預測）未知空間的數據值[2]，它已經用于很多領域的研究中，如：氣象[3,4]、降雨[5,6]、土壤[7]等。這些領域都進行了空間插值的比較研究，但是對于海洋底棲生物的研究還鮮有報道。因此，本文進行了初步的嘗試，利用2007年4月在大亞灣所設的12個站點的底棲生物生物量數據資料進行空間插值方法研究，探討不同種類插值方法的應用效果，以為今后底棲生物插值方法的應用起到一定的參考作用。

1 材料與方法

1.1 數據來源

采用2007年4月，在深圳楊梅坑人工魚礁區及附近海域（22°32.94′—22°34.98′N，114°34.48′—114°36.57′E），設12個站位進行底棲生物調查。調查站位設置見圖1。底棲生物的采集和分析均按《海洋監測規范》[8]（GB17378－1998）和《海洋調查規范—海洋生物調查》[9]（GB12763.6－91）中規定的方法進行。本文采用底棲生物生物量數據進行空間插值方法研究。

1.2 GIS軟件與統計軟件

軟件采用美國環境系統研究所 (ERSI) 的GIS桌面平臺系統ARCGIS 9.2，選用SPSS13.0以及EXCEL 2003作為數據統計分析的工具。利用地理信息系統軟件ARC/INFO 9.2的空間分析模塊(Spatial Analyse) 和地理統計模塊 (Geostatistical Analyst)[10,11]提供的3種插值方法：反距離加權法、徑向基函數法和普通克里格法。

1.3 探索性空間數據分析和數據轉化

1.3.1 數據分布檢測 數據檢測，即空間數據探索分析（ESDA）。ARC/INFO 9.2提供了多種檢測數據分布特征的方法。對于正態分布，有一個快速檢驗的方法：如果平均值與中值大致相等，就可以把它當作數據服從正態分布的證據之一。另一種檢驗方法是正態QQ圖,檢查數據的正態分布情況。其作圖原理是用分位圖思想，直線表示正態分布，如果數據接近一條直線，則它們越接近于服從正態分布。

1.3.2 數據轉化 很多插值和統計分析方法要求數據符合正態分布[11]。根據探索性空間數據分析得到的數據性質，選擇合適的轉化方法，可使數據基本上符合正態分布。通過分析，得出對原始數據進行對數轉化，可使轉化后的數據呈正態分布。

1.4 空間插值方法

目前，用于海洋底棲生物的空間插值方面的研究鮮見報道，本研究主要采用反距離加權插值法、徑向基函數插值法和普通克里格3種方法。

1.4.1 反距離加權法 反距離加權（inverse distance weighted,IDW）插值法基于相似原理，即兩個物體離得越近，它們的性質就越相似；反之，離得越遠則相似性越小。它是最常用的空間內插方法之一，

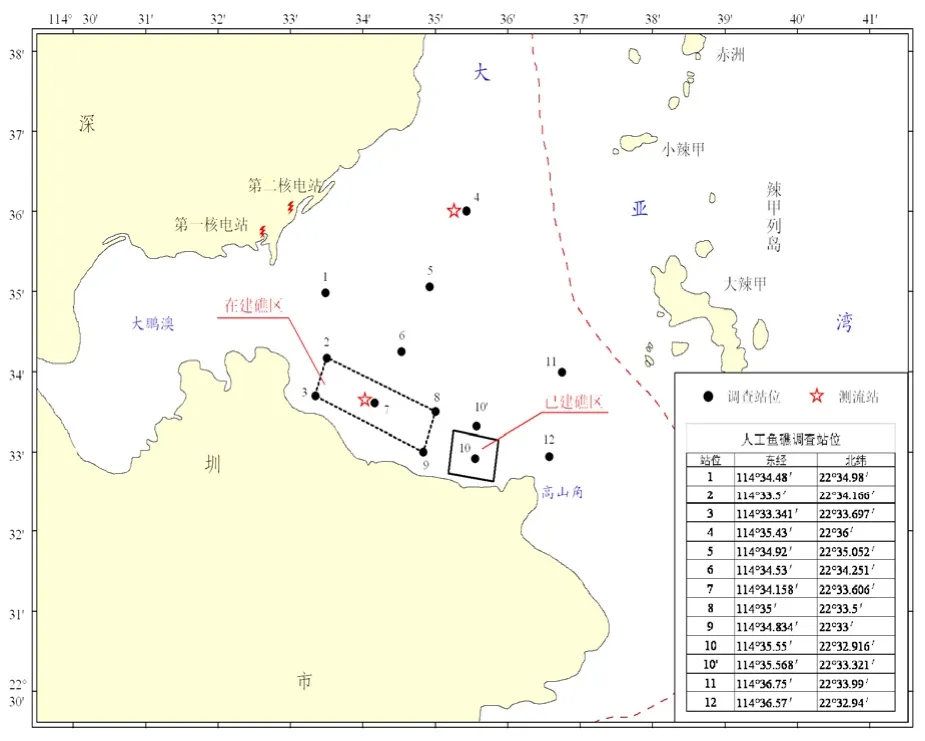
圖1 大亞灣底棲生物調查站位示意圖Fig. 1 Sampling stations of Macrobenthic in the Daya Bay

式中：Z為估計值，Z為第i (i=1，…，n)個樣本，Di為距離，P為距離的冪，其顯著影響內插的結果，它的選擇標準是最小平均絕對誤差。

這種空間插值方法的優越性是直觀并且效率高，在已知點分布均勻的情況下插值效果好。

1.4.2 徑向基函數插值法 徑向基函數法是人工神經網絡方法中的一種。由徑向基函數生成的表面不僅能夠反映整體變化趨勢，而且可以反映局部變化。當取樣點擬合的曲面不能準確地代表表面時，可以采用徑向基函數法。

1.4.3 克里格插值法 克里格（Kriging）插值法是空間統計分析方法的重要內容之一，它是建立在半變異函數理論分析基礎上的，是對有限區域內的區域化變量取值進行無偏最優估計的一種方法。Matheron[12]給出了克里格法的一般公式：

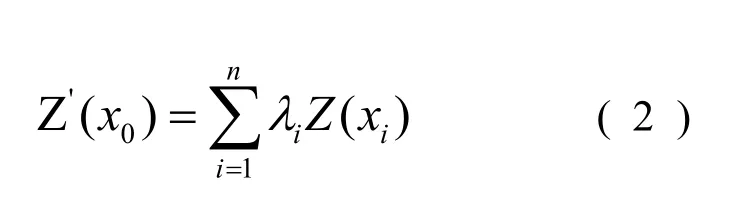
即

選取iλ，使的估計無偏，并且使方差2iσ小于任意觀測值線形組合的方差。

克里格方法進行插值時，不僅考慮了待預測點與鄰近點數據的空間距離關系，還考慮了各參與預測的樣點之間的位置關系，充分利用了各樣點數據的空間分布結構特征，使其估計結果比傳統方法更精確，更符合實際，更有效地避免了系統誤差的出現。

1.5 驗證方法

采用交叉驗證法 (cross validation) 來驗證插值的效果。對于每一種插值法，交叉驗證分析重復從已知數據集中刪除一個采樣點的過程，用剩下的采樣點估算被刪除點的數值，并計算誤差均值(MEAN) 和誤差均方根 (Root-Mean-Square,RMS)。一般來說，各種插值方法的誤差均值絕對值和誤差均方根總體最小者，具有較好的插值效果，尤其是RMS越小越好[13]。

2 結果分析

2.1 數據分布

人工魚礁區12個站位底棲生物生物量的平均值為48.05g/m2，中值為21.45 g/m2，兩者差別比較大，不屬于正態分布；正態QQ圖上，12個站位生物量基本上不在一條直線上，因此，也不屬于正態分布。

上述兩種方法所得出的結果都表明12個站位底棲生物生物量都不接近正態分布。因此，對其分析時，要進行數據轉化。

2.2 數據轉化

對數據變換會使數據更趨于正態分布并且會提高預測的精度[14,15]。很多學者運用對數、立方根、平方根等變換方式對數據進行預處理以提高插值的精度。研究中我們在對樣本數據進行分析的基礎上對其進行了變換方式的優化選擇，結果表明：經過對數轉換后的數據從整體上更趨向于正態分布，原始數據和對數轉化后數據的正態分布見圖2所示。因此，在整個分析過程中，對底棲生物我們均采用了原始數據與對數變換兩套數據，并對其插值結果進行了對比分析。

2.3 插值結果與分析

插值方法的比較分析采用了反距離權重法、徑向基函數和普通克里格法。反距離權重法的距離權重指數為2，站點搜索范圍為臨近的12個站點；徑向基函數，站點搜索范圍為臨近的12個站點；克里格法的半方差函數分兩種情況：原始數據采用圓形模型(#KRIGING_CIRCULAR)，而對數轉化數據采用高斯模型（#KRIGING_GAUSSIAN）,站點搜索范圍也為臨近的12個站點；各種插值方法在檢驗站點的結果誤差如表1。

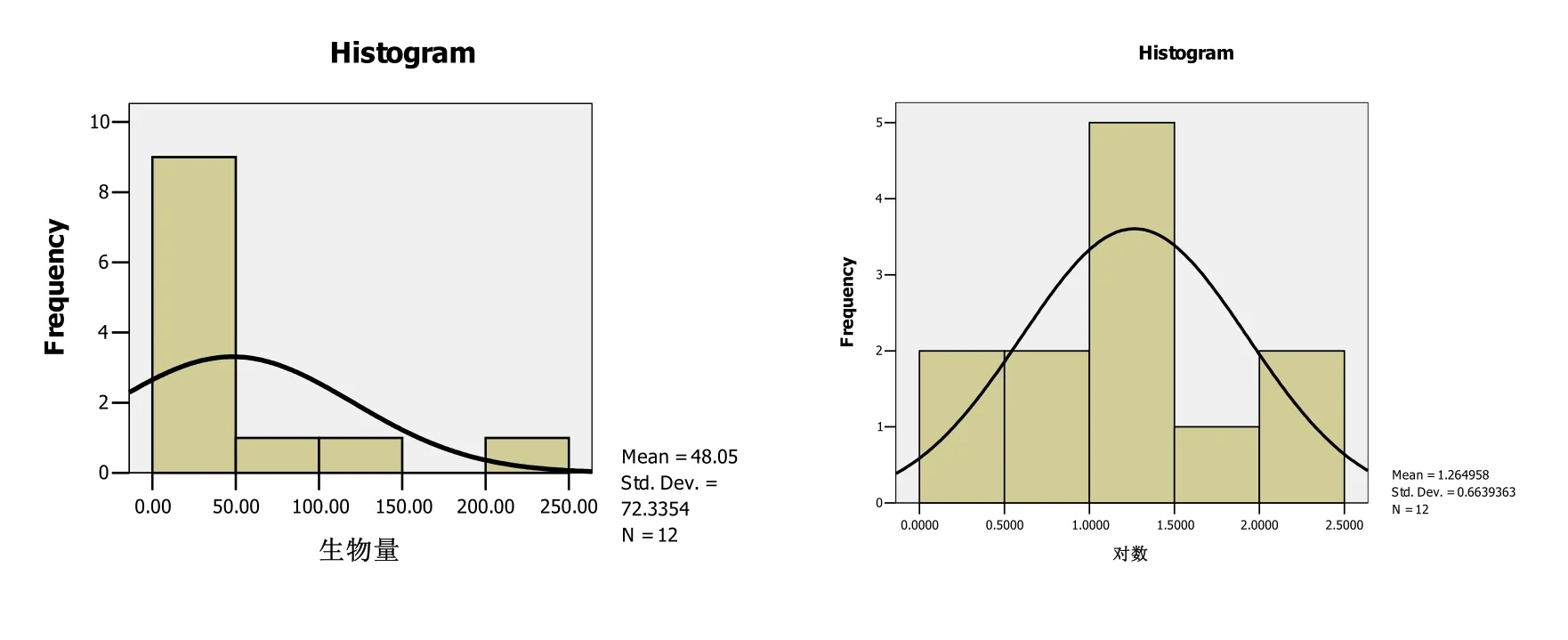
圖2 底棲生物生物量原始數據和對數轉化數據分布圖Fig. 2 Distribution map of raw and log-transformed data of Macrobenthic biomass

2.3.1 數據轉化對插值結果的影響

表1表明，在數據轉化后，3種方法的MEAN和RMS絕對值均有所下降，充分顯示出數據經過轉化后，精度明顯上升，而且上升幅度比較大。通過采用3種方法比較發現，使用原始數據進行插值分析時，IDW和RBF的插值效果均比OK 的插值效果好。而經過對數轉化以后，對其進行插值分析，OK的插值效果比IDW和RBF的插值效果好。同時，從插值結果等值面圖來看（圖3），轉化基本消除了由于極大、極小值引起的小等值線圈、尖銳的等值線鋸齒、缺刻等插值噪音，使底棲生物生物量的平面分布趨勢更明晰易辨。

表1 不同插值方法得到的誤差均值和誤差均方根Tab. 1 MEAN and RMS calculated by different interpolation methods

2.3.2 不同插值方法比較 以轉化后數據的插值結果作為不同方法比較的依據。

由表1可見，3種方法得到的誤差均值絕對值和誤差均方根的大小順序均為OK＜RBF＜IDW，說明3種方法對大亞灣底棲生物生物量數據的插值精確度，OK最高，RBF次之，IDW最低。然而，通過RMS比較，發現兩種方法得出的結果都具有較高的精度，僅 IDW和RBF略遜于OK。這是因為OK法在插值過程中充分利用了數據點之間的空間相關性。但從整個插值計算過程來看，IDW和RBF比OK要相對簡單。表明此3方法在底棲生物插值模型中均能獲得較好效果。

一方面，從整體上觀察使用3種方法得到的空間插值圖（圖3），底棲生物分布的基本趨勢是一致的，都是附近海域的平均生物量最高，平均生物量最低為在建礁區。因此，可以說這3種插值方法都基本上表明底棲生物的空間分布趨勢。

另一方面，從較小的空間尺度觀察插值平面（圖3），發現IDW生成的等值線往往會圍繞生物量值極大或極小的采樣點發生大曲率的彎曲，甚至閉合形成小等值線圈，說明IDW對極端值敏感，這會對整體趨勢產生干擾。RBF適用于對大量點數據進行插值計算從而獲得平滑表面，這樣能夠很好的反映整體變化趨勢。但是忽略了對較小空間尺度變化趨勢的表現。只有OK，既具有高耐抗性，又能在等值線的平滑度與精確度之間達到較好的平衡，對總體趨勢與局部趨勢都有良好的表現。

綜上所述，以上3種插值方法，都能很好的模擬出底棲生物的分布趨勢，而從較小的空間尺度看，結合交叉驗證的結果，OK的插值效果是最好的，是最適合用于底棲生物生物量數據的插值方法。

3 討 論

影響底棲生物空間插值精度的因素主要有2個，一個是插值方法本身引起的誤差，如在插值過程中插值方法的選擇、各參數的選取等。另一個是外界因素對底棲生物的影響而引起的誤差，如經緯度、離岸距離、沉積環境、人為擾動、頻繁漁業、底棲生物站點的數目和分布狀況、觀測數據本身的誤差等。

空間內插是地學中尤其是資源、環境和生態研究中極為重要的一種空間分析方法。空間內插是研究區域變量空間分布的基本方法，應該充分利用空間插值技術獲取更多精確數據，尤其是對于站點稀少，而站點分布又不合理的地區。同時，選擇合適的插值方法也要結合數據本身的特點和空間特性，并不是越復雜的方法就一定能產生越好的估值效果。各種方法都有其特定假設、適用范圍、算法和優缺點，對于眾多的空間內插方法而言，沒有絕對最優的空間內插方法，只有特定條件下的最優方法。

對深圳楊梅坑人工魚礁區及附近海域底棲生物而言，3種插值方法中，IDW和RBF的插值效果基本一致，而OK的插值效果是最好的，這一研究結果與林琳[16]等的研究結果基本一致。但是IDW和RBF操作起來比較簡單，而OK則需要耗費大量的時間在分析原始數據和半變異函數的訓算和理論模型的擬合建立上，而且其數學過程相對復雜，運算耗時也長。在研究目的許可的情況下，簡單、靈活的IDW、RBF也是合適的選擇。如果需要利用插值結果進行更精細，更高級的空間分析，如圖形疊加、構建生態系統模型等，則必須選擇插值精度最高、對小空間尺度表現最好的插值方法，因為誤差會發生上行傳遞和放大，造成更深遠的影響[17]。

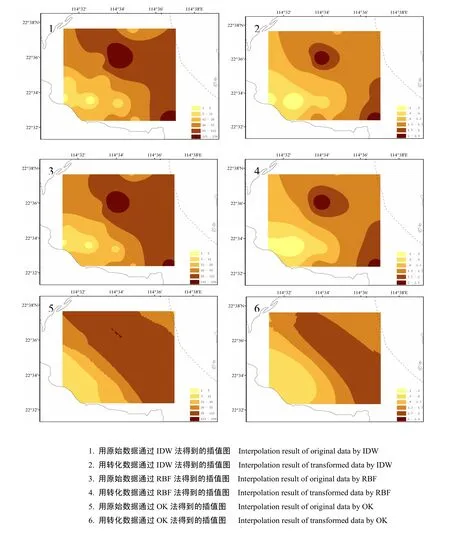
圖3 大亞灣底棲生物生物量的插值結果等值面圖Fig. 3 Interpolation result of the Macrobenthic Biomass in the Daya Bay

底棲生物空間插值中應關注站點數量、分布狀況以及適合數據本身特點的插值方法。時空尺度帶來的不確定性都可歸結為站點數量能否充分反映底棲生物的時空變異特征，所以增加站點數量是提高插值精度的關鍵之一，而插值方法的選擇以及參數的設置也要根據具體的數據情況進行詳細的分析，從而使插值得到最好的效果。

該文初步嘗試應用底棲生物生物量數據進行了3種插值方法應用效果的對比分析，得出OK的插值效果是最好的，是最適合用于底棲生物生物量數據的插值方法。為今后底棲生物的研究提供了一種方法學的指導，然而，空間插值方法在底棲生物中的應用還處于起步階段，還需要做更深入的研究。

[1] 唐啟升. 中國海洋生態系統動力學研究. 北京: 科學出版社,2000.

[2] 李新, 程國棟, 盧玲, 等. 空間插值方法比較 [J]. 地理科學進展,2000, 15(3): 260-265.

[3] 李軍龍, 張劍, 張叢, 等. 氣象要素空間插值方法的比較分析[J]. 草業科學, 2006, 23(8): 6-11.

[4] 封志明, 楊艷昭, 丁曉強, 等. 氣象要素空間插值方法優化 [J].地理研究, 2004, 23(3): 357-364.

[5] 劉胤雯, 賴格英, 陳元增, 等. 梅江河流域年均降雨量空間插值方法研究 [J]. 亞熱帶資源與環境學報, 2007, 2(3): 30-34.

[6] 朱會義, 賈紹鳳. 降雨信息空間插值的不確定性分析 [J]. 地理科學進展, 2004, 23(2): 34-42.

[7] 王秀, 苗孝可, 孟志軍, 等. 插值方法對GIS土壤養分插值結果的影響 [J]. 土壤通報, 2005, 36(6): 826-830.

[8] 國家海洋局. 海洋監測規范. 北京: 海洋出版社, 1991.

[9] 國家海洋局. 海洋調查規范. 北京: 海洋出版社, 1975.

[10] JILL M, KEVIN J. Using ArcGIS Spatial Analyst. CA USA,Redlands, 2001:136-148.

[11] KEVIN J, JAY M H, KONSTANTIN K, et al. Using ArcGIS Geostatistical Anaslyst. CA USA, Redlands, 2001:116-162.

[12] MATHERON G. Principles of geostatistics [J]. Economic Geology,1963, 58: 1246-1266.

[13] 孟慶香, 劉國彬, 楊勤科. 黃土高原降水量的空間插值方法研究[J]. 西北農林科技大學學報(自然科學版), 2006, 34(3): 83-88.

[14] Michael F Hutehinson. Interpolation of rainfall data with thin plate smoothing splines-Part I: two dimensional smoothing of data with short range correlation [J]. Journal of Geographie Information and Decision Analysis, 1998, 2(2): 139-151.

[15] Mare G, Genton. Analysis of rainfall data by robust spatial statistic using s+sPATIALsTATs [J]. Journal of Geographic Information and Decision Analysis, 1998, 2(2): 116-126.

[16] 林琳, 李純厚, 戴 明, 等. 海洋浮游植物豐度的空間插值優化[J]. 生態學報, 2007, 27(7): 2 880-2 888.

[17] Mitas L, Mitasova H. Spatial interpolation methods in GIS. In:Longley P A ed. Geographical information system. volume 1,principles and technical issues, second edition. New Y0rk: Join Wiley & Sons, 1999: 452-461.

Research on spatial interpolation methods of Macrobenthic biomass

ZHANG Wei, LI Chun-hou, JIA Xiao-ping, CHEN Pei-mao, FANG Liang
(South China Sea Fisheries Research Institute; Key Laboratory of Magriculture Ecology and Quality Control, Ministry of Agriculture;Key Field Scientific Experimental Station of South Sea Fishery Resource and Environment, Ministry of Agriculture, Guangzhou 510300, China)

Based on the geostatistical method and GIS, three different methods of spatial interpolation were compared:inverse distance weighting (IDW), radial basis functions (RBF) and Ordinary Kriging (OK), using the recorded Macrobenthic biomass in the artificial reef and nearby sea area of the Daya Bay, China, in April 2007. At the same time,the definition of interpolation was verified by cross-validation. The results showed that after data log-transformed assumed normal distribution, and three kinds of interpolation methods for their interpolation, from the equivalent effect of interpolation surfaces than the raw data by the equivalent effect of contours a good map. The accuracy of the OK was the highest, followed by the RBF, and then the IDW. The interpolation surfaces revealed that all of the three methods correctly showed general trends of the Macrobenthic biomass by using a series of optimization techniques.The generated by the OK were considered the best, as the method could represent both general and local trends accurately.

Macrobenthic biomass；spatial interpolation；research

Q-332; Q178.535

A

1001-6932(2010)03-0351-06

2009-05-27；

2009-07-02

國家863計劃項目（2006AA100303）；科技部科研院所社會公益研究專項資金項目（2005DIB3J020）；公益性科研院所基本科研業務費專項資金項目（2007ZD003）

張偉 (1982－)，女，天津市，碩士，研究方向為漁業環境及其調控。電子郵箱: zhangwei_2004010@163.com