汽車后橋懸架中凸形螺旋彈簧有限元分析

雷鐳，左曙光，楊憲武，王紀瑞，秦立州

LEI Lei, ZUO Shu-guang, YANG Xian-wu, WANG Ji-rui, QIN Li-zhou

（同濟大學 汽車學院，上海 201804）

0 引言

大量早期的汽車設計經驗證明，采用非線性特性的懸架彈性元件可以提高車輛的行駛平順性，已經廣泛采用的空氣彈簧懸架，油氣懸架，橡膠懸架，以及受微機控制的主動式，半主動式懸架都是非線性懸架在汽車上應用的生動例子。近十年來，隨著制造水平的提高，非線性螺旋彈簧開始取代線性螺旋彈簧出現在很多轎車的懸架系統中。非線性螺旋彈簧在汽車上的應用不僅提高了汽車的行駛平順性，同時對汽車的穩定性，安全性都起到了改善作用[1]。相對于前面提到的那些非線性懸架來說，非線性螺旋彈簧懸架在成本，可靠性等方面都有著極大的優勢。因此，對于中低檔轎車而言，采用這種形式彈性元件的懸架必將成為將來轎車懸架設計的發展趨勢 。

帕薩特轎車后橋懸架的彈性元件為中凸形螺旋彈簧，該類型彈簧即屬于非線性彈簧。本文以該彈簧為例，通過有限元分析，對中凸形螺旋彈簧的剛度進行了分析。

1 中凸形螺旋彈簧3D模型的建立

由于通過逆向工程技術來建立實體模型具有精度和效率都高的優點，本文對中凸形螺旋彈簧模型的建立亦采用此方法[3,4]。

1.1 點云采集

將待測量的中凸形螺旋彈簧固定在水平面上。檢查掃描頭在空間的位置，以確定有效的掃描范圍。手持激光掃描頭沿著彈簧絲從上至下螺旋掃描。在掃描過程中，激光斑點和激光帶盡量正對工件表面并處在重合位置，并觀察屏幕實時顯示的結果以確保測量的完整性。為了保證點云質量，對未掃描到的部位重復掃描。

1.2 點云處理

由于測量所得的點多而密，并且雜亂無章。如果直接用于彈簧的曲面建模，會造成點云數據龐大，影響工作效率，所以必須將得到的點云進行數據處理。點云處理包括點云優化、點云過濾及生成三角化網格。點云優化的作用是過濾噪聲點。利用光學測量系統測得的點云在測量方向上是有一定范圍內的跳動的，通過點云優化，可以優化這些跳動點的分布。點云過濾的作用是在保持所有特征的情況下減少數據量，以滿足后續曲面重構的要求。生成三角化網格可直接用于快速成型及生成加工代碼，如圖1所示。

圖1 三角化網格的彈簧模型

1.3 逆向建模

將三角化網格的彈簧模型導入PRO/E軟件中。通過提取彈簧簧絲中心螺旋曲線及簧絲直徑，則可以建立中凸形螺旋彈簧的實體模型，如圖2所示。將建立的中凸形螺旋彈簧實體模型與點云作對比，可知最大誤差為0.0218mm。最大誤差出現在彈簧的底部。由于彈簧底部受水平面阻擋，激光探頭未能完全掃描到此處。

圖2 中凸形螺旋彈簧實體模型

2 中凸形螺旋彈簧的有限元計算

逆向建模所得中凸形螺旋彈簧的結構參數見表1。為了便于加載和約束，彈簧上下端各加有一個法線與彈簧軸線平行的剛性平面。

表1 中凸形螺旋彈簧的結構參數

2.1 網格劃分

由于彈簧模型為三維實體模型，所以在有限元分析中需要選擇三維單元來劃分網格。本文采用六面體8節點HEX8單元為中凸形螺旋彈簧劃分網格，因為HEX8單元沒有四節點四面體那樣剛硬，所以使有限元模型劃分的網格更規則。受力變形均勻且協調一致，從而使計算結果具有較高的計算精度。劃分網格后的模型共計27486個單元，31694個節點，如圖3所示。

圖3 劃分好網格的彈簧模型圖

2.2 定義材料特性

在有限元分析中，定義材料屬性中楊氏模量E=206GPa，泊松比v=0.3，材料密度為7.8x103Kg/m2。

2.3 定義接觸體

定義三個接觸體：由所有彈簧單元組成的可變形體、上下兩個剛性平面。

2.4 約束與加載

在下剛性平面施加六個自由度的全約束，上剛性平面除垂向Z軸位移的五個自由度也受到約束。上剛性面受到載荷為0～6KN的垂向載荷，如圖4所示。

圖4 彈簧模型的約束與加載圖

最后定義好有限元作業的參數即可得到彈簧有限元計算結果，如圖5所示。

圖5 彈簧有限元計算結果圖

通過以上有限元分析計算，可提取出中凸形螺旋彈簧的變形量與載荷之間的關系曲線圖。從圖6可得知，中凸形螺旋彈簧彈簧具有一定的非線性。當彈簧所受載荷較小時，隨著所受載荷的增大，彈簧變形量線性變化。當載荷繼續增大時，彈簧并圈會逐漸增加，相應的有效圈數會減少，無效圈數因此而增加，則彈簧變形量開始呈非線性增加。由于彈簧所有有效圈不可能同時全部降到底部，因并圈而使有效圈數逐漸減少，從而產生的末端效應對彈簧載荷-變形曲線的非線性特性的影響是不可低估的。該彈簧的剛度特性滿足了汽車懸架的彈性元件剛度可變的需要。

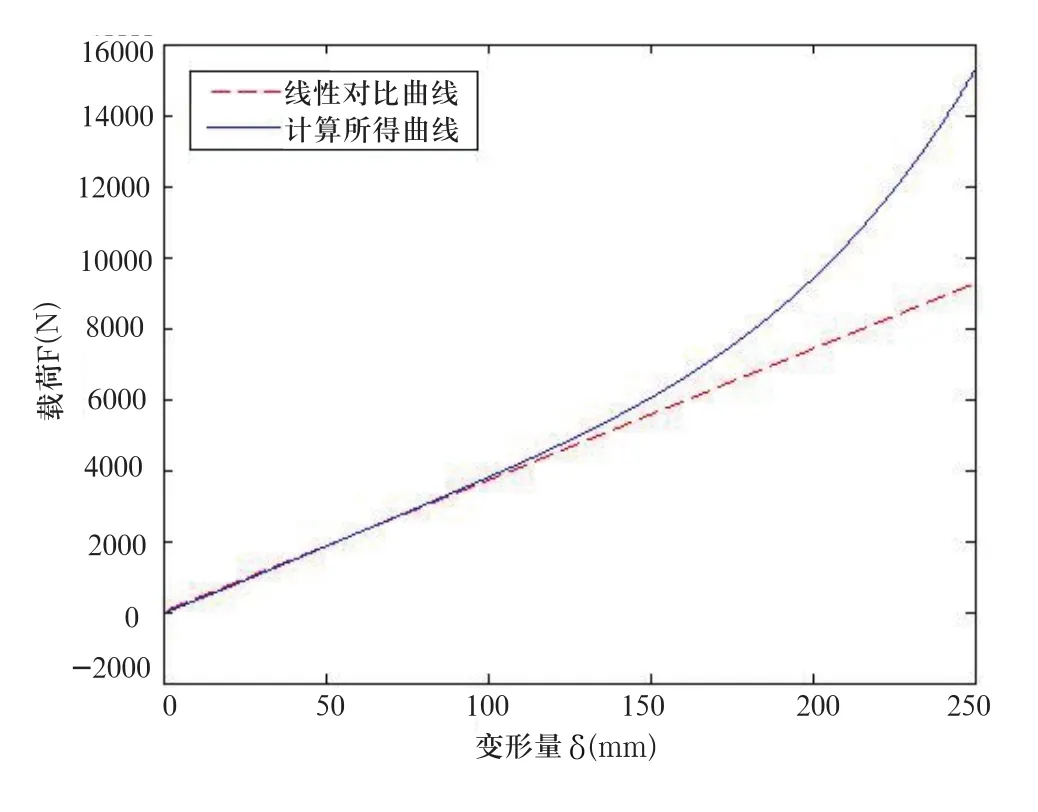
圖6 彈簧變形量與所受載荷的關系圖

提取有限元計算所得載荷F和變形量δ的數據，通過數據擬合，可以得到中凸形螺旋彈簧的剛度公式為：

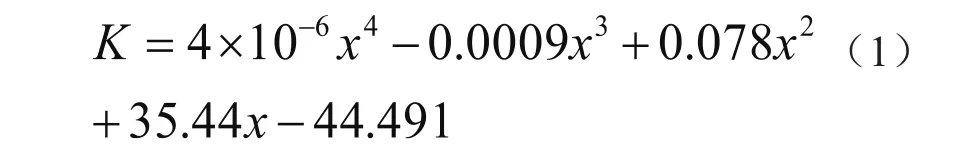
其中

K－中凸形螺旋彈簧剛度（N/mm）

K－中凸形螺旋彈簧變形量（mm）

3 結構參數對中凸形彈簧剛度的影響分析

按照上述有限元分析過程，變化某一結構參數，保持其它參數不變。在中凸形彈簧剛度保持線性區域進行了四組有限元計算以分析其剛度特性。

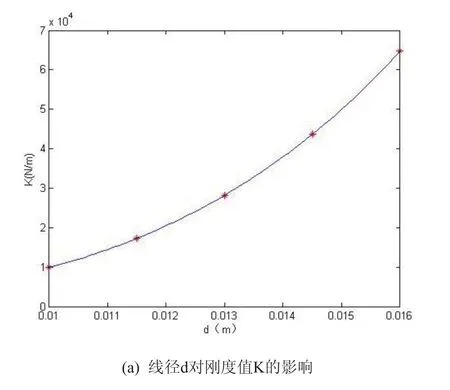
圖7 各參數對剛度值的影響趨勢圖

從圖7中可以看出，隨著線徑d值增大，剛度值K呈非線性增大；隨著最小直徑D2增大，剛度值K非線性減小；隨著最大直徑D1增大，剛度值K非線性減小；隨著有效彈簧圈數n的增大，剛度值K非線性減小。在上述各參數中，隨著線徑d增大，彈簧剛度K迅速增大，而其他參數對剛度影響范圍變化不大，所以彈簧線徑對彈簧剛度的影響顯著。

4 試驗驗證

對樣品彈簧在裝有力和位移傳感器的液壓缸上進行靜力加載試驗，如圖8所示，測得中凸形螺旋彈簧在垂直方向的載荷和變形量的關系曲線，并與有限元仿真結果進行了比較，如圖9所示。通過對比分析可知，所建有限元模型的剛度特性與試驗數據相符，證明有限元分析過程合理、結果較為精確。

圖8 試驗安裝圖

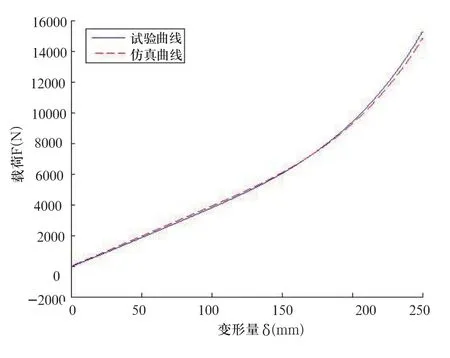
圖9 仿真結果與試驗數據對比圖

5 結論

本文通過逆向工程技術對中凸形螺旋彈簧進行了三維實體建模，并用有限元軟件分析了該彈簧的剛度特性，得到了如下結論：

1）通過逆向工程技術建立的中凸形螺旋彈簧的3D實體模型較為精確。保證了后續有限元分析結果具有較高的計算精度。

2）通過有限元Marc軟件分析計算，可得知中凸形螺旋彈簧具有非線性的特性。該特性使得汽車的行駛平順性和穩定性得到了改善。

3）隨著線徑d值增大，剛度值K呈非線性增大；隨著最小半徑R1、最大半徑R2和有效彈簧圈數n增大，剛度值K非線性減小。其中線徑d對彈簧剛度值的影響最明顯。

4）通過試驗驗證，可知有限元分析結果較為精確。本文的研究結果和分析方法可作為進一步優化中凸形螺旋彈簧設計的基礎，以滿足汽車懸架彈性元件設計的需要。

[1]Y Lin,EB Wolansky.Derivation and Experimental Verification of Design Formulae for Barrel-Shaped Helical Springs [J].SPRINGS,Winter 199736(1)：50-64.

[2]Keiji Hasegawa,Shinsuke Okura,Toshiyuki Imaizumi.New Technology of Manufacturing for Coil Springs Used in Automotive Suspensions [J].SAE Technical paper series N0.2002-01-0318.

[3]Varady T.,Martin R.R.,COXT J.Reverse engineering of geometric models：an introduction [J].Computer Aided Design, 1997,29(4)：253-330.

[4]柳江,莊德軍,喻凡,李明喜.基于點云數據的S型螺旋彈簧逆向設計[J].汽車技術,2006,(1)：17-18,45.