新型折疊裝置的優化仿真

張卓輝，李愛軍，郝國丹

ZHANG Zhuo-hui, LI Ai-jun, HAO Guo-dan

（中國礦業大學 機電工程學院，徐州 221116）

0 引言

現代服務產業是我國重點支持發展的產業之一，全自動折疊機將床單、被罩等酒店布草自動進行3-5折折疊，大量節省人力，其核心技術為傳動帶導向布草，利用吹氣、翻板和折刀進行折疊動作。作者研發了一種新型折疊裝置，對其進行了虛擬樣機的仿真分析，實現了敏捷制造。

圖1 折疊裝置結構圖

本折疊裝置工作原理如圖1所示，首先由氣缸3推動桿2，桿2則帶動刀板1擺動，并通過連桿5帶動連爪桿6和導布抓7一起擺動，從而實現布草在水平方向上中間對折。圖中箭頭方向為布草運動方向。

在現代大型洗滌服務行業，折疊機可以代替人工勞動，大大減輕工人的勞動強度，從而提高生產效率。折疊裝置的機構優化設計與運動仿真可以提高設計效率和設計質量，縮短設計周期。基于此，本文將機構的優化設計和運動仿真結合運用，對折疊裝置的結構進行優化，并用虛擬樣機技術仿真驗證優化結果。與優化前相比，簡化了彈簧機構為連桿機構，簡化了制造工藝。

1 優化設計

1.1 定義設計變量

首先用圖2所示的機構運動簡圖表示圖1所示的折疊裝置，其四個鉸點分別為A、B、C、D，AB、BC、CD和DA的長度分別為l1，l2，l3和l4。其中DA為機架，其長度l4是恒定的。機構起始角根據實際工作角度擬定，分別用θ3和θ1表示。因此，變量可簡化為三個，即l1，l2和l3，為三維優化問題，設計變量定義為：

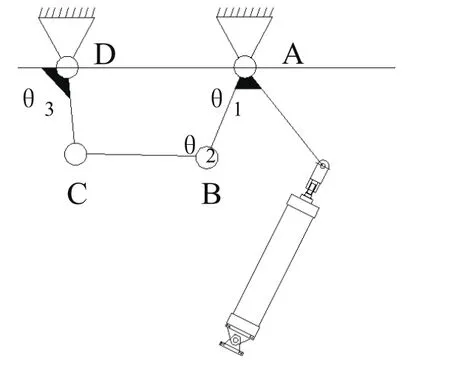
圖2 機構運動簡圖

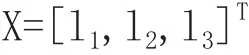
1.2 建立目標函數

為優化裝置結構，以桿件受力最小和桿件質量最小為目標，建立多個目標函數：

1）桿件所受力最小

其中，FAFBFCFD為ABCD四個鉸鏈處所受力。

2）桿件質量最小

由于各桿的材料相同，且橫截面積相差無幾，所以，要使桿質量盡可能小，應使桿長度盡可能小。

1.3 規定約束條件

考慮機構的動力學特性和結構要求，為使機構具備良好的傳力性能，應滿足：

根據折疊裝置的實際工作情況，DC桿的擺角為42.01°，如圖3的位置分析。

圖4 建模裝配

1.4 目標函數的簡化

由于優化目標多且計算量大，利用計算機強大的運算能力進行初步分析。用SolidWorks/COSMOSMotion軟件建立該折疊裝置的運動學模型，并對其進行仿真分析。

1.4.1 實體建模裝配

在SolidWorks中建立三維裝配模型，然后通過添加各種約束創建裝配體，如圖4所示。

1.4.2 COSMOSMotion仿真

由于該機構的自由度為1，故主動構件數只有一個，為AB桿1。利用step函數表達式模擬氣缸的運動，為桿1添加驅動，表達式為：

STEP(TIME,0,0,0.95,0)+ST EP(TIME,0.95,0,1,30D)+STEP(TIME,1.95,0,2,-30D)

這里只模擬一個周期，因此仿真時間為2.0 s。

COSMOSMotion進行運動學仿真，A、B、C、D四個鉸點的力如圖5(a)(b)(c)(d)所示。從圖5的性能參數可以看出，最大力的鉸點始終為A點。仿真為下一步的優化設計奠定了理論基礎。

圖5 ABCD四個鉸點的受力圖

1.4.3 目標函數的確定

由(b)的分析可知，A點受力一直最大，1.2中的目標函數ABCD四點力盡可能小可以簡化為使A點力盡可能小。

本機構優化設計的數學模型為求X=[l1,l2,l3]T

使得：

1.5 模型求解

粒子群算法(PSO)是Kennedy和Eberhart于1995年提出的一種模仿生物覓食行為來尋找最優解的算法，它是從隨機點出發同時利用微粒速度與位置上的信息，逐次迭代、最終找到全局最優解的優化算法。由于粒子群算法具有極強的魯棒性和全局尋優能力，且收斂快，人為干涉少，所以本文采用粒子群算法進行求解。算法步驟如下。

1）初始化粒子群：給定群體規模m，隨機產生每個粒子的位置P[i]，初始化每個粒子的速度v[i]=0。

2）計算每個粒子所對應的目標矢量。

3）初始位置P[i]作為每個個體歷史最佳位置Pb[i]。

4）初始化迭代代數t=0。

5）篩選粒子群中的非劣解放入外部文檔A。

6）循環迭代次數小于等于最大迭代次數M。

由于為2個目標尋優，所以根據用戶對子目標的重視程度設定權重系數。計算公式如下：

其中，s1，s2是用戶設定的各個目標模型的權重系數，且：s1+s2=1

優化目標是尋找S(X)的最優解，用MATLAB編程，編寫粒子群算法程序，按表1的參數設置初始值，計算過程如圖6所示，得到了最優解X=[l1,l2,l3]T=[53,60,40]T。

表1 粒子群算法的參數設置

2 仿真驗證

圖6 F (X)的進化曲線

圖7 桿1與氣缸接頭處的力矩曲線

按1.5的優化結果設置參數，X=[53,60,40]T，進行仿真驗證。利用SolidWorks尺寸驅動特點，只需修改桿的長度或夾角，裝配體會自動更新，即可再次進行仿真。通過改變桿長，以獲得桿件所受力盡可能小和桿件質量盡可能小。在改變桿長時，與更改前的仿真結果作為對比，如果增加桿長得到的結果在改善，則繼續增大其值，否則減小其值。這樣，反復比較修改，就可以獲得令人滿意的結果。最終獲得以下幾組優化數據：(a) X=[53,60,40]T，(b) X=[53,40,65]T，(c)X=[54,60,39]T。以(a)組數據為例，圖7為桿1與氣缸接頭處的力矩曲線，該曲線為氣缸的選型提供了理論依據。

3 結論

按上述方法對折疊裝置進行優化和仿真分析后得到的桿長，在深圳現代后勤集團技術設備研發生產中心制造樣機，進行了工業試驗。試驗結果表明，該裝置制造工藝簡單，穩定性和可靠性較好，尤其是在折疊厚布有較大的優勢，折布效果理想。

1）將機構優化與仿真結合起來，為折疊機構設計提供了一種可視化設計新思路，為機構強度校核計算奠定理論基礎，也為系統的動態特性提供理論依據。

2）通過優化設計折疊機構，本方法可行有效，提高設計效率和設計質量，大大降低了成本，帶來了十分明顯的經濟效益。

3）由于鉸聯接的轉動副存在微小的間隙，此間隙會影響機構的平動性，使銷軸的受力更為復雜，希望建立銷軸的動力學模型。

[1]王洪欣.機械原理[M].南京：東南大學出版社,2008.

[2]孫光永,李光耀,鐘志華,等.基于序列響應面法的汽車結構耐撞性多目標粒子群優化設計[J].機械工程學報,2009,45(2)：224-230.

[3]沈世德.實用機構學[M].北京：中國紡織出版社,1997.

[4]SolidWorks公司. COSMOS高級教程[M].北京：機械工業出版社,2008.