型鋼混凝土—鋼筋混凝土結構地震反應時程分析
沈古成 司旭濤 蘇艷梅
0 引言
《型鋼混凝土組合結構技術規程》中,將型鋼混凝土組合結構(Steel Reinforced Concrete Composite Structure)定義為混凝土內配置軋制型鋼或焊接型鋼和鋼筋的結構,簡稱SRC結構。結合我國的國情,考慮到工程造價、施工工藝、施工周期等各個因素的影響,在結構中完全采用型鋼混凝土結構是不現實的,而只能在一些結構的關鍵部位使用。本文所要研究的型鋼混凝土—鋼筋混凝土組合結構是在SRC結構的基礎之上,在我國有廣泛的應用前景。
時程分析法[1]通過逐步積分進行結構彈塑性動力分析,可以計算出地震反應全過程中各個時刻的內力和變形狀態,確定結構開裂和屈服的時刻和順序,發現應力和塑性變形集中的部位,從而判明結構的屈服機制、薄弱環節及可能的破壞類型。
1 動力方程
在對結構進行彈塑性反應分析時,因為剛度矩陣隨著時間而變化,振型頻率也隨時間而變化,因而振型分解法不宜在此使用,只能應用逐步積分法的直接動力法。要準確地研究結構或構件的彈塑性動力反應,需要解決的問題有很多,主要包括:地面運動、結構或構件的恢復力模型,計算模型的選取,動力方程的數值解法等。
一般多自由度體系的動力方程為:
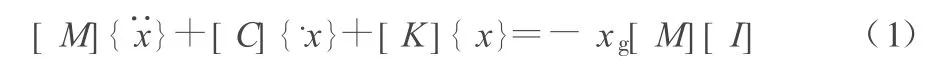
其中,[M]為質量矩陣;[C]為阻尼矩陣;[K]為剛度矩陣;xg為地面加速度;[I]為時間 t的函數;{},{x},{x}分別為結構的加速度、速度和位移反應列陣,均為時間t的函數。
當地面運動已知時,通過動力方程式(1)求解{x},{x},{x}采用逐步積分法。
多自由度體系在多維空間體系下的動力方程為:
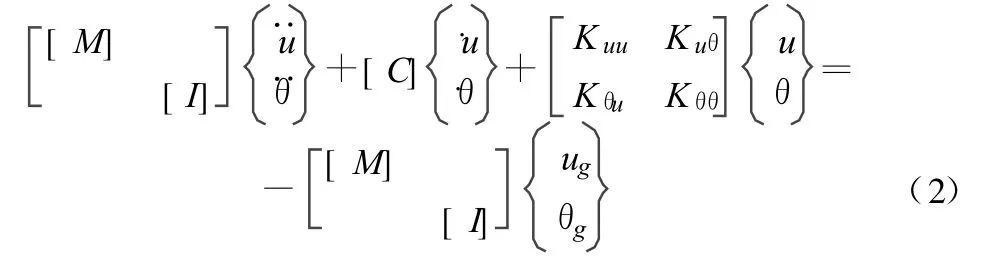
其中,[I]為截面慣性模量;{u},{u},{u},{θ},{θ},{θ}分別為結構平動的加速度、速度和位移反應列陣與轉動的加速度、速度和位移反應列陣[2]。
要將上式得出結果,需要確定結構的力學模型、恢復力模型、阻尼比和地震波等條件,還需一個良好的數值積分方法。
2 算例模型
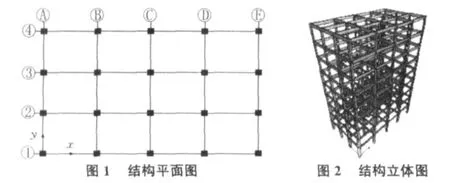
本例中的計算模型為9層型鋼混凝土—鋼筋混凝土組合結構框架,首層層高3.6 m,其他層層高3 m,總高度是27.6 m,結構平面圖如圖1所示,結構立體圖如圖2所示,場地類別為Ⅱ類,場地土特征周期為0.45 s,抗震設防烈度為7度,屬丙類建筑,抗震等級為三級,設地震分組為第一組,設計基本加速度值為0.1g。采用全框架結構體系,樓面采用150 mm厚混凝土板,板采用殼單元模擬,框架梁的尺寸為500 mm×250 mm,框架柱的尺寸及柱中型鋼尺寸如表1所示,梁、柱采用HRB335級鋼筋,柱的混凝土強度等級C30,梁的混凝土強度等級C20,樓面恒載取4.0 kN/m2,活載取2.0 kN/m2;屋面恒載取4.5 kN/m2,活載取0.5 kN/m2[3,4]。文中的方案一為純框架結構,方案二、方案三為型鋼混凝土與普通鋼筋混凝土的組合結構。
按照抗震規范,地震波選用EL-Centro波,其記錄峰值加速度為341.7 gal,卓越周期為0.55 s,時間步長為0.02 s,持續時間為30 s,按照7度基本烈度加速度時程曲線最大值要求,將地震波的峰值加速度放大值100 gal,在ETABS中輸入放大系數1 000/341.7=2.926 5。在基本烈度下的非線性彈塑性時程分析時,根據抗震規范,框架結構在多遇地震下的阻尼比,對超過 12層的可采用0.02;在罕遇地震下的分析,阻尼比可采用0.05。
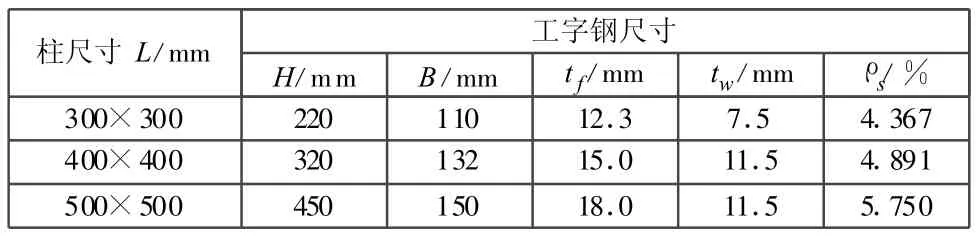
表1 型鋼尺寸表
3 計算結果
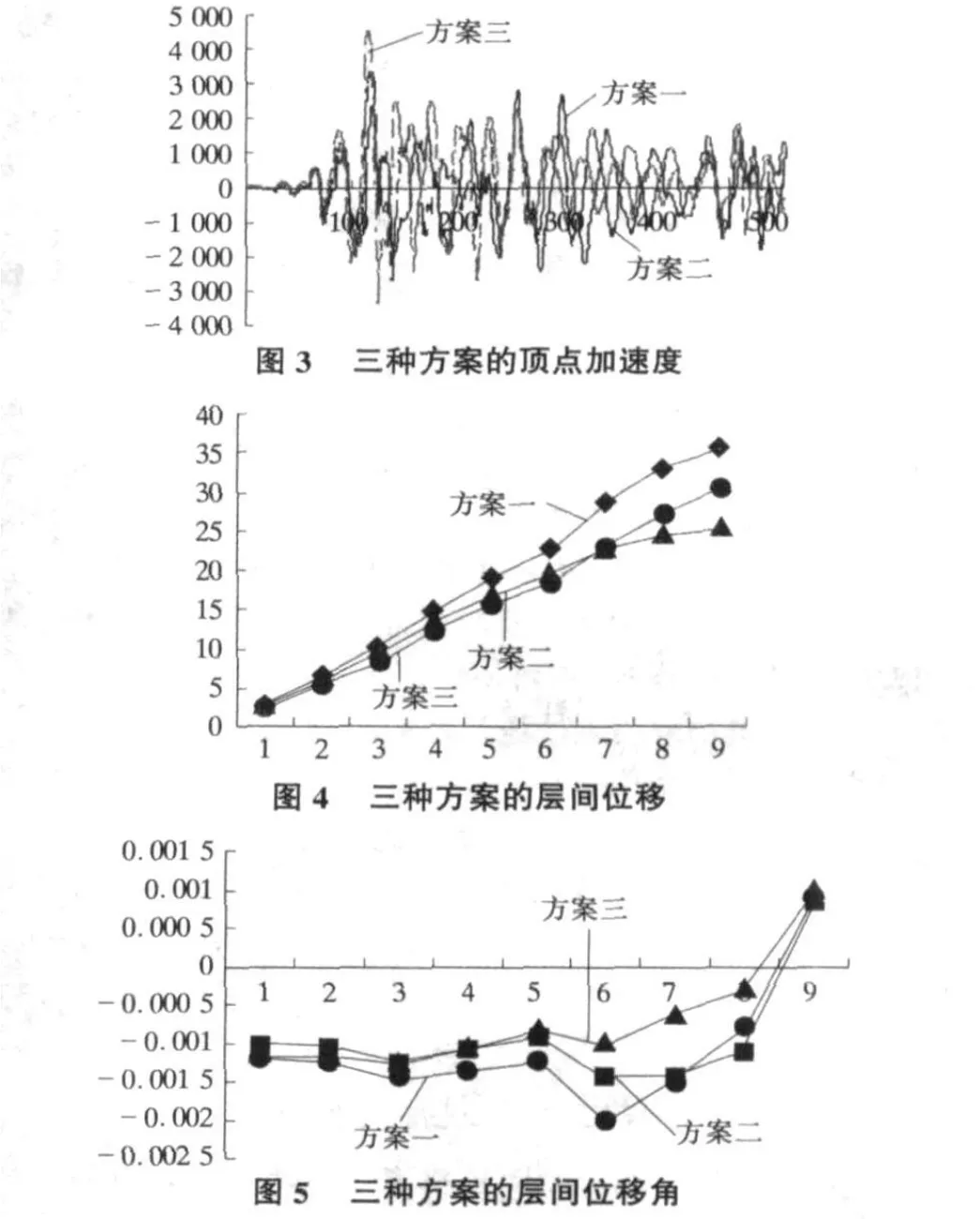
各種結構的頂點加速度、層間位移及層間位移角分別如圖3~圖5所示。
4 結語
從三種方案的頂點加速度曲線可以看出,型鋼混凝土的消能減震效果明顯;當然它們的層間位移角都小于1/50,符合規范要求。在EL-Centro波作用下,型鋼混凝土組合結構的最大位移比純框架結構的要小,其耗能性能比混凝土框架結構要好,故而應該推廣使用型鋼混凝土組合結構。
[1]蔣麗忠,王 臣.型鋼混凝土—鋼筋混凝土組合框架結構的地震彈塑性時程分析[J].鐵道科學與工程學報,2008,5(2):18-24.
[2]包世華,方鄂華.高層建筑結構設計[M].第 2版.北京:清華大學出版社,2000.
[3]GB 50009-2001,建筑結構荷載規范[S].
[4]陳基發,沙志國.建筑結構荷載設計手冊(第二冊)[M].北京:中國建筑工業出版社,2004.
[5]呂西林.高層建筑結構[M].武漢:武漢工業大學出版社,2000.
[6]齊 欣.型鋼混凝土—鋼筋混凝土混合框架抗震性能分析[D].成都:西南交通大學,2003.
[7]JGJ 138-2001,型鋼混凝土組合結構技術規程[S].

