基于Excel的 水力學隱式方程求解與輔助繪圖

鮑新華，盧文喜，李鴻雁，才文韜，譚劍鋒

（吉林大學環境與資源學院，吉林 長春 130026）

在管路水力計算、明渠臨界水深與均勻流水深計算、河道水面曲線計算、水躍共扼水深與水力消能計算、堰流計算以及某些經驗公式（如沿程阻力系數）等水力計算中，經常遇到求解隱式方程問題。試算法（含輔助圖解法）、標準曲線圖解法是常用的一類傳統方法[1～3]。這些傳統方法雖有優點，但不足也是明顯的。如試算法雖可以充分發揮計算者的經驗判斷，有時能給出比較接近結果的初值并較快得到結果，但由于求解常需要反復試算，有時配合輔助圖解法還存在讀數的精度誤差。

Excel作為Office常用組件之一，在工程與管理行業的統計、計算方面得到了全面的應用，但在水力計算中用于求解隱式方程還不多見[4，5]。由于Excel的數據運算能力、圖表功能和內含的單變量求解功能，將其引入水力學中求解隱式方程，與傳統方法相比具有求解簡單方便，通用性強的特點。

選用幾個水力學隱式方程典型算例，應用Excel單變量求解、迭代求解和輔助做圖功能，說明Excel用于水力學計算的簡單與方便。

1 Excel單變量求解

1.1 均勻流水深h或底寬b求解

例1：數據選自文獻[1]例5.3。已知等腰梯形斷面渠道設計流量Q，底坡i，底寬b，邊坡系數m和粗糙系數n，求均勻流水深h0。

從明渠均勻流基本公式入手，謝才系數采用曼寧公式，可以給出這種情況下的流量公式：

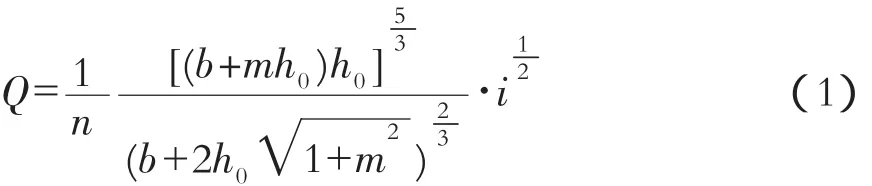
Excel單變量求解這一隱式方程基本過程為：在Excel工作表中A1∶F1單元格中輸入變量符號（僅作為標識，不參與運算），A2單元格中輸入上面的公式（注意公式以等號開始），B2∶E2輸入相應已知數值。當光標在任意單元格時，從“工具—單變量求解”出現的對話框中選擇輸入“目標單元格”和“可變單元格”絕對地址，然后輸入流量Q的目標值70后，見圖1。按確定則有求解結果為（圖 2）

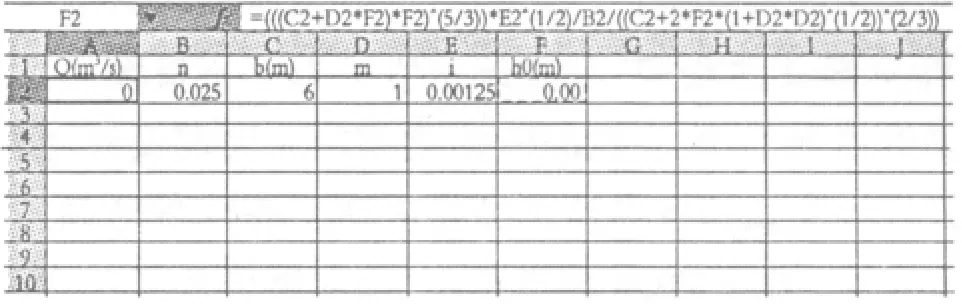
圖1 單變量求解均勻流水深過程

結果與文獻[1]基本相同，但由于試算法的近似和輔助做圖讀數的誤差，Excel單變量求解的精度顯然要高些。

圖2 單變量求解均勻流水深結果

1.2 非均勻流臨界水深hk求解

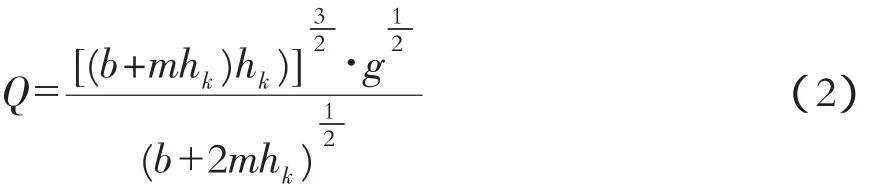
例2：數據選自文獻[1]例6.3。采用上面類似的方法，Excel單變量求解上述隱式方程的臨界水深 hk為 2.25 m（見圖 3）。

圖3 單變量求解等腰梯形斷面臨界水深hk

需要說明的是，求解前上述C2∶E2單元格的公式是按照公式（2）輸入的。

從上面2例可以看出，與試算法（含輔助圖解法）和標準曲線圖解法相比，Excel單變量求解水力學隱式方程，可體現出2個優點：①求解過程簡單，結果精度高。由于試算法需要多次反復試算，求解工作量較大。在不能大量試算的情況下，結果精度必然要受影響。試算的輔助圖解法和標準曲線（需有標準曲線模板）圖解，則有讀數誤差的影響。②對同一隱式方程，Excel單變量求解的工作表可以作為模板使用。參數不同，求解過程相同。由于隱式方程（如公式（1）或（2））是不變的，因此稍顯麻煩的公式僅需輸入一次，保留后就可以作為模板下次使用，使用時僅需要改變另一同類問題參數的數值再求解就可以了。特別是對同一隱式方程不同求解問題，只要使用的隱式方程不變，求解過程也是不變的。如在公式（1）中，在均勻流水深h和其它參數已知時求解底寬b，需要變化的只是可變單元格由h對應格變為b對應格而已（如例1中，可變單元格由F2變為B2），而這點變化對于求解并不增加任何工作量。

2 Excel迭代法求解

迭代法也稱輾轉法，是一種不斷用變量的舊值遞推新值的過程，也是隱式方程的另一種解法。這里我們主要采用簡單迭代法[6]。簡單迭代法在教材中均有少量介紹[1～3]，由于求解多采用計數器或編程法進行，一定程度上限制了迭代法的應用。而將Excel工具引入水力學隱式方程迭代求解具有簡單方便的特點。

水力學隱式方程采用迭代解法，首先應該根據隱式方程或方程的變形來確定迭代關系。隱式方程適當的變形可以有效減少迭代次數。其次是迭代初值的選擇，好的初值依靠經驗，不適當的初值可能導致不收斂情況的出現。再次是確定迭代結束的條件，通常可以迭代相對誤差來控制。考慮到初值常以0值開始和一次迭代有時就可能滿足精度要求的特例，取δ=更不失一般性。當迭代相對誤差很小時，比如小于1%，則可以結束迭代。

2.1 均勻流水深h或底寬b求解

例3：仍以上面例1數據為例，迭代求解等腰梯形均勻流水深h0。

對公式（1）變形有：

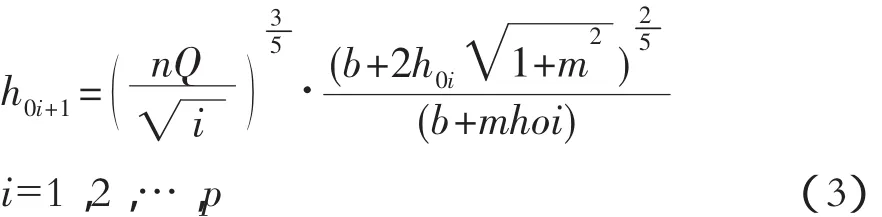
采用Excel進行迭代計算如下：

打開Excel表，輸入表頭標識，即將已知參數Qi，b，m，n，h0i，h0i+1，相對誤差 δ輸入到單元格內，然后把已知參數值輸入到下一行相應位置。在G2單元格（h0i+1單元格）內輸入下列公式（即公式（3），注意單元格地址的絕對和相對引用）=($E$2*$A$2/($B$2^(1/2)))^(3/5)*(($C$2+2*F2*((1+$D$2*$D$2)^(1/2)))^(2/5))/($C$2+$D$2*F2)

取h0i=0為初值，在F2單元格內輸入初值0，在F3單元格內輸入=G2,，在H2單元格內輸入=ABS(G2-F2)/G2?100，然后拖動填充柄對單元格G3和H2分別向下復制公式，公式復制的過程實際上就是Excel的迭代過程！迭代終止以相對誤差小于1%作為結束標志，最終結果取滿足要求時h0i+1單元格中的數值。從圖4可以看出，本例僅迭代2次就達到了給定的精度要求，結果與前面單變量求解結果是一致的（見圖2，4）。

圖4 迭代法求解均勻流水深結果

在例1中，如果已知等腰梯形斷面渠道設計流量Q，底坡i，均勻流水深h0，邊坡系數m和粗糙系數n，求底寬b。則可以對式（3）變形有：

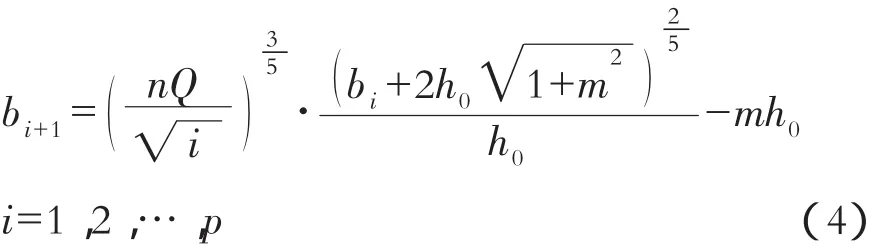
迭代求解方法與例3類似，此略。

2.2 沿程阻力系數λ求解

例4：例題取自文獻[3]，已知雷諾數Re=48 595，水流型態處于紊流光滑區，要求采用尼古拉茲光滑管公式計算沿程阻力系數λ。

尼古拉茲光滑管公式變形為迭代形式為

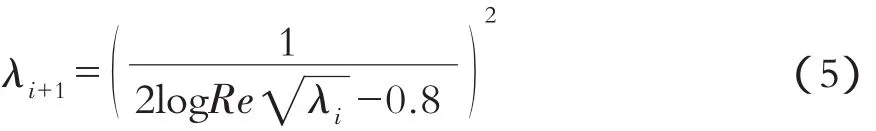
Excel迭代運算表見圖5。取不同非零初值（對數函數自變量不能取零值），不同迭代初值對應結果見表1。

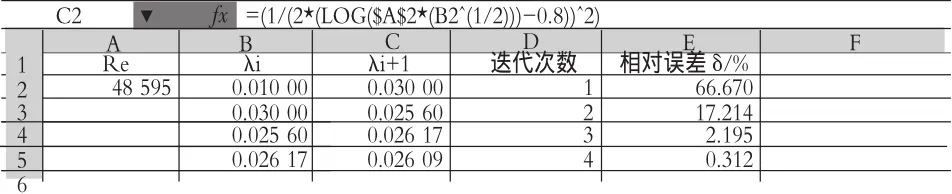
圖5 迭代法求解沿程阻力系數λ

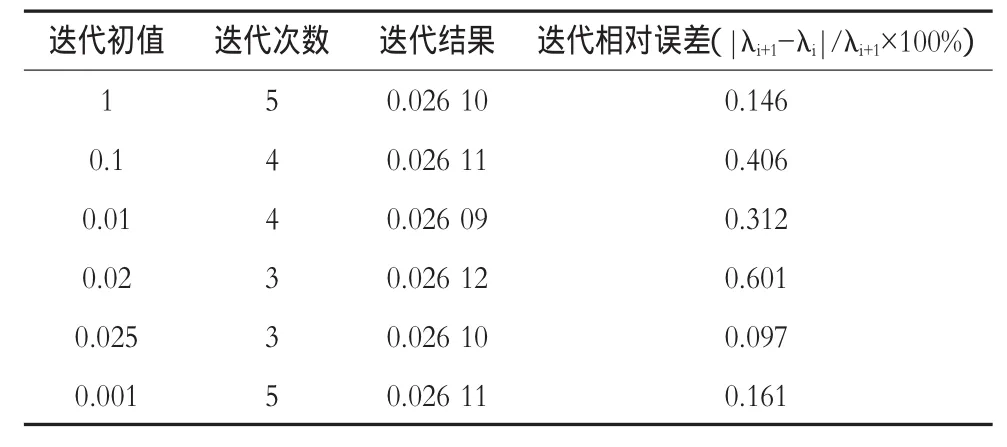
表1 沿程阻力系數λ迭代結果比較

從某種意義上看，水力學隱式方程的迭代解法類似有序的試算法，是從一個初始值出發，不斷逼近精確解的過程。求解前一般先把方程變形為x=f(x)的形式（如公式（3～5）），采用 xi+1=f(xi)迭代式，采用簡單迭代法來求解。通過筆者教學中對多數水力學隱式方程計算表明，一般簡單迭代法多能收斂并得到滿足精度的結果。

此外，觀察表1，還應注意到迭代相對誤差與結果的誤差是有所區別的。例4中取λ=0.026 10作為結果精確值的話，表中有二個相同的結果與此一致（不考慮舍入誤差），但它們的迭代相對誤差是有區別的，而作為最終結果，其誤差應該是一致的。但這種迭代相對誤差與結果的誤差在應用中基本可以忽略。

從上面的例題看，由于Excel強大的表格運算功能，不用編程就可以利用Excel方便完成迭代過程，這表明使用Excel迭代解法求解水力學隱式方程具有簡單方便的特點。需要說明的是，除了簡單迭代解法外，牛頓迭代等迭代解法也是可以應用的，限于篇幅，這里就不介紹了。

3 Excel求解與繪圖

利用Excel不僅可以對隱式方程進行單變量法和迭代法求解，還可以利用Excel強大的圖表功能，對相關問題進行輔助制圖，下面舉例說明這方面的應用。

例5：例題取自文獻[1]例6.6，對長直棱柱狀明渠，已知底寬b、邊坡系數m、粗糙系數n、流量Q、末端水深h，求明渠均勻流水深h0、臨界水深hk，并繪制水面曲線。

首先，選用Excel單變量求解法，求解本問題的均勻流水深h0、臨界水深hk見圖6，并作為進一步分析的初始數據。

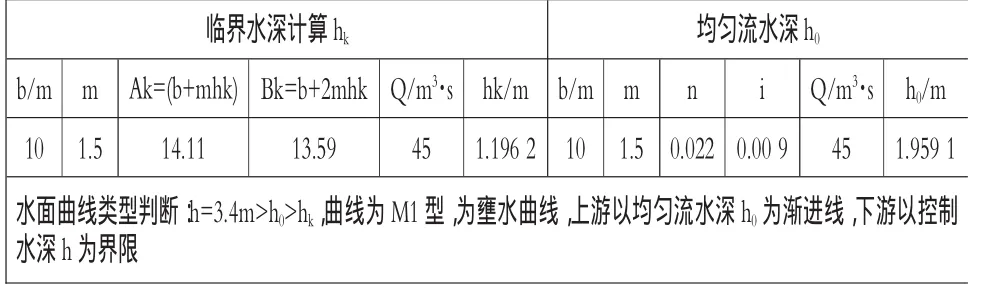
圖6 Excel單變量求解均勻流水深h0、臨界水深hk

然后利用文獻[1]相關公式，用Excel分流段列表計算水深，計算表見圖7。

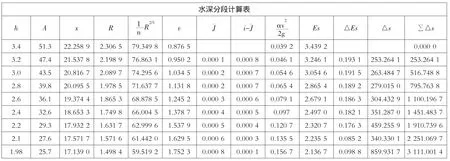
圖7 Excel水深分段計算表

為利用Excel繪圖，利用圖6，7數據，形成一個Excel輔助表（見圖8），然后根據輔助表，利用Excel繪圖功能繪制的水面曲線見圖9。

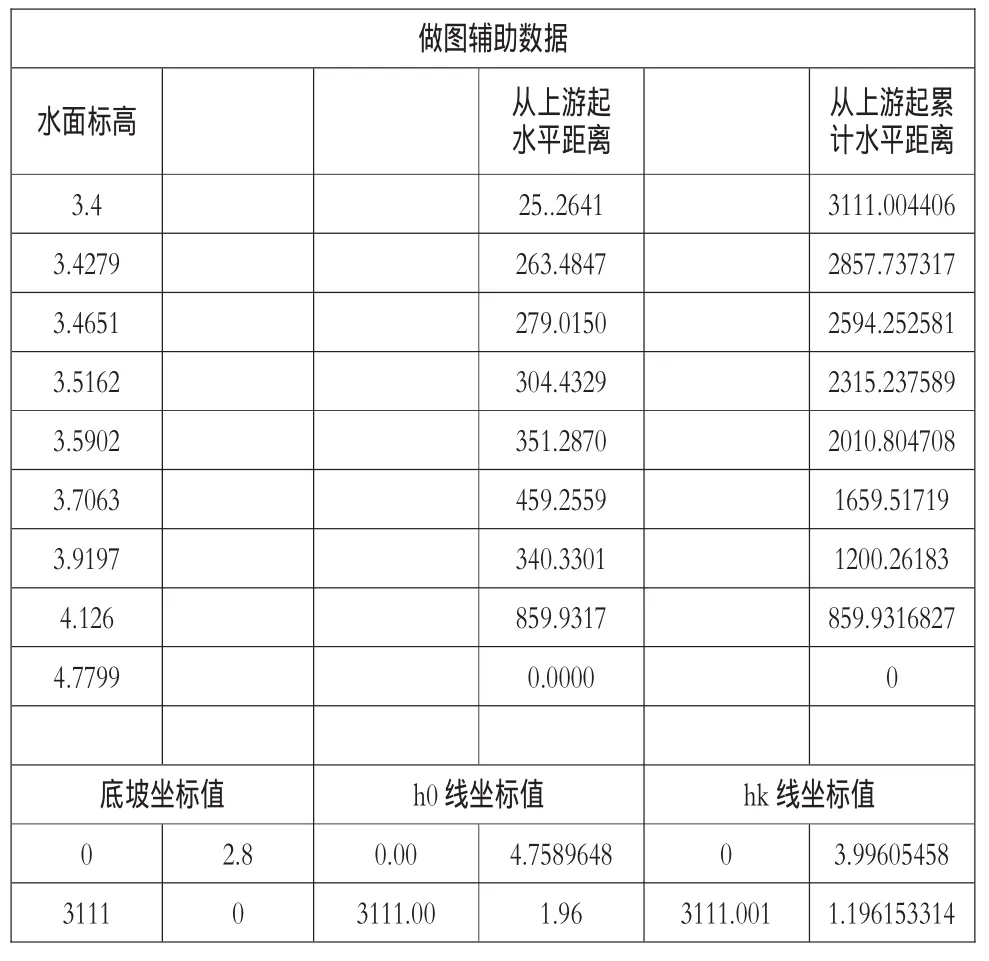
圖8 Excel輔助繪圖數據表

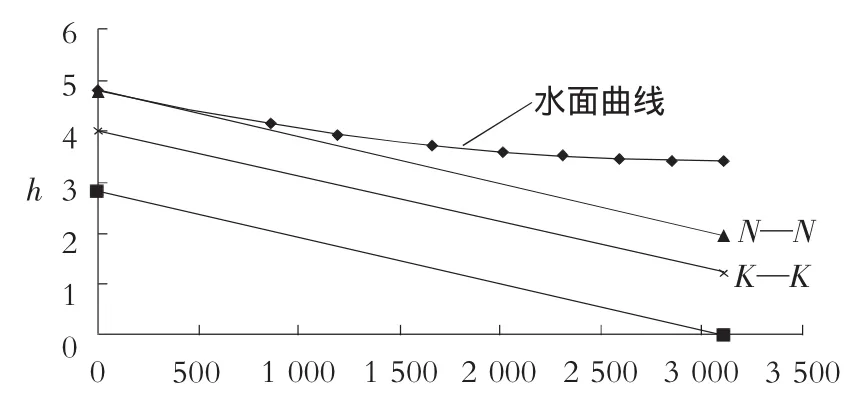
圖9 Excel繪制的水面曲線

雖然本例中一些具體細節限于篇幅這里沒介紹，但對Excel稍有熟悉的讀者是不難從上面介紹中掌握這一簡單方法的。雖然這里介紹的利用Eecel輔助繪圖只是一個簡單例子，但由于Excel的基于數據表的強大繪圖功能，對水力學中許多數據圖，甚至標準曲線等都是可以應用的。

4 結論

從上面幾個實例介紹可以看出，Excel的單變量求解法和簡單迭代法應用于求解水力學單解隱次方程具有簡單方便、精度高和通用性強的特點，可以作為水力學試算法（含輔助圖解法）、標準曲線圖解法之外的另一種求解方法。將Excel強大的數據處理和繪圖功能應用于水力計算中具有簡明方便的特點，可以發揮一定的積極作用。

作為已廣泛使用的Office辦公軟件組件之一的Excel工具的使用，在水力計算中，無論是現行教材還是應用文獻看，都還不多見。作為一種方便成熟的工具，本文呼吁將Excel應用引入教材，并在實際計算應用中加以積極推廣。

[1]吳持恭.水力學[M]，第4版.北京：高等教育出版社，2008.

[2]趙振興，何建京.水力學[M].北京：清華大學出版社，2005.

[3]李大美，楊小亭.水力學[M].武漢：武漢大學出版社，2004.

[4]張 錦.Excel在水力計算中的應用探討[J].甘肅水利水電技術，2002，38（4）：301-302.

[5]鄒 健.雍水曲線的新式解法.西部探礦工程[J]，2006，8：216-217.

[6]李有法，李曉勤.數值計算方法[M]，第2版.北京：高等教育出版社，2005.

[7]Excel規劃求解水—巖作用模型[J].地下空間與工程學報，2008，4（2）：265-268.