噪聲環境下畸變模型線性化處理的頑健語音識別方法

何勇軍，韓紀慶

(1. 哈爾濱工業大學 計算機科學與技術學院，黑龍江 哈爾濱 150001；2. 哈爾濱理工大學 計算機科學與技術學院，黑龍江 哈爾濱 150080)

1 引言

在語音識別中，加性噪聲和信道畸變一直是導致系統性能下降的重要原因。數 10年來，在提高語音識別系統環境頑健性方面，研究者們做了大量工作，取得了一定進展。目前存在的方法大致可分為特征增強和模型補償/適應2大類[1]。前者提取頑健性特征來提高系統性能；后者則訓練適應噪聲環境的聲學模型來降低環境失配的影響。在現實環境中，語音通常同時受加性噪聲和信道畸變的影響，同時補償這2類畸變對于增強語音識別系統頑健性具有重要意義。聯合補償方法(JAC, joint compen-sation of additive and convolutive distortions)[2～4]試圖達到這一目標。它在期望最大化(EM, expectation-maximum)框架下估計噪聲參數然后補償模型參數，能有效提升語音識別系統的識別率，其性能明顯優于特征增強類方法。更重要的是，JAC類方法在識別過程中進行補償，無需額外的標注數據。在補償過程中，JAC類方法需要噪聲參數的顯式表示，但以MFCC為特征的系統，畸變語音和干凈語音以及噪聲之間的關系式呈高度非線性[2]，其中噪聲參數無法被解析表達，這導致參數估計難以準確實現。

JAC用一階VTS將非線性畸變模型展開[2～6]，獲得噪聲參數的近似解析表達式。由于一階 VTS存在較大誤差，這使得JAC類補償方法對系統性能的提升受到限制。通過研究發現，計算MFCC過程中的對數運算將導致語音和噪聲參數呈非線性。針對這一點，本文將對數運算用其分段線性插值函數代替，構建新的線性畸變模型，并在此基礎上導出了噪聲參數估計和模型補償公式。與現有JAC類方法相比，本文方法建立在線性畸變模型之上，避免了使用一階 VTS展開所引入的模型誤差。實驗表明，該方法能有效提高系統識別率。

2 對數函數的分段線性插值近似

一階 VTS用過展開點的切平面近似代替真實模型的曲面，當展開點附近的真實曲面曲率較大或選擇的展開點距離觀察值較遠時，線性化后的畸變模型將存在較大誤差；另一方面，展開點的選擇目前尚無規律可循，也是一個有待解決的問題。二階及其以上VTS計算復雜度將急劇增加，而且也無法獲得噪聲參數的解析表達式，難以用于模型補償。對數運算能將乘積運算轉化為加運算，但在加性噪聲存在時卻使得畸變模型呈高度非線性。因此，提出用分段線性函數對對數函數插值近似，建立線性畸變模型。

MFCC的計算是先對信號分幀，作離散傅立葉變換(DFT, discrete Fourier transform)，然后加梅爾濾波器組并對其輸出取對數，最后作離散余弦變換(DCT, discrete cosine transform)，如圖1的虛線。本文特征按照圖1實線的方向計算。在實驗中，先統計梅爾濾波器輸出的上限D1和下限D2，然后在[D1,D2]內計算對數函數的分段線性插值函數即可滿足系統需求。

圖1 本文特征與MFCC特征的計算對比

假定在區間[D1, D2]上存在等比排列的點：D1=d0, d1,…, dp=D2，即 dr=qdr-1, r=1, 2,…, p，其中，q取大于1的常數，p為區間個數。在區間[dr,dr+1]上，用過點(dr, ln(dr))和(dr+1, ln(dr+1))的線段代替對數曲線，其中，ln(·)代表自然對數運算。由于自然對數的變化率隨自變量增加而減小，在自變量較小的區間上需要較多的線段去逼近，因此，這里采用逐漸遞增的等比數列分割定義區間。

在任意一個區間[dr, dr+1]上，系數ar、br是完全確定的。對于一次運算，只要確定函數值lr(x)和自變量x中的任意一個即可確定運算系數。

在后面的運算中，需要對關系式 y=hx+n兩端進行運算，其中，x、y分別代表某一梅爾濾波器上干凈語音和混噪語音的輸出，h、n分別代表信道和加性噪聲參數。若x∈[ds, ds+1]，y∈[dr, dr+1], 其中，s, r=1, 2, …, p可以相同也可以不同，則有ls(x)=asx+bs且

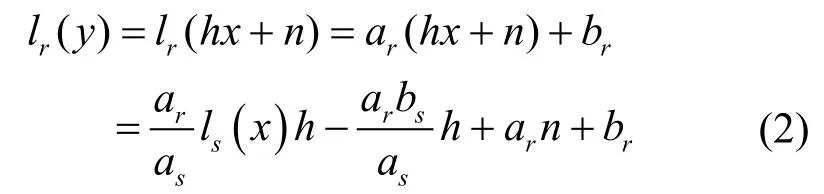
式(2)為干凈語音、畸變語音以及噪聲參數建立的線性關系。這樣表示既可實現干凈語音模型和畸變語音模型之間的相互轉換，又便于噪聲參數由其他參數表達。在噪聲參數 h、n確定時，已知 ls(x)可確定as、bs，然后用hx+n= h[(ls(x)-bs)/as]+n確定ar、br，即可求出lr(y)。反之，如已知lr(y)，也可確定ar、br，計算出y=hx+n，進而求出x并確定as、bs，最后求出ls(x)。

3 對數運算線性化情況下的畸變模型

在頻域畸變語音的功率譜可表示為[7]

其中，k=1, 2,…, K為DFT序號，X[k]和Y[k]分別為干凈語音和畸變語音的DFT，H[k]和N[k]分別為信道畸變和加性噪聲的DFT。等式兩端加梅爾濾波器組 ：，其中，l=1, 2,…, L，L為梅爾濾波器個數，表示第l個梅爾濾波器在第k個頻譜分量上的值，并令

則第l個梅爾濾波器的輸出為

在MFCC的計算過程中，接下來要作對數運算，這里用其分段線性插值函數代替。根據式(2)有

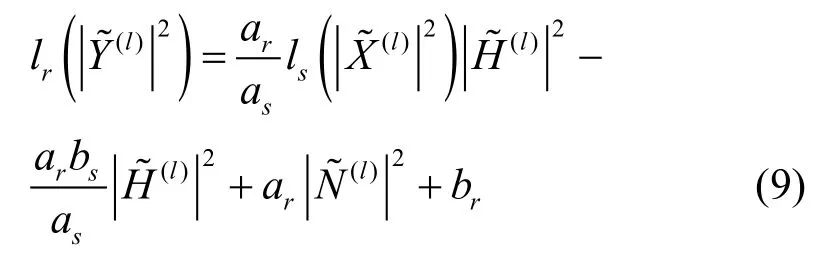
等式兩端作 DCT，并采用與文獻[2]類似的處理方式，令

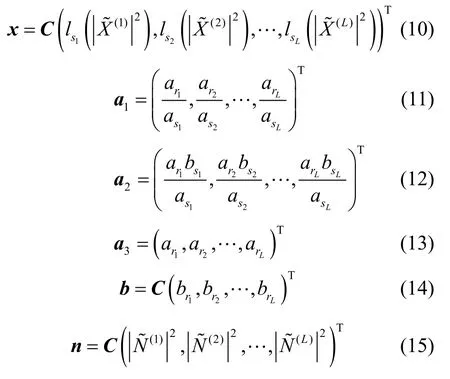
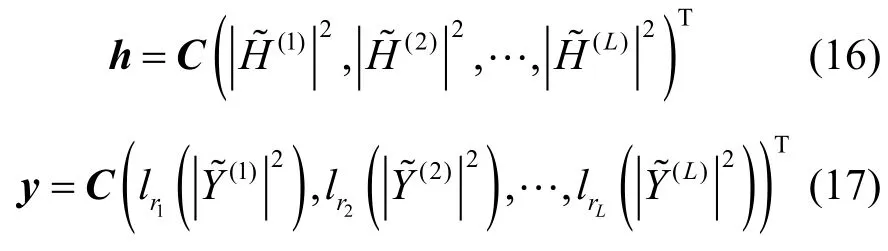
其中，C為DCT矩陣，T為轉秩運算。由于每個梅爾濾波器上的能量輸出值可能處于不同區間，在運算時要用到不同的分段函數，這里用下標rl和sl表示第l個梅爾濾波器上的輸出和所處的區間。其中，系數向量a1、a2及a3內對應元素按式(2)的系數確定方式確定。則畸變模型表示為

或

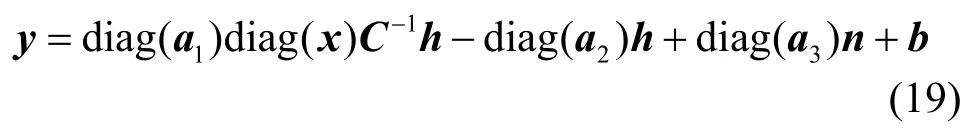
其中，diag(a)表示以向量a為主對角元素的對角陣。式(18)和式(19)為線性表達式，噪聲參數 h和 n均可被解析表達。在后面實驗中將看到，線性化對數運算之后計算的特征在干凈語音情況下，識別率不低于MFCC特征；在噪聲環境下，基于線性化模型的補償方法明顯優于一階VTS類JAC方法。

4 線性畸變模型下干凈模型參數與畸變模型參數的關系

目前大詞表連續語音識別系統普遍基于隱馬爾可夫模型(HMM, hidden Markov model)，其各個狀態用高斯混合密度函數建模。噪聲在模型上的影響表現為改變各高斯分量的均值和方差。假定加性噪聲在同一單句中服從未知均值和方差的高斯分布，信道畸變保持不變，二者在句子之間可以變化[3]。對式(18)兩端取均值：

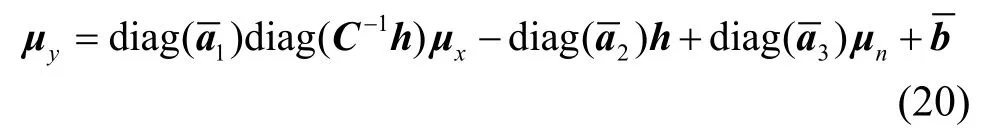
其中，μy、μx和μn分別為畸變語音、干凈語音以及加性噪聲的特征均值向量，系數向量、、和的確定方式同前。當給定噪聲參數h和μn，畸變語音聲學模型的第j個狀態的第k個高斯分量的均值只與干凈語音的聲學模型對應均值有關，即

其中，μx,jk和μy,jk分別為干凈語音和畸變語音模型的第j個狀態的第k個高斯分量的均值向量，同理對式(18)兩端求協方差有

其中，Σx,jk、Σy,jk和Σn分別為干凈語音、畸變語音以及加性噪聲的協方差。當計算差分的窗口較小時，用與文獻[4]類似的處理方法，聲學模型的動態參數更新如下：

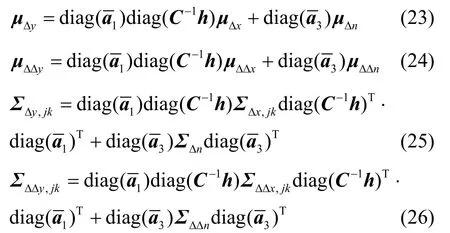
本文中Δ表示一階差分，ΔΔ表示二階差分。在確定噪聲參數時，通過干凈聲學模型參數用式(20)～式(26)計算畸變聲學模型參數，再用更新后的模型識別語音以解決環境失配問題。本文方法不僅考慮了模型均值的更新，也考慮了模型方差的更新。

5 噪聲參數的估計

噪聲參數包括信道參數h和加性噪聲均值參數μn、μΔn、μΔΔn及其方差參數 Σn、ΣΔn、ΣΔΔn。接下來將在EM框架下給出噪聲參數的估計方法。如果一句發音的MFCC靜態特征為Y={y1, y2,…, yN}，其中，N為特征向量個數，構建Q函數[4]：

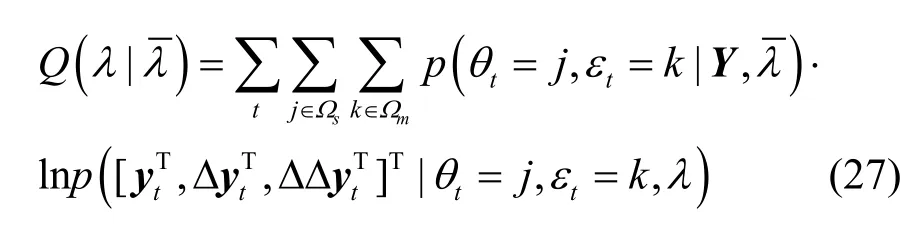
由于各噪聲參數在新的畸變模型下可顯式表示，本文采用與文獻[3]類似的策略，即先優化畸變模型，然后用畸變模型表達式優化噪聲參數。Q函數對均值求導后令其等于 0，并按所有 j、k進行疊加，同時考慮到各維特征系數不相關，有代入式(21)解出信道參數：

EM 算法通過迭代使估計量收斂于其極大似然估計值，設第 i次迭代時加性噪聲均值為，則據上式第i+1次迭代得到的信道參數為

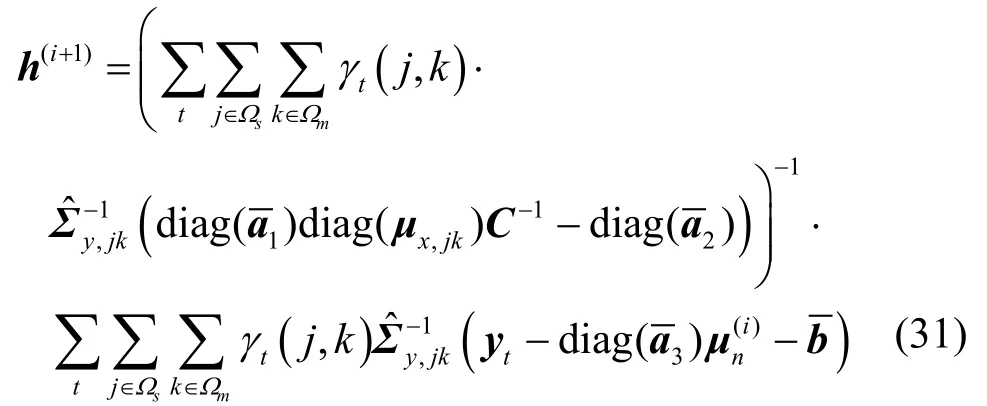
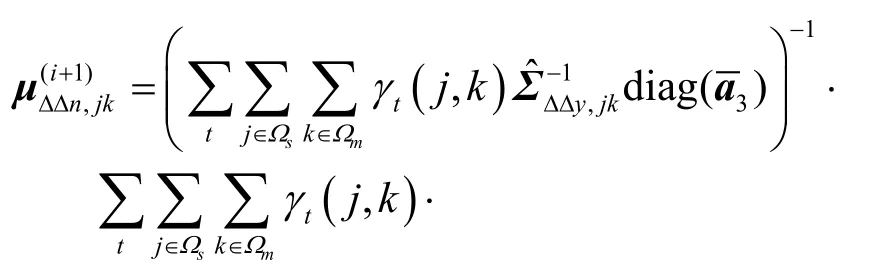
代入式(22)解出nΣ并構建迭代公式為

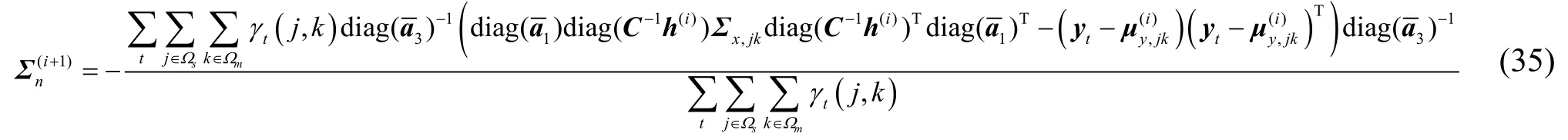
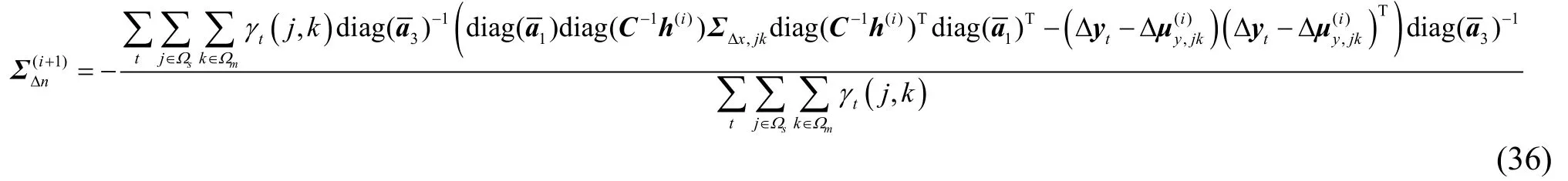
用本文的線性畸變模型估計出需要的噪聲參數，再用第三部分的模型更新公式更新聲學模型，反復迭代，使聲學模型與噪聲環境匹配。

6 識別過程

識別時以句子為單位估計噪聲參數并更新聲學模型，再用更新后的模型識別該句子。現將識別過程以偽代碼形式敘述如下。

for每句語音S

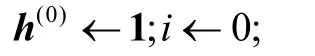
用 S的 前 N 幀非語音幀初始化 n(0)和 Σ(0);

whilei ＜ I

用前次迭代更新后的模型識別S;

計算 γt( j , k )(式 (29));

計算 h(i+1)(式 (31));

i ← i +1;

e nd while

用最后的模型識別句子S;

end for

其中，I為最大迭代次數，每次更新模型參數時都采用最新估計的噪聲參數。為標記方便，符號下標jk被略去。由于信道參數未參與對數運算，其初始值為全1向量，這有別于基于MFCC特征時的初始化。

7 實驗結果與分析

實驗使用King-ASR-009語料庫[8]，該語料庫含有200名(87男，113女)不同年齡、發音、文化層次的發音人。使用 4種通道(SHURE SM58、ANC-700、TELEX M-60和ACOUSTIC MAGIC，分別記為Mic1、Mic2、Mic3和Mic4)同時錄音，錄制每人朗讀的 120條短信文字。數據采樣率22.05kHz，量化16bit。本文將所有數據重新采樣，使其采樣頻率為16 kHz。

實驗選取Mic1下100人(50男，50女)的12 000句(每人120句)語音訓練聲學模型。Mic1數據質量較好，被看作干凈語音，其他麥克風具有不同程度的信道畸變。用Mic1及其他信道下另外40人(20男，20女)的語音，以一定的信噪比疊加噪聲，形成噪聲環境下的測試語音。實驗使用Noise-92噪聲庫的4種噪聲，即White、Factory、Babble和Leopard，每種噪聲以一定的信噪比 (SNR, signal to noise ratio) 疊加在干凈語音上。在數據選擇上，訓練集和測試集說話人沒有重疊，配置情況見表1。

表1 訓練集和測試集配置情況

實驗采用劍橋大學的 HTK工具。前端處理的預加重系數為0.97，梅爾濾波器組的濾波器個數為33，短時傅立葉變換點數為512，幀長為30ms，幀移10ms。本文方法選取13維特征系數及其一階、二階差分構成 39維特征向量；基線系統及其他用于比較的方法采用相同設置的MFCC特征。系統訓練3音子綁定聲學模型，詞典中將每個漢字分解成音素，并用863中文語料庫和King-ASR-009中所有文本訓練三元統計語言模型。選擇[0.001,100]為對數函數插值區間。目前語音識別系統常用的基于一階VTS的JAC方法[4](記為VTS)、倒譜均值規正(CMN, cepstral mean normalization)[9]、相關譜濾波(RASTA, relative spectra)[10]、譜減(SS, spectral subtraction)[11,12]和模型自適應(最大似然線性回歸[13]和最大后驗概率[14])被用于對比實驗。從每個測試集中選擇每個人的前5句發音作為對應環境的自適應數據。自適應時，先進行最大似然線性回歸自適應，然后作最大后驗概率自適應。

首先在無噪情況下測試了MFCC特征與本文特征在劃分區間數p取不同值時(記為MFC-p)的識別率。在實驗中選用測試集0為測試數據，實驗結果見表2。

表2 MFCC與MFC-p識別率對比

本文統計的是漢字識別率。從實驗結果可以看出，在無噪情況下，MFCC特征識別率為87.2%。使用本文特征，當p小于5時，識別率僅有少量下降，而當p大于等于5時，識別率回到MFCC特征的水平。隨著p的繼續增加，識別率保持不變。考慮到計算速度，在后面的實驗中，本文方法一律使用MFC-5，參數估計時最大迭代次數為6。

然后采用測試集 1測試各方法在信道畸變下的性能，即用Mic1數據訓練的模型識別Mic2～Mic4下的數據，實驗結果見表3。不作任何補償的基線系統性能較差，最好的情況不超過 50%。CMN和RASTA聯合使用對信道畸變有一定效果，識別率有較大提高；VTS和模型自適應取得了更好的性能。相比之下，本文方法能進一步提高系統識別率，在3個通道上的識別率都在75%以上，性能優于VTS。

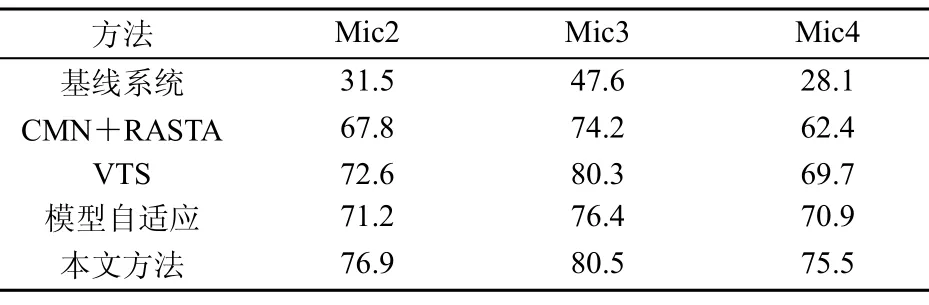
表3 信道畸變情況下各方法性能對比(識別率/%)

接下來用測試集2測試各方法在僅有加性噪聲存在時的性能，實驗結果如圖2所示。基線系統的性能隨著信噪比的降低而迅速降低，尤其是在SNR＝5dB高斯白噪聲情況下，識別率僅25.4%。CMN＋SS與VTS以及模型自適應方法較大幅度地提升了系統識別率。模型自適應方法在多數情況下優于CMN＋SS卻不及VTS。盡管可以預料，隨著自適應數據的增加，模型自適應性能會逐漸上升，但需要額外訓練語料不便于現實應用。VTS和本文方法均無需額外訓練數據，而本文方法對加性噪聲的補償效果更為明顯，在 SNR=5dB時使得系統識別率在70%左右，在SNR=25dB時，4種噪聲下的識別率分別為79.1%、81.9%、82.2%和82.6%。

圖2 加性噪聲情況下各方法性能對比

最后用測試集3測試各方法在加性噪聲和信道畸變同時存在時的性能，實驗結果如圖3所示。可以看出，基線系統在所有情況下，識別率都不超過40%。本文方法在SNR=25dB時的White和Factory噪聲下略高于 VTS，在其他情況下能比 VTS提升3～4個百分點。這進一步說明了本文方法的有效性。

圖3 加性噪聲和信道畸變同時存在時各方法性能對比

8 結束語

在 MFCC域含噪語音的畸變模型呈高度非線性，這使得模型域方法無法直接使用畸變模型估計噪聲參數。基于一階VTS的方法雖然能將畸變模型線性化，但其誤差限制了這類方法性能的進一步提升。本文針對該問題提出了一種新的線性畸變模型，并在此基礎上，導出了噪聲參數估計和聲學模型補償方法，最后用實驗驗證了其有效性。

[1] YUSUKE S, MASANMI A. Bayesian feature enhancement using a mixture of unscented transformations for uncertainty decoding of noisy speech[A]. Proceedings of ICASSP[C]. Taiwan, China, 2009.4569-4572.

[2] ACERO A, DENG L, KRISTJANSSON T, et al. HMM adaptation using vector Taylor series for noisy speech recognition[A]. Proceedings of ICSLP[C]. Beijing, China, 2000. 869-872.

[3] GONG Y F. A method of joint compensation of additive and convolutive distortions for speaker-independent speech recognition[J]. IEEE Transaction on Speech Audio Processing, 2005, 13(5)∶ 975-983.

[4] LI J Y, DENG L, YU D. A unified framework of HMM adaptation with joint compensation of additive and convolutive distortions[J].Computer Speech and Language, 2009, 23(3)∶ 389-405.

[5] VAN D, GALES M. Extended VTS for noise-robust speech recognition[A]. Proceedings of ICASSP[C]. Taiwan, China, 2009. 3829-3832.

[6] GALES M, FLEGO F. Combining VTS model compensation and support vector machines [A]. Proceedings of ICASSP[C]. Taiwan,China, 2009. 3821-3824.

[7] LIAO H, GALES M. Joint Uncertainty Decoding for Robust Large Vocabulary Speech Recognition[R]. Technical Report CUED/TR552.University of Cambridge, 2006.

[8] KING-ASR-009. A Chinese speech database for speech recognition[EB/OL].http∶//www.speechocean.com/productdetail.asp?id=Ki ng-ASR-009,2010.

[9] STEVEN F B, DENNIS C P. Feature and score normalization for speaker verification of cellular data[A]. Proceedings of ICASSP[C].Hong Kong, China, 2003. 49-52.

[10] HERMANSKY H, MORGAN N, BAYYA A. RASTA-PLP speech analysis technique[A]. Proceedings of ICASSP[C]. San Francisco,USA, 1992. 1121-1124.

[11] BOLL S, PULSIPHER D. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE Transaction on Speech Audio Processing, 1979, 27(2)∶ 113-120.

[12] MARTIN R. Noise power spectral density estimation based on optimal smoothing and minimum statistics[J]. IEEE Transaction on Speech Audio Processing, 2001, 9(5)∶ 504-512.

[13] SAON G, HUERTA H, JAN E E. Robust digit recognition in noisy environments∶ the IBM Aurora 2 system[A]. Proceedings of Interspeech[C]. Aix-en-Provence, France, 2001. 629-632.

[14] HUO Q, CHAN C, LEE C H. Bayesian adaptive learning of the parameters of hidden Markov model for speech recognition[J]. IEEE Transaction on Speech Audio Processing, 1995, 3(5)∶ 334-345.