基于ANSYS的磁懸浮軸承轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)特性研究

萬(wàn)金貴，汪希平，高 琪，張 飛

(1.上海第二工業(yè)大學(xué) 實(shí)驗(yàn)實(shí)訓(xùn)中心,上海 201209；2.上海大學(xué) 機(jī)電工程與自動(dòng)化學(xué)院，上海 200072)

主動(dòng)磁懸浮軸承(active magnetic bearing， AMB)是利用電磁鐵產(chǎn)生可控電磁力將轉(zhuǎn)子懸浮支承的一種新型軸承，由于具有一系列獨(dú)特的優(yōu)點(diǎn)而引起人們的廣泛關(guān)注[1]。近年來(lái)，AMB技術(shù)在國(guó)外得到了迅速的發(fā)展，已在軍工、航天等國(guó)防工業(yè)部門(mén)中得到了廣泛應(yīng)用，并向民用工業(yè)如航空、機(jī)床、化工、能源等領(lǐng)域推廣[2-4]。

主動(dòng)磁懸浮軸承經(jīng)常工作在每分鐘數(shù)萬(wàn)至數(shù)十萬(wàn)轉(zhuǎn)范圍內(nèi)，此時(shí)的轉(zhuǎn)子動(dòng)力學(xué)行為往往表現(xiàn)為柔性轉(zhuǎn)子的特性[5]。為保證磁懸浮轉(zhuǎn)子系統(tǒng)的安全穩(wěn)定運(yùn)行，設(shè)計(jì)者需要對(duì)系統(tǒng)的動(dòng)力特性進(jìn)行分析和計(jì)算，并可對(duì)磁力軸承動(dòng)力學(xué)行為進(jìn)行調(diào)整和控制[6-7]。由于磁力軸承的結(jié)構(gòu)涉及到由電子電路組成的控制器，因此其動(dòng)力學(xué)特征與傳統(tǒng)軸承有著本質(zhì)區(qū)別。目前，人們對(duì)于磁懸浮軸承轉(zhuǎn)子系統(tǒng)的動(dòng)力特性普遍規(guī)律還沒(méi)有形成成熟的理論。因此，分析磁懸浮轉(zhuǎn)子系統(tǒng)動(dòng)力特性，探索研究其動(dòng)力學(xué)特點(diǎn)具有重要意義。

對(duì)轉(zhuǎn)子系統(tǒng)進(jìn)行動(dòng)力特性研究經(jīng)常采用傳遞矩陣法或有限元法。因有限元法能對(duì)較復(fù)雜的轉(zhuǎn)子系統(tǒng)進(jìn)行完整而精確的幾何建模，容易保證計(jì)算結(jié)果的準(zhǔn)確性，同時(shí)計(jì)算機(jī)技術(shù)的飛速發(fā)展又為有限元法的計(jì)算效率提供了保障，在現(xiàn)代較復(fù)雜的轉(zhuǎn)子系統(tǒng)動(dòng)力特性計(jì)算中越來(lái)越多采用有限元法[8-9]。當(dāng)前最為流行的有限元分析軟件ANSYS功能十分強(qiáng)大，還很好地解決了動(dòng)力特性分析中的“陀螺效應(yīng)”影響的問(wèn)題。下文即以ANSYS為工具，分析磁懸浮轉(zhuǎn)子系統(tǒng)的動(dòng)力特性及規(guī)律。

1 轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)及參數(shù)

低溫制氧高速透平膨脹機(jī)的磁懸浮轉(zhuǎn)子系統(tǒng)的結(jié)構(gòu)如圖1所示。該轉(zhuǎn)子由兩個(gè)徑向電磁軸承和一個(gè)軸向電磁軸承支承，其中軸向電磁軸承的兩個(gè)電磁鐵對(duì)稱(chēng)安裝在轉(zhuǎn)子中央推力盤(pán)的左右兩側(cè)。徑向電磁軸承的初始結(jié)構(gòu)參數(shù)：氣隙寬度x0=0.17 mm，磁極數(shù)為8，單個(gè)磁極面積S0=1.32×10-4mm2，每極線圈匝數(shù)N0=42，偏磁電流I0=1A。電磁軸承控制器由PID調(diào)節(jié)器、傳感器、功率放大器組成。

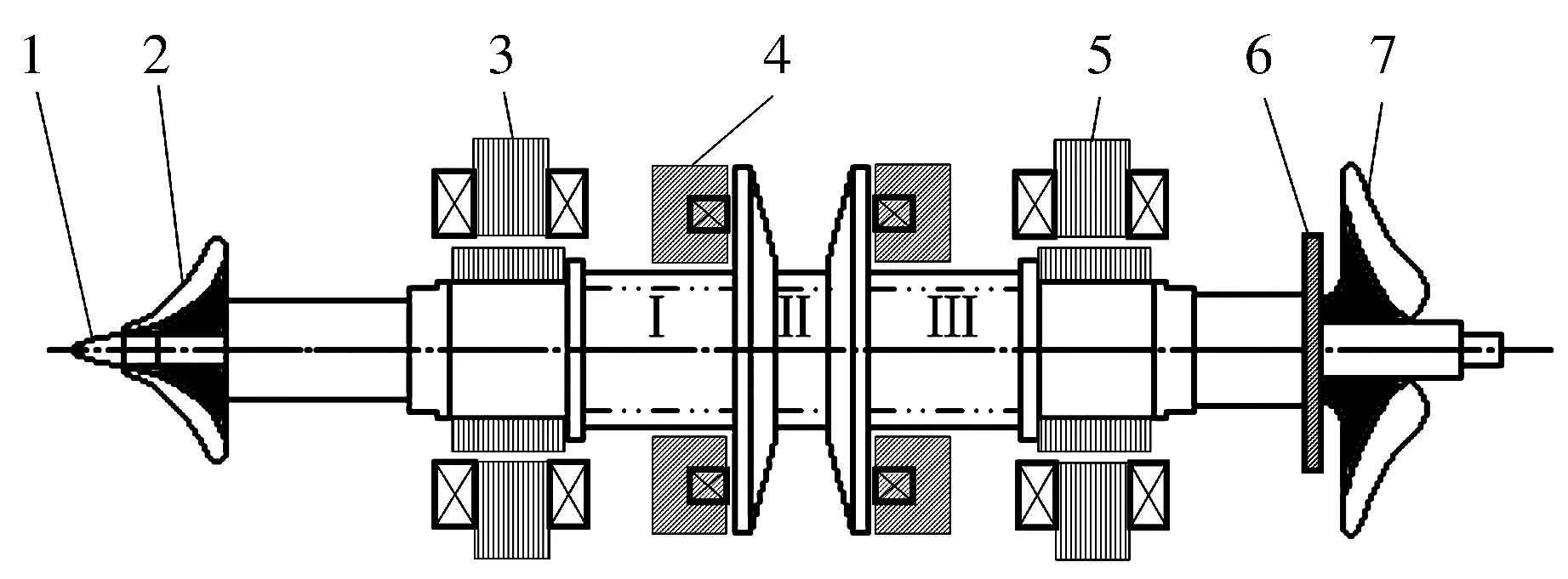
1—圓頭小螺帽；2—工作風(fēng)輪；3—左徑向磁軸承；4—軸向磁軸承；5—右徑向磁軸承；6—軸向定位墊片；7—平衡風(fēng)輪圖1 透平膨脹機(jī)磁懸浮轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)示意圖

該轉(zhuǎn)子的設(shè)計(jì)轉(zhuǎn)速是1.08×105r/min。為考察該轉(zhuǎn)子是否能安全達(dá)到工作轉(zhuǎn)速并穩(wěn)定運(yùn)轉(zhuǎn)以及在工作轉(zhuǎn)速范圍內(nèi)系統(tǒng)的振動(dòng)特點(diǎn)，故將分析的轉(zhuǎn)速范圍定在0～1.2×105r/min(0～2 kHz),即計(jì)算從零到稍高于工作轉(zhuǎn)速的整個(gè)轉(zhuǎn)速范圍內(nèi)的各階臨界轉(zhuǎn)速與模態(tài)振型。

2 剛度及阻尼系數(shù)的計(jì)算

工程應(yīng)用的電磁軸承轉(zhuǎn)子系統(tǒng)多為5自由度磁懸浮系統(tǒng)，包含兩個(gè)徑向電磁軸承和一個(gè)軸向電磁軸承，為轉(zhuǎn)子提供除繞軸旋轉(zhuǎn)以外的其余5個(gè)自由度的控制。低溫制氧高速透平膨脹機(jī)的磁懸浮轉(zhuǎn)子系統(tǒng)也不例外，其控制系統(tǒng)各自由度的定義如圖2所示。徑向電磁軸承1和2分別對(duì)應(yīng)x1，y1和x2，y2方向的控制通道，軸向電磁軸承則對(duì)應(yīng)z方向的控制通道。

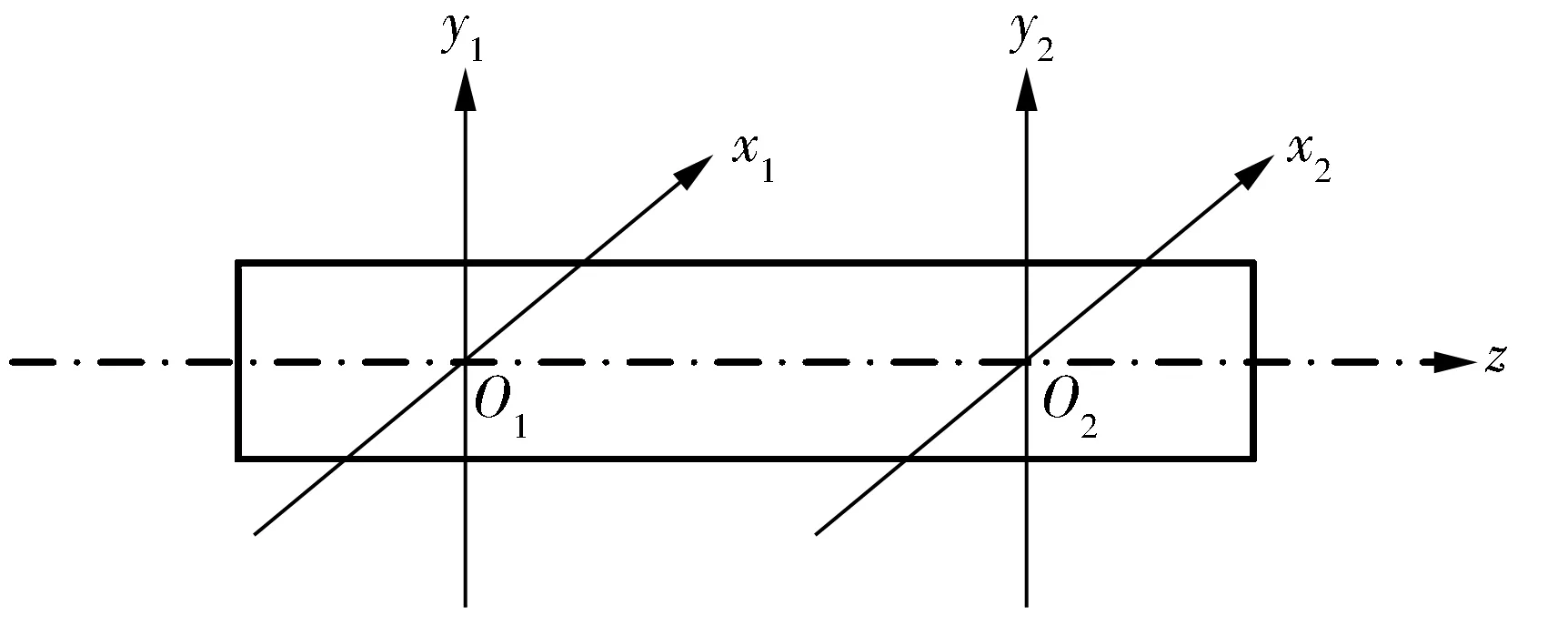
圖2 轉(zhuǎn)子的5自由度控制示意圖

由文獻(xiàn)[10]知，徑向電磁軸承一般視為正交各向異性的軸承，故每個(gè)徑向電磁軸承需要計(jì)算兩個(gè)正交方向的剛度與阻尼系數(shù)。另外，電磁軸承交叉剛度與阻尼系數(shù)的計(jì)算與選用的傳感器類(lèi)型和安裝等具體情況有關(guān)[11]。由于通常情況下電磁軸承氣隙寬度與轉(zhuǎn)子直徑之比很小，計(jì)算出的電磁軸承交叉剛度和阻尼系數(shù)也很小，故其對(duì)轉(zhuǎn)子動(dòng)力特性的影響可以不予考慮[12]。因此，完整的5自由度磁懸浮系統(tǒng)動(dòng)力特性計(jì)算中需要計(jì)算5組剛度與阻尼系數(shù)，即(kxx1,cxx1)，(kyy1,cyy1)，(kxx2,cxx2)，(kyy2,cyy2)和(kz,cz)。

每組剛度與阻尼系數(shù)的計(jì)算公式為：

(1)

式中：ke為對(duì)應(yīng)方向的等效剛度系數(shù)；ce為對(duì)應(yīng)方向的等效阻尼系數(shù)；ω為輸入控制器的信號(hào)頻率；Gc(jω)為控制器對(duì)應(yīng)方向傳遞函數(shù)；kx為電磁軸承的位移剛度系數(shù)；ki為系統(tǒng)的電流剛度系數(shù)；μ0為真空磁導(dǎo)率；S0為氣隙截面積；N為電磁(軸承)線圈的匝數(shù)；I0為偏磁電流分量；x0為轉(zhuǎn)子懸浮時(shí)軸承氣隙的設(shè)計(jì)長(zhǎng)度。

從上述計(jì)算式看，電磁軸承的剛度及阻尼系數(shù)除與kx，ki(由軸承結(jié)構(gòu)參數(shù)計(jì)算確定)有關(guān)外，還與控制器的傳遞函數(shù)及信號(hào)頻率ω有關(guān)。

3 系統(tǒng)臨界轉(zhuǎn)速和模態(tài)振型的計(jì)算

在ANSYS中創(chuàng)建該轉(zhuǎn)子系統(tǒng)完整的三維幾何模型，并指定單元類(lèi)型，設(shè)置材料屬性，然后劃分網(wǎng)格，生成有限元模型。

將每個(gè)電磁軸承模擬為具有剛度系數(shù)和阻尼系數(shù)的彈性阻尼支承，以COMBIN14單元來(lái)模擬，并設(shè)置相應(yīng)的實(shí)常數(shù)(剛度和阻尼系數(shù))。

在每個(gè)彈簧單元的外端施加“ALL DOF”約束(完全固接)，內(nèi)端自由。施加約束后的整個(gè)系統(tǒng)有限元模型如圖3所示。

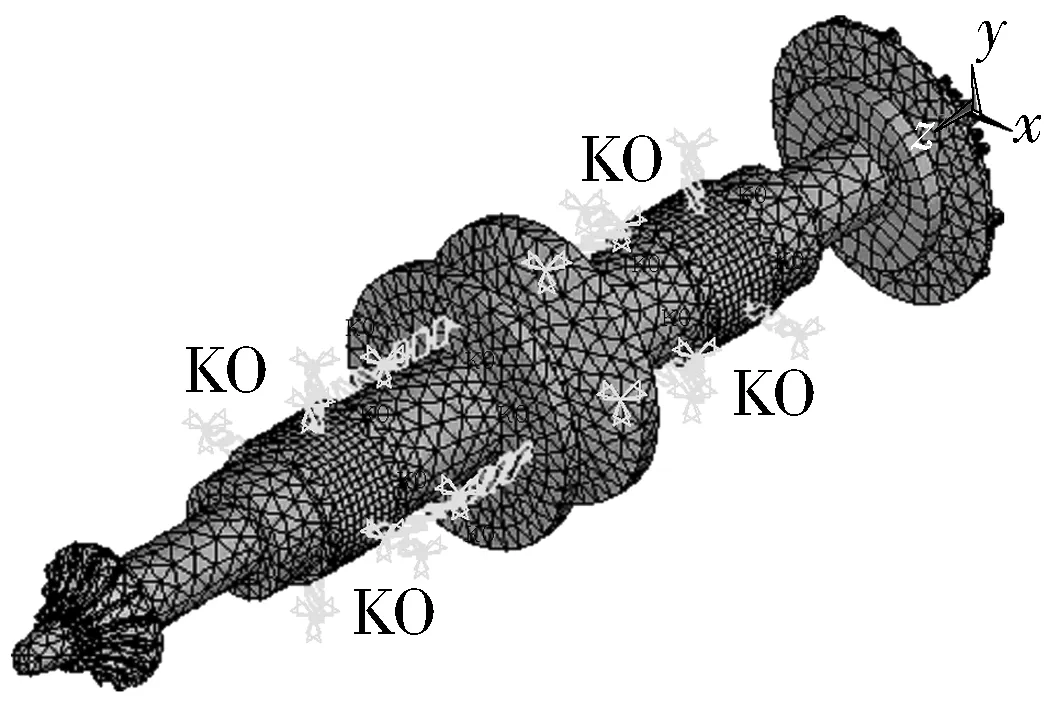
圖3 施加約束后的轉(zhuǎn)子系統(tǒng)有限元模型

求解得到系統(tǒng)的前8階固有頻率和模態(tài)振型。

上述計(jì)算過(guò)程只是在電磁軸承的一組特定剛度與阻尼系數(shù)下的ANSYS分析過(guò)程。但由于電磁軸承的剛度及阻尼系數(shù)是轉(zhuǎn)子渦動(dòng)頻率的函數(shù)，當(dāng)渦動(dòng)頻率發(fā)生改變時(shí)，電磁軸承的剛度及阻尼系數(shù)需要重新計(jì)算，由計(jì)算出來(lái)的新的剛度及阻尼系數(shù)代入ANSYS開(kāi)始新的模態(tài)分析，得到新的固有頻率和模態(tài)振型。

需要指出的是，轉(zhuǎn)子的渦動(dòng)情況很復(fù)雜，這里只考慮最常見(jiàn)和最主要的正向同步渦動(dòng)，只有當(dāng)計(jì)算出的固有頻率與轉(zhuǎn)子的渦動(dòng)頻率相等時(shí)對(duì)應(yīng)的轉(zhuǎn)速才是臨界轉(zhuǎn)速。因此，需要計(jì)算工作轉(zhuǎn)速范圍內(nèi)一系列轉(zhuǎn)速下的固有頻率和模態(tài)振型，然后將各次模態(tài)分析得到的固有頻率匯總整理，繪制出各階固有頻率隨渦動(dòng)速度的變化曲線。

4 臨界轉(zhuǎn)速和模態(tài)振型計(jì)算結(jié)果及影響分析

4.1 計(jì)算結(jié)果

控制器參數(shù)如表1所示。各階固有頻率曲線如圖4所示。圖中各階固有頻率曲線與45°直線的交點(diǎn)所對(duì)應(yīng)的轉(zhuǎn)速即為正向同步渦動(dòng)的各階臨界轉(zhuǎn)速(為清晰起見(jiàn)，列于表2)，其對(duì)應(yīng)的振型即為臨界振型。模態(tài)振型計(jì)算結(jié)果如圖5所示。需要指出的是，此處的8階固有頻率與傳統(tǒng)轉(zhuǎn)子動(dòng)力學(xué)意義上的有關(guān)概念不同，僅是為了敘述方便，按固有頻率從小到大排列為1階、2階、3階等。若按傳統(tǒng)轉(zhuǎn)子動(dòng)力學(xué)的意義，7，8階才是真正的1階固有頻率。

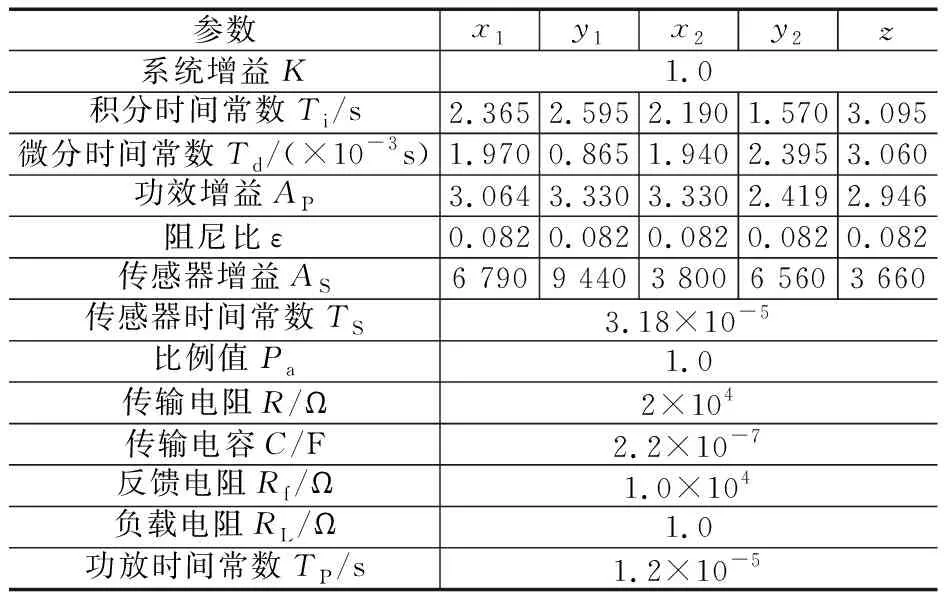
表1 各通道方向的控制器參數(shù)

表2 按初始參數(shù)計(jì)算的各階臨界轉(zhuǎn)速 ×103r/min

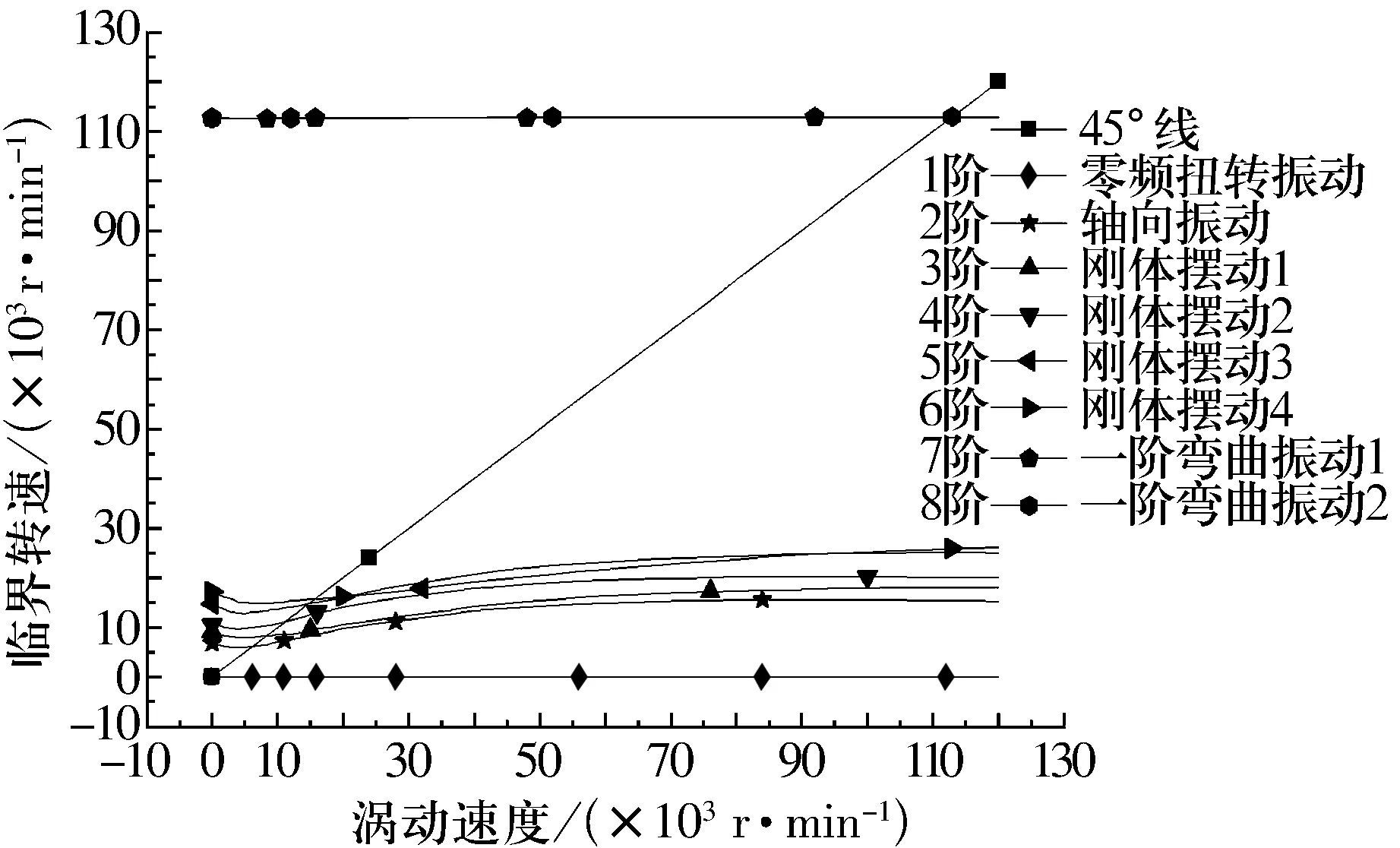
圖4 按初始參數(shù)計(jì)算的各階固有頻率變化曲線

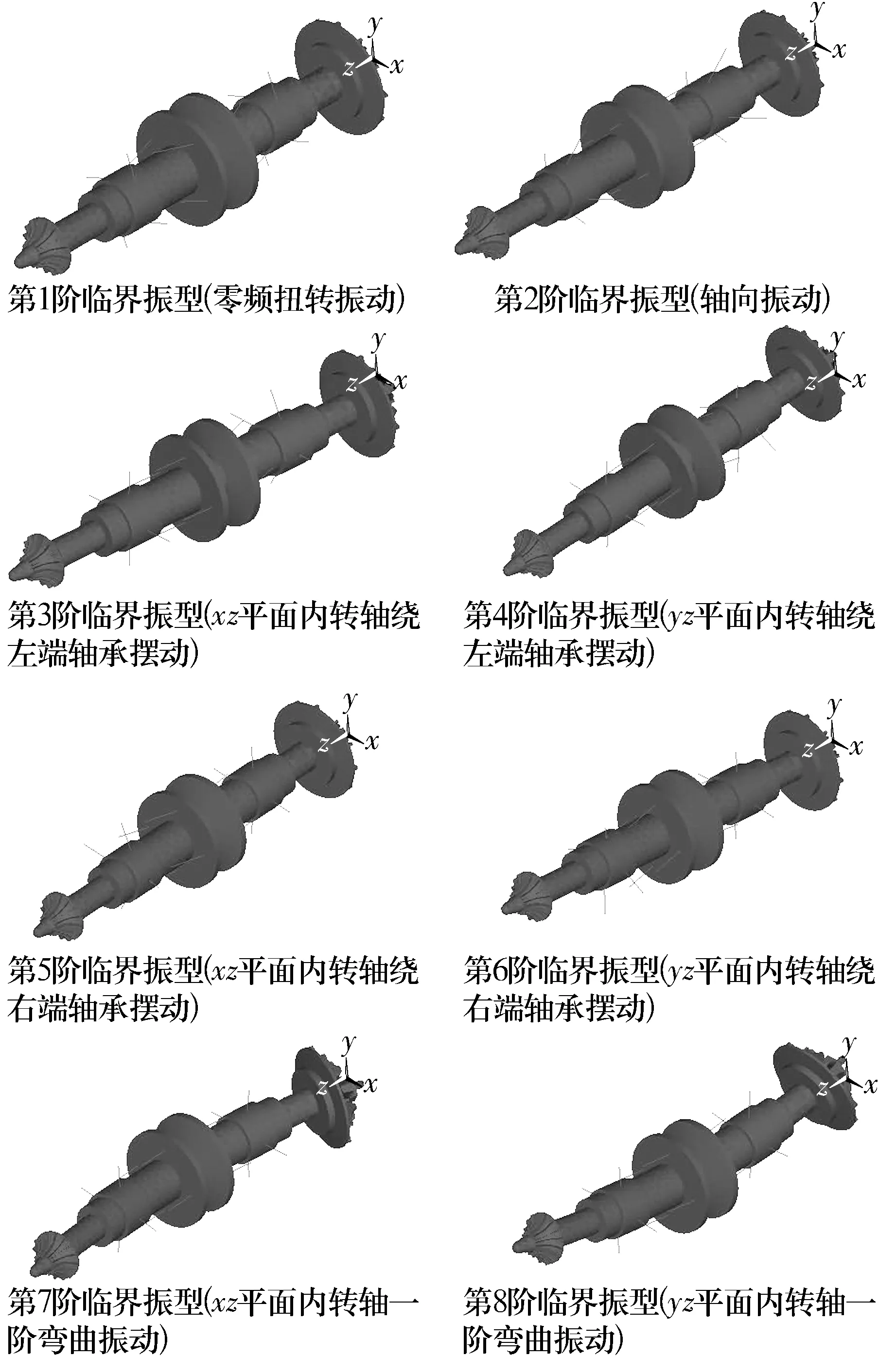
圖5 按初始參數(shù)計(jì)算的各階模態(tài)振型圖

由該組計(jì)算結(jié)果可知，系統(tǒng)在計(jì)算的頻率范圍內(nèi)(0～2 kHz)存在8階臨界轉(zhuǎn)速(固有頻率)，對(duì)應(yīng)8階模態(tài)振型。由圖5的臨界振型知，除1階扭轉(zhuǎn)振動(dòng)和2階軸向平動(dòng)以外，第3，4，5，6階都是剛體擺動(dòng)，其振動(dòng)頻率都在100～300 Hz。其中3階與4階、5階與6階分別是一對(duì)正交的模態(tài)振型。7階、8階是一階彎曲模態(tài)振型，也是一對(duì)正交模態(tài)。圖4反映了各階固有頻率與轉(zhuǎn)軸渦動(dòng)速度(轉(zhuǎn)速)之間的變化規(guī)律。2，3，4，5，6階曲線隨渦動(dòng)速度的提高變化明顯，說(shuō)明這5階固有頻率受軸承剛度影響較大。而由圖5的模態(tài)振型可以看出，這5階振動(dòng)與電磁軸承5個(gè)控制自由度z，x1，y1，x2，y2有一一對(duì)應(yīng)的關(guān)系。因此可以說(shuō)2，3，4，5，6階固有頻率是由電磁軸承各控制自由度方向的剛度來(lái)決定的。7，8階曲線基本重合，位于圖的上部，幾乎呈水平直線， 說(shuō)明7，8階固有頻率隨著轉(zhuǎn)速的提高沒(méi)有明顯改變，其幾乎不受軸承剛度的影響。從表2可知，前6個(gè)臨界轉(zhuǎn)速遠(yuǎn)小于設(shè)計(jì)轉(zhuǎn)速，是安全的；而7，8階臨界轉(zhuǎn)速則與設(shè)計(jì)轉(zhuǎn)速比較接近，分別與設(shè)計(jì)轉(zhuǎn)速相差4.4%和4.5%，不符合工程上對(duì)臨界轉(zhuǎn)速的安全性要求。

4.2 影響因素

4.2.1 軸承半徑氣隙

為考察電磁軸承半徑氣隙大小(最重要的軸承結(jié)構(gòu)參數(shù))對(duì)系統(tǒng)臨界轉(zhuǎn)速和模態(tài)振型的影響，改變軸承氣隙寬度x0，取x0=0.15 mm，其余參數(shù)均不變。得到的各階固有頻率變化曲線與圖4完全類(lèi)似，表3列出了具體的臨界轉(zhuǎn)速數(shù)值。而模態(tài)振型計(jì)算結(jié)果同圖5。

表3 改變軸承氣隙寬度計(jì)算的各階臨界轉(zhuǎn)速 ×103r/min

從表3可知，除零頻的扭轉(zhuǎn)振動(dòng)不變以外，其余2，3，4，5，6，7，8階臨界轉(zhuǎn)速分別提高了14.52%，10.46%，17.77%，14.42%，10.70%，0.05%，0.06%。可見(jiàn)，當(dāng)軸承氣隙寬度x0從0.17 mm改為0.15 mm時(shí)，因電磁軸承各自由度的剛度增加，各臨界轉(zhuǎn)速都得到提高。其中2，3，4，5，6階臨界轉(zhuǎn)速增幅較大，7，8階沒(méi)有明顯增加。

4.2.2 控制器參數(shù)

改變控制器參數(shù)，如表4所示，軸承結(jié)構(gòu)參數(shù)不變。計(jì)算得到的各階固有頻率變化曲線如圖6所示；臨界轉(zhuǎn)速具體數(shù)值如表5所示。而模態(tài)振型計(jì)算結(jié)果仍與圖5一樣。

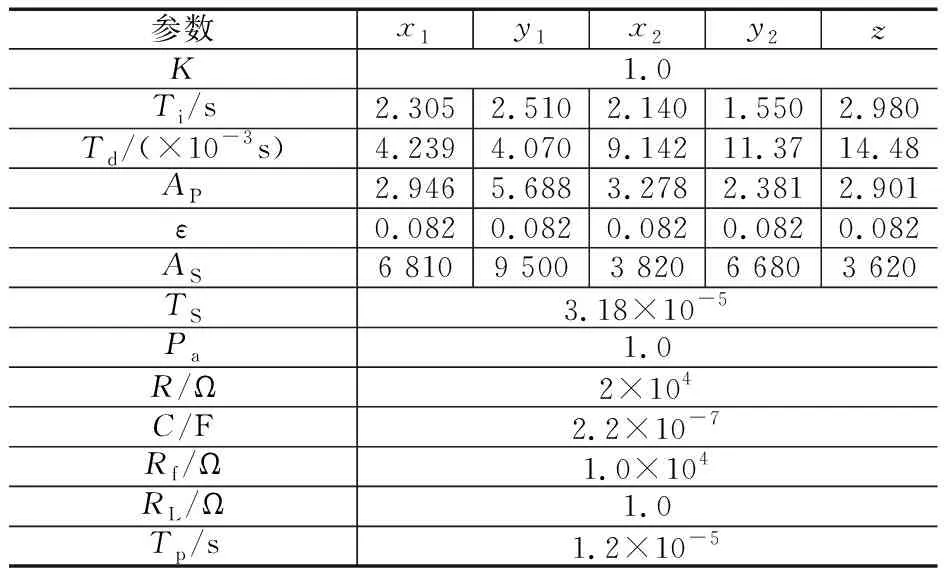
表4 改變后的各通道方向的控制器參數(shù)

表5 改變控制器參數(shù)計(jì)算的各階臨界轉(zhuǎn)速 ×103r/min

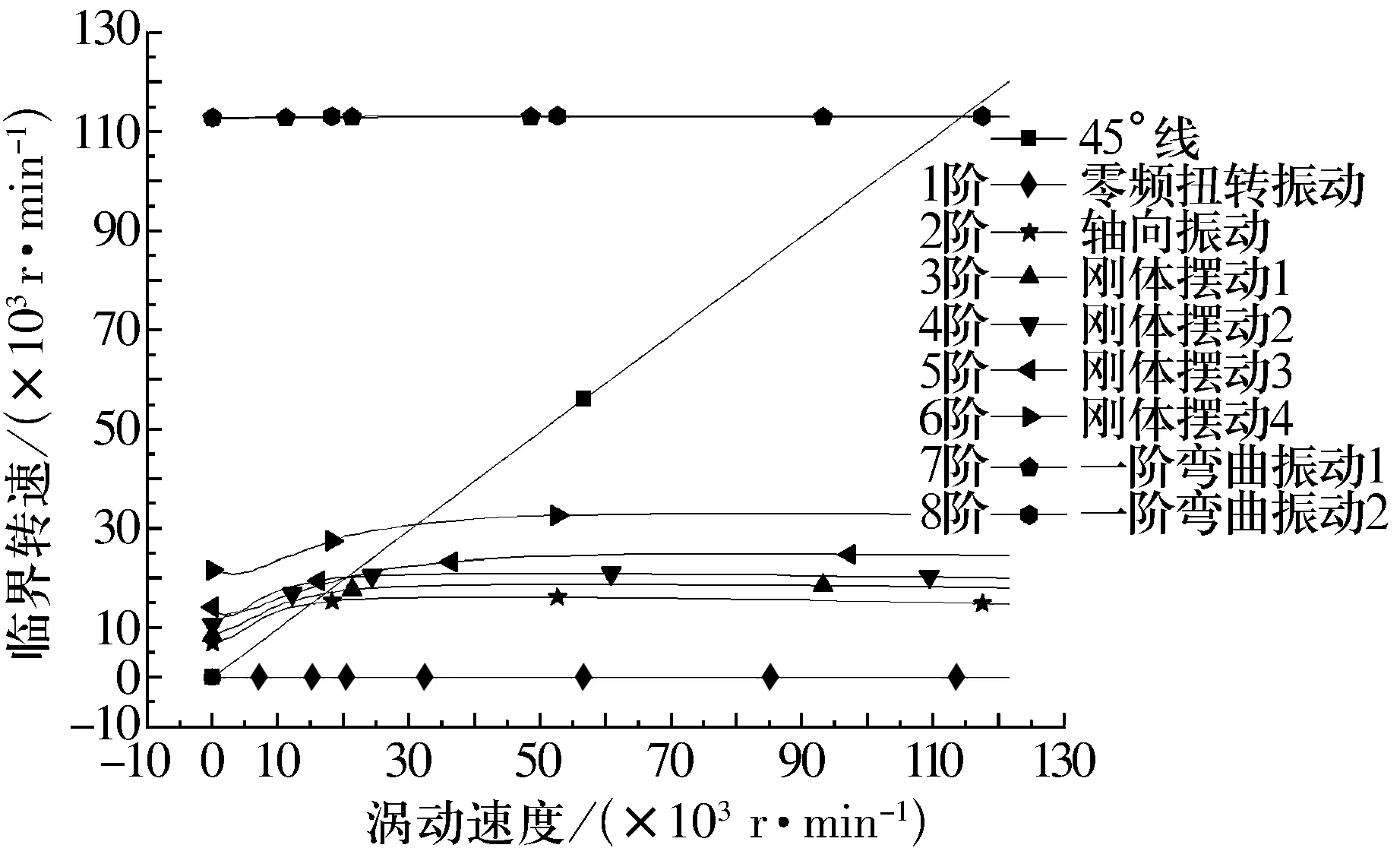
圖6 改變控制器參數(shù)的各階固有頻率變化曲線

僅改變控制器參數(shù)時(shí)，得到的電磁軸承的剛度阻尼系數(shù)有明顯變化。對(duì)比圖6與圖4可知，各固有頻率曲線的總體變化規(guī)律沒(méi)有改變；而2，3，4，5，6階固有頻率曲線的形狀和排列順序有所改變。計(jì)算得到的各階模態(tài)振型形狀基本同前；只是振幅稍有改變，各階順序有所改變。這是由控制器參數(shù)改變后引起各控制自由度剛度大小改變和順序重新排列所致。這也再次證明了該轉(zhuǎn)子系統(tǒng)的2，3，4，5，6階振動(dòng)完全是由軸承決定的，且與控制器5個(gè)控制自由度有著準(zhǔn)確的一一對(duì)應(yīng)關(guān)系，其對(duì)應(yīng)的臨界轉(zhuǎn)速是“軸承主導(dǎo)型”臨界轉(zhuǎn)速，振動(dòng)模態(tài)也是“軸承主導(dǎo)型”振動(dòng)模態(tài)。由表5與表2的對(duì)比看出，臨界轉(zhuǎn)速除扭轉(zhuǎn)振動(dòng)不變以外，其余各階都提高了。其中2，3，4，5，6階臨界轉(zhuǎn)速變化幅度很大，其是由控制器參數(shù)大幅變化所致，7，8階臨界轉(zhuǎn)速仍沒(méi)有明顯增加。

4.2.3 轉(zhuǎn)子結(jié)構(gòu)

從上述計(jì)算結(jié)果可以看出，無(wú)論怎樣改變軸承結(jié)構(gòu)參數(shù)和控制器參數(shù)，7，8階臨界轉(zhuǎn)速都沒(méi)有明顯改變，始終離設(shè)計(jì)工作轉(zhuǎn)速很近，以轉(zhuǎn)子系統(tǒng)現(xiàn)有的結(jié)構(gòu)條件是不能在設(shè)計(jì)工作轉(zhuǎn)速下安全運(yùn)轉(zhuǎn)的。看來(lái)要顯著改變7，8階臨界轉(zhuǎn)速，只有改變轉(zhuǎn)子本身的結(jié)構(gòu)，通過(guò)增加或降低轉(zhuǎn)子的剛度，使臨界轉(zhuǎn)速遠(yuǎn)離工作轉(zhuǎn)速。經(jīng)研究計(jì)算，如圖1所示，減小圖1轉(zhuǎn)子上Ⅰ，Ⅱ，Ⅲ 3段的直徑，其中實(shí)線表示原來(lái)的軸段，直徑均為26 mm；雙點(diǎn)劃線表示改變后的軸段，直徑均變?yōu)?0 mm。軸承結(jié)構(gòu)參數(shù)與控制器參數(shù)不變。改變轉(zhuǎn)子結(jié)構(gòu)后，計(jì)算得到的模態(tài)振型仍同圖5，臨界轉(zhuǎn)速的計(jì)算數(shù)值如表6所示。

表6 改變轉(zhuǎn)子結(jié)構(gòu)計(jì)算的各階臨界轉(zhuǎn)速 ×103r/min

從表6可知，轉(zhuǎn)子改小后，系統(tǒng)的7，8階臨界轉(zhuǎn)速已經(jīng)大幅降低，都低于工作轉(zhuǎn)速23%，符合工程上對(duì)臨界轉(zhuǎn)速的安全性要求。其余各階臨界轉(zhuǎn)速變化不大，都離開(kāi)工作轉(zhuǎn)速足夠遠(yuǎn)，都能安全越過(guò)。所以此改造方案是可行的。這也再次證明了7，8階臨界轉(zhuǎn)速主要受轉(zhuǎn)子結(jié)構(gòu)影響。

綜合以上分析，軸承的結(jié)構(gòu)參數(shù)與控制器參數(shù)的改變會(huì)使幾個(gè)低階臨界轉(zhuǎn)速(對(duì)應(yīng)轉(zhuǎn)子的剛體平動(dòng)與擺動(dòng)模態(tài))的大小發(fā)生明顯變化；而轉(zhuǎn)子結(jié)構(gòu)的改變能引起高階臨界轉(zhuǎn)速(對(duì)應(yīng)轉(zhuǎn)子的彎曲振動(dòng)模態(tài))的顯著改變。各種情況下系統(tǒng)模態(tài)振型形狀都不變。可以推斷：電磁軸承轉(zhuǎn)子系統(tǒng)在經(jīng)過(guò)幾個(gè)低階剛體運(yùn)動(dòng)模態(tài)以后，其模態(tài)振型才開(kāi)始呈現(xiàn)1階彎曲、2階彎曲等振動(dòng)模態(tài)，對(duì)應(yīng)的臨界轉(zhuǎn)速主要受轉(zhuǎn)子結(jié)構(gòu)的影響，這才是傳統(tǒng)轉(zhuǎn)子動(dòng)力學(xué)意義上的臨界轉(zhuǎn)速。這是因?yàn)椋?dāng)轉(zhuǎn)子轉(zhuǎn)速增大時(shí)，軸承剛度阻尼的影響逐漸減少，轉(zhuǎn)子特性的影響逐漸增大，此時(shí)系統(tǒng)的動(dòng)力學(xué)特性逐漸向傳統(tǒng)的動(dòng)力學(xué)特性逼近。事實(shí)上，在前面的計(jì)算中，當(dāng)提取的模態(tài)數(shù)增加時(shí)，可以發(fā)現(xiàn)后面接著就是傳統(tǒng)意義上的2階和3階等彎曲振動(dòng)模態(tài)，而且都是位于兩個(gè)正交平面內(nèi)，成對(duì)出現(xiàn)，這完全符合傳統(tǒng)轉(zhuǎn)子動(dòng)力學(xué)的特點(diǎn)。只是因?yàn)檫@時(shí)的臨界轉(zhuǎn)速已經(jīng)很高，超出本實(shí)例中的設(shè)計(jì)工作轉(zhuǎn)速很多，所以本文未列出。

5 實(shí)例對(duì)比

對(duì)電磁軸承支承的透平膨脹機(jī)樣機(jī)進(jìn)行過(guò)多次試驗(yàn)[13]。以初始參數(shù)計(jì)算結(jié)果為例，試驗(yàn)觀察到的臨界轉(zhuǎn)速與有限元計(jì)算結(jié)果對(duì)比如表7所示。試驗(yàn)中觀察到的幾個(gè)臨界轉(zhuǎn)速與有限元計(jì)算值非常接近，表明有限元分析方法是正確可靠的。

表7 臨界轉(zhuǎn)速有限元計(jì)算值與試驗(yàn)值的對(duì)比 ×103r/min

6 結(jié)論

(1) 由于電磁軸承特殊的控制方式——分通道控制，其轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)特性計(jì)算中包含幾個(gè)由軸承本身產(chǎn)生的低階臨界轉(zhuǎn)速及其相應(yīng)的振動(dòng)模態(tài)。這幾個(gè)低階振動(dòng)模態(tài)都是剛體運(yùn)動(dòng)模態(tài)，其數(shù)目和形態(tài)與軸承控制器的幾個(gè)控制通道一一對(duì)應(yīng)。因此相應(yīng)的臨界轉(zhuǎn)速大小主要受電磁軸承的影響，即為“軸承主導(dǎo)型”臨界轉(zhuǎn)速，可以通過(guò)改變電磁軸承的結(jié)構(gòu)參數(shù)和控制器相應(yīng)控制通道的參數(shù)來(lái)精確調(diào)節(jié)。

(2) 電磁軸承轉(zhuǎn)子系統(tǒng)在經(jīng)過(guò)低階剛體振動(dòng)模態(tài)以后，接著就呈現(xiàn)1階彎曲、2階彎曲、3階彎曲等振動(dòng)模態(tài)，所對(duì)應(yīng)的臨界轉(zhuǎn)速主要受轉(zhuǎn)子結(jié)構(gòu)的影響，是“轉(zhuǎn)子主導(dǎo)型”臨界轉(zhuǎn)速，這才是傳統(tǒng)轉(zhuǎn)子動(dòng)力學(xué)意義上的臨界轉(zhuǎn)速。此后的動(dòng)力學(xué)特性就和傳統(tǒng)的軸承轉(zhuǎn)子系統(tǒng)一樣。