大功率永磁電機溫度場數值計算及實測對比

劉萬平 張新麗 趙祥 張世福

(新疆金風科技股份有限公司，新疆 烏魯木齊 830026)

1 引言

電機運行時會在線圈、鐵心等部件上產生能量損耗，這部分損耗最終都將以熱能的形式散發出去。如果電機的通風冷卻設計不合理，就會使電機內部溫度不能保持在合理的范圍內，溫升過高會導致絕緣老化，長時間運行時會使絕緣電氣性能下降；同時局部溫升不均勻，還會產生很大的熱應力，造成電機結構上的永久性損害，最終導致的發電機故障，會直接影響用戶的使用。因而溫升是考核同步電機的一個重要指標。

目前溫升的主要計算方法有三種：簡化公式法[1]、等效熱路法[2]和溫度場法[3-4]。簡化公式法是電機制造廠常用方法，首先計算出各部分的熱負載，再通過牛頓散熱公式得到相應的溫升值。這種方法計算簡單，但只能計算電機的平均溫升，計算結果不太精確。等效熱路法是根據傳熱學和電路理論來形成等效熱路，熱路圖中的熱源為繞組的銅損耗和鐵損耗，這些損耗所在部件在計算中認為是均質的。損耗熱量通過各種相應的熱阻，由熱源向冷卻介質傳遞，形成一個復雜的熱網絡。此方法計算精度要高于簡化公式法，但如果提高精度，必需增加網絡節點和熱阻數，使工作量增大[5-6]。溫度場是現代數值方法來求解熱傳導方程，將求解區域離散成許多小單元后，在每個單元中建立方程，再對總體方程組進行求解。其優點是將研究對象從總體轉為局部單元，使每個局部單元都能獲得可靠的計算數據，從而更加準確合理地指導電機設計，缺點是計算量大，不適合用在設計初期的選型計算中。

本文以金風科技股份有限公司自主研發的3MW永磁同步發電機為實例，重點介紹熱路法，并分別采用熱路法和有限元方法對其在不同負載條件下的溫度場進行了計算，并將計算結果與實測數據進行了對比，驗證了熱路法的可行性。

2 熱路法計算發電機溫升

2.1 基礎理論

一個實體熱源可通過三維空間上不同的面將熱量傳送出去。假設圖1所示的均勻發熱體內單位時間的發熱量為P，其內部中心溫升為T，發熱體的熱導率為λ，則可近似認為單位時間的等效熱流量P將會沿著xyz六個方向傳送出去。

假設通過x正方向傳送的熱量為Px，壁面溫度為Tx1，則試驗證明，傳過平壁的每單位時間熱量Px與面積S，溫度差（T-Tx1）成正比，與壁厚（Lx/2）成反比[7]，即：

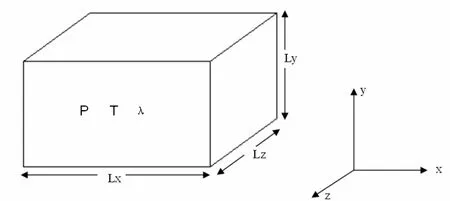
圖1 發熱量為P的均勻發熱體

式1即為熱傳導基本定律。

這樣，類似歐姆定律，可以將溫差看做是電路中的電壓，單位時間的傳輸熱量相當于電路中的電流，而熱阻則相當于電路中的電阻。如果我們把電機分為n個這樣的發熱體，則每個發熱體都可建立類似式1的方程，將n個方程聯合求解，在熱阻和熱流量已知的情況下，可求解得到各點溫度。如果電機離散成足夠多的單元，則計算精度可以滿足我們的要求。

我們也可從圖2中看到一個單元之間熱阻、溫度及熱流量之間的關系，即熱網絡圖。假設發熱體中的單位時間內所有熱流量P從i點注入整個系統，并等效從6個方向散發出去。每個方向所遇的熱阻可通過面積導熱率及壁厚得到，如式2。而-1/6Rx、-1/6Ry、-1/6Rz為各方向的耦合熱阻。

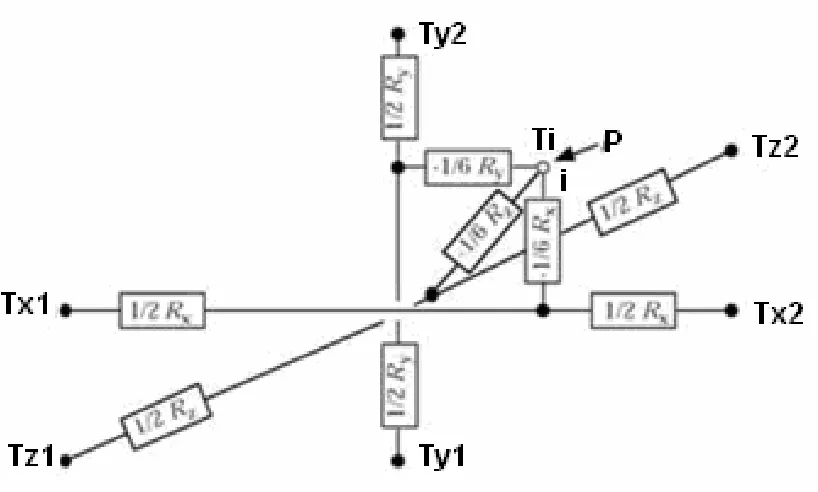
圖2 熱網絡圖

2.2 電機熱路場分析模型

本文中的算例電機為金風自主研發的3 MW風力發電機組用三相永磁同步發電機，電機額定功率為3200 kW。冷卻方式為IC666[8]，即電機為空空冷卻，一次冷卻介質空氣在獨立外裝風扇的作用下強迫電機內部空氣循環流動，二次冷卻介質為電機周圍環境介質，也在獨立外裝風扇的作用下驅動周圍冷卻空氣流動，從而使電機的發熱功率最終通過二次冷卻空氣帶走。

根據上述方法，對算例電機進行熱網絡分析，主要求解包括繞組、鐵心和磁鋼等地方的溫升，對電機的溫升設計進行校核。

在計算前做如下假設：

（1）電機定子共120個槽，以每個齒槽為一個單元，假設在圓周上單元與單元之間不存在熱交換， 而溫度差只在一個單元之內的齒、槽內分布；

（2）電機定子軸向均勻分成20段，為徑向通風冷卻，假設冷卻系統沿軸向完全對稱，鐵心段之間不存在熱交換，而兩端部繞組溫度場分布情況完全一致；

（3）電機內發熱部分僅存在于上、下層繞組、鐵心、轉子磁軛和磁鋼上，并假設為均勻發熱體，其它電機部件上無損耗；

（4）電機內部的熱流量方向為三維方向；

（5）電機所有冷卻氣體的溫升相同，并按照下式進行計算。

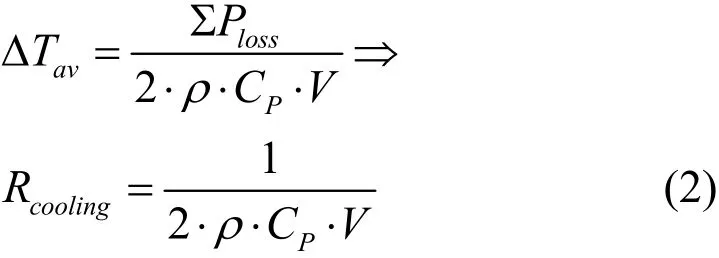
其中，V是氣體的總流量，經過磁鋼、繞組、定子齒部和轉子軛部后所有冷卻氣體的平均溫升為△Tav。

按照圖 2所示方法，將電機主要發熱體等效為熱網絡圖，并將并聯和串聯的熱阻進行簡化，這樣電機熱網絡圖可表示為圖3中的簡化模型。

圖3中所示各項的表示意義如下：

P1、P3、P9分別對應于軛部區域、齒部下層、和齒部上層單位時間等效熱流量；P2為槽底下對應的鐵心處單位時間等效熱流量；P10、P4分別對應上下層繞組槽內單位時間熱流量；P7、P8為磁鋼和轉子磁軛處的單位熱流量，P5、P6、P11為求解方程時所需要的虛擬連接點，此點的熱流量設為0。

圖 3中所有熱阻為簡化后的值，分別代表各發熱單元之間的等效熱阻。

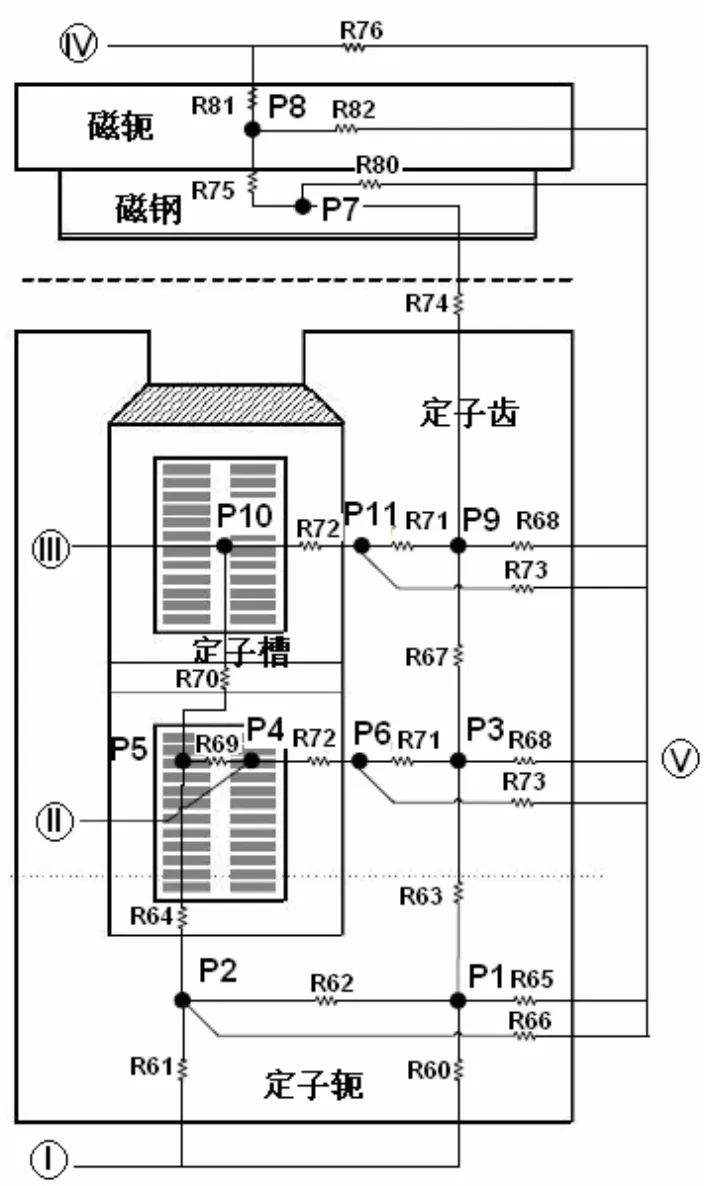
圖3 一個齒槽內的熱阻簡化模型

I表示定子外圓處的通風區域，II表示與下層繞組端部相連，III表示與上層繞組的端部相連，IV表示轉子內圓表面的區域，V表示與通風道相連的區域。

由于篇幅所限，在這里沒有給出繞組端部的等效熱網絡，其建模方式與定轉子建模方式相同。

2.3 計算過程與計算結果

根據電機實際運行環境及運行損耗，輸入如下接口參數：

表1 3 MW永磁發電機溫升計算接口參數

電機鐵心、繞組等各部件的導熱參數可根據查取相關材料特性手冊得到。而電機對流換熱系數的求解可分成三種，定轉子鐵心表面非強迫風冷的地方為自然對流換熱方式，因而求解得到的是自然對流換熱系數；通風道內（包含齒部、軛部、氣隙）等地方為強迫對流換熱方式，可根據風速求解得到相應的強迫對流換熱系數；而在端部由于線圈端部連接形式復雜，通常采用經驗系數來確定對流換熱系數。

3 有限元模型

有限元方法是目前用來計算電機溫升的常規方法，本文采用有限元方法，對3 MW永磁同步發電機的三維流場、溫度場進行計算。考慮幾何模型的對稱性，只對四分之一幾何模型進行分析，計算流體部分的流場分布。然后，從流體部分的流場分布中找到速度最小的流場通道，針對該通道進行網格局部劃分，并精細網格。采用 mpcci商業軟件進行流固耦合計算，分別用abaqus軟件進行固體部分計算，fluent軟件進行流體部分計算，從而達到整個流場的溫度分布。

網格剖分圖如圖 4。為了保證計算精度及考慮經濟性，采用全六面體網格劃分策略，此四分之一的電機模型需要網格數為400萬。

圖4 網格剖分圖

圖5中給出了溫度場計算結果，有限元計算結果與熱路法計算結果見表 2。可以看出除轉子磁軛外，絕大部分的平均溫升差值在 5℃以內。而之所以磁軛部分溫升相差較大，是由于熱路法計算中無法計及冷卻氣體經過電機不同部件后的溫度改變。在熱路法中，認為冷卻氣體的溫升均為經過所有部件后的平均溫升，因而經過磁軛時冷卻氣的溫升計算偏高，導致磁軛處的溫升比實際值偏大。

圖5 溫度場計算結果

4 實測對比

在全功率試驗臺上對3 MW永磁發電機做溫升試驗，試驗臺組成：兩臺1600 kW 的直流電動機并聯拖動齒輪箱1， 經扭矩儀（30000 Nm）、過渡支撐、萬向節、齒輪箱2、3 MW 永磁同步發電機、3MW ABB 變流器、升壓變壓器及調壓器后并入電網，其它設備包括電流互感器CT（精度0.2 級）等測試儀器。

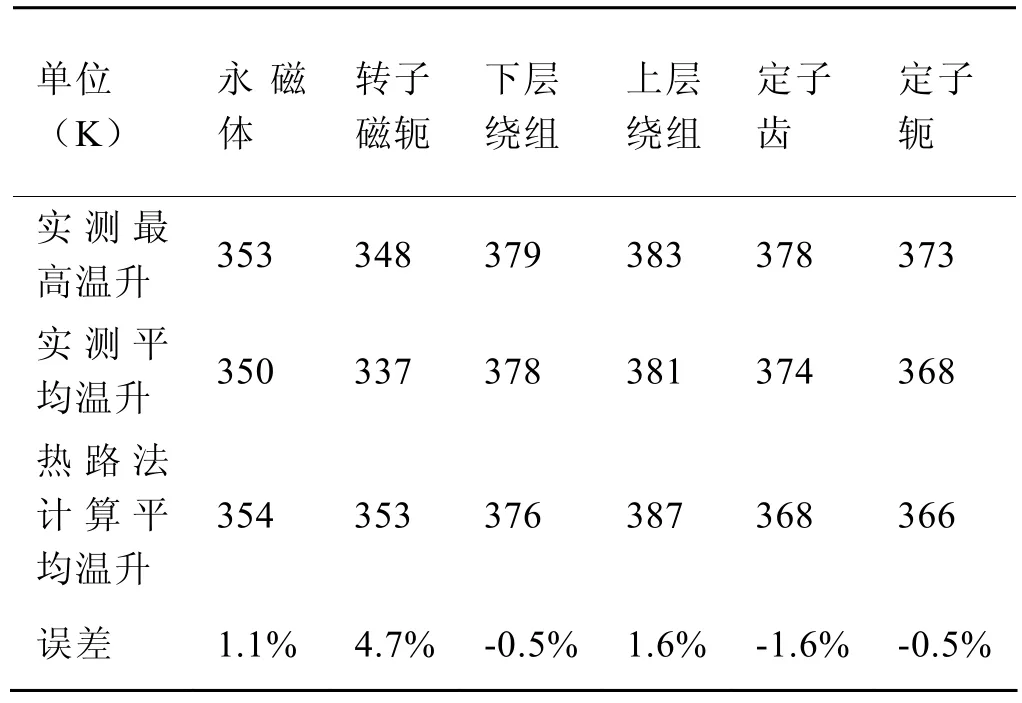
表2 熱路法與有限元法的計算對比

圖6 全功率試驗臺

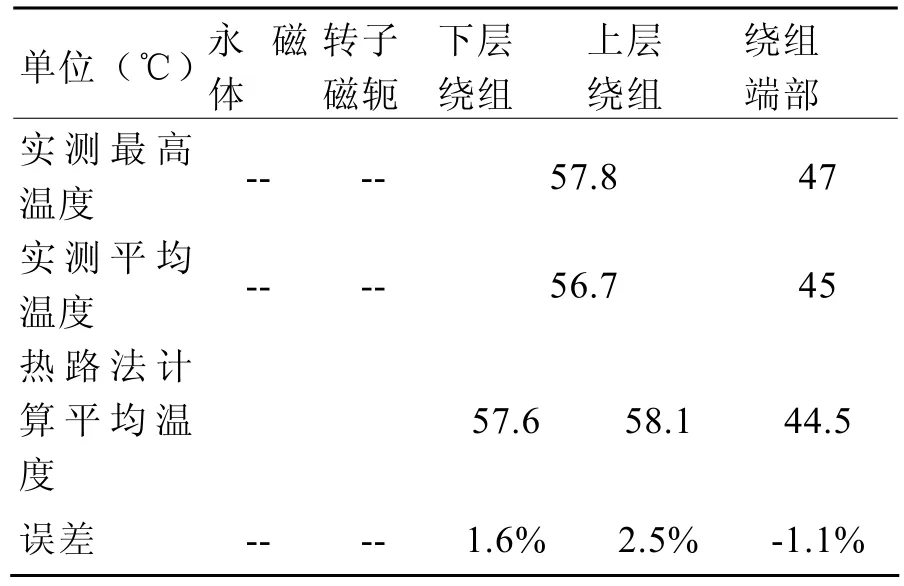
表3 熱路法計算與實測溫升數據對比

在電機溫升測量中，限于測試條件，通常只能在上下層繞組間以及繞組端部處埋設PT100傳感器，并根據PT100顯示的測試數據來判斷溫升是否超限。在本文的算例電機中，在繞組槽內和繞組端部處各均布放置了6個PT100。

由于受到電網限制，算例電機在試驗中限功率運行為2 MW，因而溫升數據為2 MW發電下的測量數據，為了對比，在熱路法進行計算時，也折算成2 MW功率下的發熱量，因而計算數據與實測數據具有可比性，表3中可以看出，測試與計算數據偏差很小，基本在2度以內。

5 結論

本文以金風科技股份有限公司自主研發的 3 MW永磁同步發電機為實例，分別采用熱路法和有限元方法對其在不同負載條件下的溫度場進行了計算，并將計算結果與實測數據進行了對比，證明了熱路法具有較高的精度，同時相比有限元法減少了計算量，可作為通風冷卻方案設計初期的選型方法。

[1] 李文宇. 同步電機熱計算與通風計算[J]. 船電技術,2007, 27(2): 72-75

[2] Juha Pyrho¨ nen, Tapani Jokinen and Vale′ ria Hrabovcova, Design of Rotating Electrical Machines[M]. John Wiley & Sons, Ltd, 2008.

[3] 陳志剛. 等效熱網絡法和有限元法在電機三維溫度場計算中的應用與比較[J]. 中小型電機, 1995. 22(1):3-6, 35

[4] 李廣德,何剛,何文秀.大型水輪發電機定子三維溫度場計算[J]. 大電機技術, 2000, 4(2): 1-5.

[5] 熊斌,大型水輪發電機內部流體場和溫度場的數值計算, 哈爾濱理工大學碩士學位論文: 2-4

[6] 李和明, 李俊卿. 電機中溫度計算方法及其應用綜述. 華北電力大學學報, 2005,32(1): 1-5

[7] 程福秀 林金銘. 現代電機設計[M]. 北京: 機械工業出版社.

[8] GB/T1993-1993，旋轉電機冷卻方法.