基于GPS的低軌衛星簡化解析法軌道預報*

柳青松,劉 峰,巨 濤

(航天恒星科技有限公司,北京100086)

0 引 言

星載GPS接收機由電源板、射頻板、定位板和軌道板等組成。定位板輸出用戶衛星的位置和速度等信息。軌道板軟件運行在星載高動態GPS接收機內部的DSP系統環境下,接收GPS接收機定位板輸出的位置、速度、時間等參數,進行軌道改進、預報,再將輸出值傳送給定位板,由GPS接收機將結果傳送給星務管理系統使用。目前,國內GPS接收機軌道板的主要用途是對定位結果進行平滑濾波和軌道預報。由于定位板的不穩定性、電離層閃爍或GPS衛星信號失鎖等因素的影響會導致定位板復位,此時軌道板預報便需實現數據中斷處的有效鏈接。一般情況下,定位板復位時間不超過10 min。單頻GPS接收機定位精度在10 m量級,而軌道板軟件主要是基于軌道動力學的卡爾曼濾波方法,短時間預報位置精度在20 m以內。軌道板進行軌道預報的目的是當定位板出現故障時進行軌道外推,而這種故障并不是經常發生,但軌道板軟件占用GPS接收機資源在60%以上,所以,在適當降低預報精度的條件下,應該盡可能地簡化軌道改進、預報和攝動計算公式,降低星載軟件的復雜度。

用一階分析攝動理論再增加考慮部分田諧項攝動來簡化解析法的公式。所謂一階分析攝動理論,就是在攝動計算時考慮一階短周期項、一階和二階長期項,而忽略10-6以上的短周期項和10-9以上的長期項。簡化過程就是根據該衛星及其軌道的具體特點,使得簡化后的軌道改進、攝動計算及預報基本上仍能達到一階分析攝動理論的精度。根據簡化的結果用C語言編寫源程序,仿真結果表明:該解析法考慮了主要的攝動項,算法簡單,計算速度快,能夠保證一定的計算精度,具有一定的工程應用意義。

某型號衛星軌道參數為軌道標高625 km,偏心率中心值在10-4量級。

1 基本原理

1.1 軌道改進[1-5]

軌道改進是在已知衛星狀態初值的情況下,利用較多的測量數據確定在一定意義下的最佳狀態估值。由于航天軟件的要求,在軌道改進方案中采用經典的微分軌道改進方法。

人造衛星繞地球運動所涉及的數學模型是一個非常復雜的非線性動力系統。在地心赤道坐標系中,衛星的運動方程可以表示為

在數學模型及相應的初始條件都是完全準確的情況下,積分上述方程可得到該運動方程的解為

由于數學模型無法完全準確,而且在實際工作中也得不到準確的初值,因此,需要通過一系列測量數據來修正各物理參數和初值。在數學模型和初值都不完全準確的情況下,衛星的坐標、速度可表示為

無論式(1)還是式(2)都是復雜的非線性方程,采用線性化后迭代求解的方法。式(2)線性化后可得方程

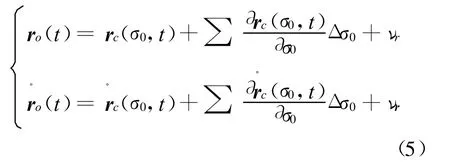
解上述方程可用最小二乘法。

1.2 攝動計算和軌道預報

如果地球是一個質量均勻的球體,則人造衛星在地球引力場中的運動方程可表示為

這是一個可積方程,衛星的運動軌道是一個確定的橢圓。但實際的地球形狀不規則、質量也不均勻,衛星的運動不僅受地球引力場作用,還受到大氣阻力、日月引力、太陽光壓等多種力的作用。由于除了主要的中心引力以外,其余的作用力都相對較小,可以把實際的衛星運動處理成攝二體問題,即一個簡單可積的二體問題加上攝動改正兩個部分[2]。

在人造衛星的攝動計算中,根據攝動計算的量級,若以地球中心引力為1,則通常把地球形狀扁率項J 2項作為一階小量(10-3),其余攝動,例如,帶諧項Jn(n≥3)、田諧項J lm(l≥2,m≥1)、大氣阻力、太陽光壓、日月引力、潮汐攝動以及由于坐標系本身運動產生的附加攝動均作為二階小量(10-6)[6]。

在本方案中攝動計算主要采用一階分析攝動,但增加了田諧項J 22、J 31 、J 32、J 33、J 41 、J 42、J 43、J 44。所謂一階理論,即考慮一階和二階長期項以及一階周期項。對于一般的近地衛星而言,田諧項Jlm(l≥2,m≥1)的攝動一般是二階短周期項。

軌道預報其實質就是一個攝動外推的過程。

2 簡化設計

2.1 完全不影響一階分析理論精度的簡化部分

一階短周期項是由于地球扁率項J 2(～10-3)引起的。在一階短周期項中,忽略含J2e的項,即忽略10-6以上的短周期項。

二階短周期項是由于帶諧項Jn(n≥2)、田諧項J lm(l≥2,m≥1)引起的。在二階短周期項中,僅考慮田諧項J 22、J 31、J 32、J 33的攝動系數中含有衛星平均運動角速度與地球自轉角速度的比值的項,即忽略10-6以上的短周期項。

一階長期項也是由于地球扁率項J 2引起的。在一階長期項中,忽略含 J 2e2的項,即忽略10-9以上的長期項。

對于J2引起的二階長期項(10-6),忽略含J22e的項,也是忽略10-9以上的長期項。

對于J n(n≥3,～10-6)引起的二階長期項,僅考慮J3,J4且忽略含J3e,J4e的項,也是忽略10-9以上的長期項。

對這顆衛星而言,光壓攝動是10-9量級,因此被忽略。

2.2 對精度影響不大,可以采取措施克服的簡化部分

忽略J n(n≥5)引起的二階長期項。

對于大氣阻力攝動(10-7～10-8),將僅考慮靜止球形大氣,并根據經驗估計將軌道近地點附近的大氣密度作為常數計算出來。其忽略的也是10-8～10-9以上的長期項。

對這顆衛星而言,由于βIn2I～10-8,日月引力攝動是10-8量級,由于程序量的限制,這部分也被忽略。

2.3 其它方面的簡化

合理地進行代碼設計,盡量避免不必要的浪費空間。盡量使用單精度數據,如輸入的觀測資料,其坐標、速度的精度均只有10-4～10-5量級,只有5～6位有效數字,用單精度表示不影響其精度,但可大量減少占用的存儲單元。

3 仿真及結果

采用根數系統為第一類無奇點根數系統

a,i,Ω,ξ=e cosω,

η=-e sinω,λ=ω+M

其中:a,i,Ω,e,ω,M為 Kepler根數,分別表示軌道半長徑、軌道傾角、升交點赤經、軌道偏心率、近地點輻角、平近點角。軌道改進結果為指定歷元時刻的軌道根數和衛星角速度的一階變化率。軌道預報的結果為指定時刻的地固坐標系下的衛星坐標。

軌道計算過程中采用坐標系為慣性坐標系,以地球質心為坐標原點,瞬時真赤道面為參考平面,X軸指向2000.0平春分點在真赤道上的投影。

程序中考慮了對異常值的處理問題,在沒有大量異常值的情況下,程序根據軌道改進的執行狀況按照三倍標準差的原則自行剔除大異常值,從而保證軌道改進的正常進行。并通過設置合理的收斂判別標準和限定軌道改進的迭代次數來保證軌道改進正常結束。采樣弧長為一圈。

圖1 解析法軌道預報10min位置速度殘差圖

圖1預報10 min三軸位置中誤差為7.46 m,均方差為9.97 m;三軸速度中誤差為0.0424 m/s,均方差為0.0435 m/s。可以看出,解析法定軌具有外推功能,在短時間內可以保證精度,從而在定位板復位的情況下可以保證定位結果的連續性和穩定性。

4 結 論

介紹了一種基于GPS定位結果的簡化解析法軌道預報方案,并且根據方案編寫了相應的程序。通過實例論證了該方案軌道預報的方法,可以保證定位板輸出數據的連續性和穩定性。源程序總長度為16 KByte,目標文件長度為30 KByte,執行文件長度為52 KByte。程序的大小滿足目前國內星載GPS接收機DSP的要求。說明了該簡化解析法算法簡單,在滿足一定的定軌精度情況下能有效降低星載軟件的復雜度,具有一定的工程實用價值。

[1]張玉詳.人造衛星測軌方法[M].北京:國防工業出版社,2007.

[2]劉 林.航天器軌道理論[M].北京:國防工業出版社,2000.

[3]謝 鋼.GPS原理與接收機設計[M].北京:電子工業出版社,2009.

[4]郗曉寧,王 威.近地航天器軌道基礎[M].國防科技大學出版社.2003.

[5]陳俊平,王解先.附加Helmert變換參數的低軌衛星約化動力學精密定軌[J].測繪學報,2008.

[6]彭恢全,繆元興.一種解析定軌方法[J].天文研究與技術-國家天文臺臺刊,2007.