水平軸風力機葉片翼型流場的數值模擬

閆海津,李 佳,胡丹梅

(上海電力學院能源與環境工程學院,上海200090)

水平軸風力機運行時,如果翼型來流的攻角較大,繞翼型的流動邊界層就會嚴重分離,因此準確獲得翼型的氣動特性對于風力機葉片設計非常重要,但是這種復雜的分離流動現象采用試驗的方法測量非常困難,而且大量的試驗將使翼型的設計周期延長和成本增加。采用CFD計算流體力學數值模擬替代試驗測定工作確定翼型的氣動特性,可以縮短設計周期和降低設計成本,已經在實際工程中得到了廣泛的應用。NACA634系列翼型是一種總體性能表現良好的翼型,在各種水平軸風力機上得到了廣泛的應用,本文將采用CFD軟件FLUENT對該系列翼型中的NACA63425進行數值模擬[2-4],得出翼型在不同攻角下的壓力分布、升力系數、阻力系數及升阻比,分析翼型的分離流動情況。

1 風力機葉片的數值模擬

1.1 基本方程

風力機葉片的運轉速度不大,翼型的繞流可以看作不可壓縮流動。數值計算模型采用二維連續性方程和二維不可壓縮N-S方程[3]。

二維連續性方程:

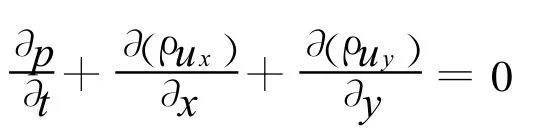
二維不可壓縮N-S方程:

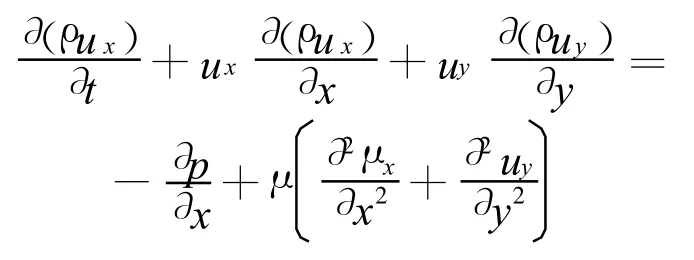
式中:ρ為空氣密度;μ為空氣的粘性系數。

1.2 網格劃分

由于所采用翼型的幾何形狀并不十分復雜,考慮到數值求解效率等因素,本文采用了C型網格。為了減少計算域外的邊界對計算過程的影響,外邊界長度分別取翼型弦長和最大厚度10倍左右的距離。為了能夠得出更加準確的結果,網格在翼型表面采取了網格局部加密方法[1],網格總數達6萬多,其中翼型表面分布節點160個。網格分布見圖1。

圖1 網格分布圖

1.3 定解條件和邊界條件

采用分離式求解器進行求解,隱式算法。模擬計算假定流場中只存在空氣單相流動,不考慮風沙、水滴等多相流的情況;空氣密度和空氣動力粘度依據模型提供的常規值并且保持為常數。因為氣流密度小計算中可以不考慮重力的影響。在求解過程中可以假定所有過程都是絕熱過程,即不考慮熱傳導與太陽輻射。本文的模擬選用RNG k-ε兩方程湍流模型,該湍流模型能夠反映各向異性和平均渦量對流動的影響,其中的湍流常數直接由重整化群理論導出并且在模型中通過一個修正項記入了平均應變率對湍流耗散率的影響,具有較高的精度和可信度[2]。方程中壓力--速度耦合采用SIMPLE算法即求解壓力耦合方程組的半隱式方法,這也是目前工程上應用最為廣泛的流場計算方法,主要用于求解不可壓縮流場的數值方法,這種方法的核心是采用“猜測-修正”的過程,在交錯網格的基礎上來計算壓力場,從而達到求解動量方程(Navier-Stokes方程)的目的[2]。方程中的動量、湍流動能均采用二階迎風格式處理。

邊界條件包括進出口邊界和壁面邊界:設定進口邊界為速度進口邊界條件,速度為無窮遠處的來流風速;考慮到計算區域相對弦長較大,流動在出口處已經得到了充分的發展,所以選用自由出流為出口邊界條件;翼型表面為無滑移固壁邊界。

2 計算結果與分析

2.1 升力系數、阻力系數及升阻比

對NACA63425翼型流場在來流攻角為0°至30°范圍下的流動情況進行的數值模擬,取來流的速度為風力機在額定工作狀態下的風速,12m/s。利用數值計算得到的翼型升力系數、阻力系數和升阻比隨來流攻角的變化結果見圖2-圖4。

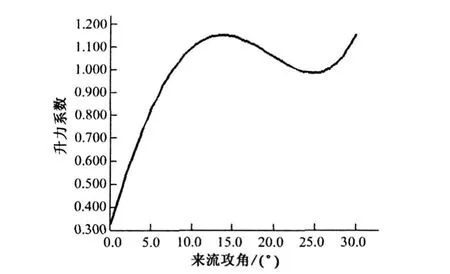
圖2 升力系數隨來流攻角的變化

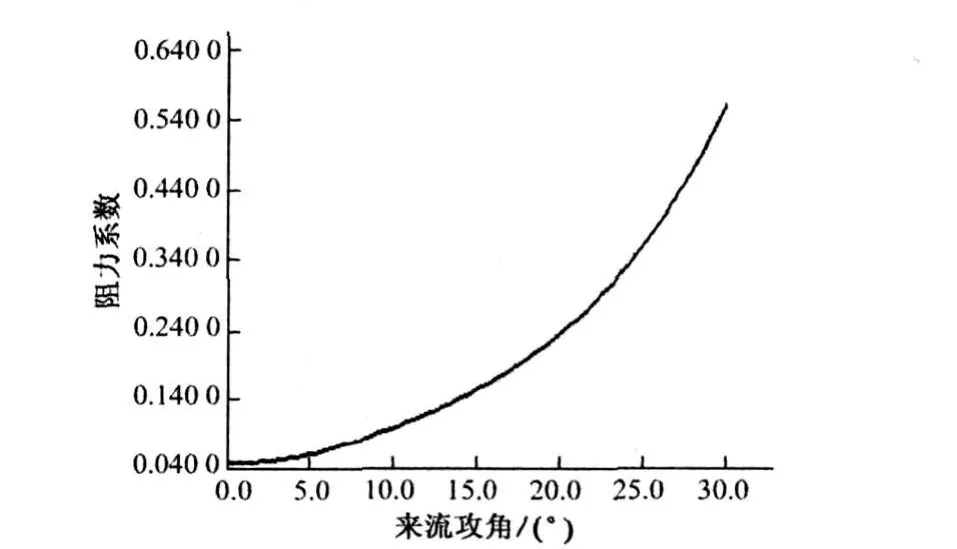
圖3 阻力系數隨來流攻角的變化

從圖中可以看到:當攻角小于12°時,翼型的升力系數和阻力系數都隨著攻角的增大而增加;攻角在12°左右時,翼型的升力系數達到最大;當攻角大于12°后,翼型的阻力系數繼續增加,但是升力系數開始下降,不過攻角增加到25°后升力系數又開始上升。這是因為隨著攻角的增加,氣流在翼型表面上的分離加劇,導致尾跡區域形成漩渦,翼型上下面壓力差和升力減小,風機進入了失速狀態。根據這些模擬計算結果可以看到,翼型NACA63425的失速攻角應該在12°附近。在實際中,風力機葉片一旦出現失速現象,風力機就會產生劇烈振動和運行不穩,為了使風力機在稍大于設計風速時仍能很好的工作,所選取的升力系數應在升力系數最大點的左側,其值最大不超過0.8～0.9倍的最大值[5]。

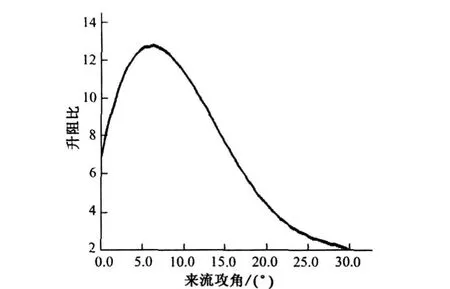
圖4 升阻比隨來流攻角的變化

翼型的升阻比反映了翼型的氣動效率,升阻比越高,翼型的氣動效率越高。由圖4可以看出,在來流攻角為7°左右時翼型的升阻比達到最高,約為l2左右。來流攻角大于7°時升阻比急劇下降,在攻角為30°時翼型的升阻比已經下降到2左右。

2.2 翼型表面的壓力分布

不同的攻角翼型表面的壓力分布的模擬計算結果見圖5-圖7。

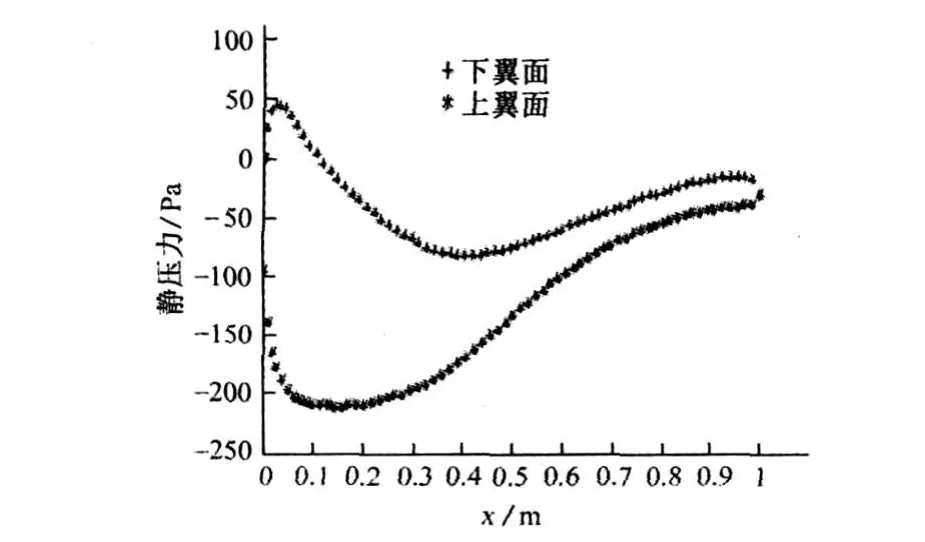
圖5 攻角為 10°時翼型表面的壓力分布

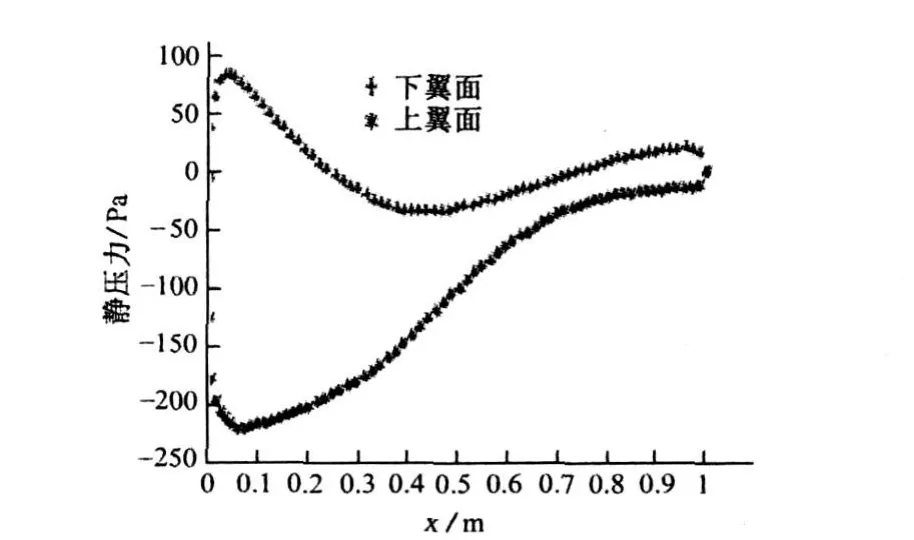
圖6 攻角為 14°時翼型表面的壓力分布

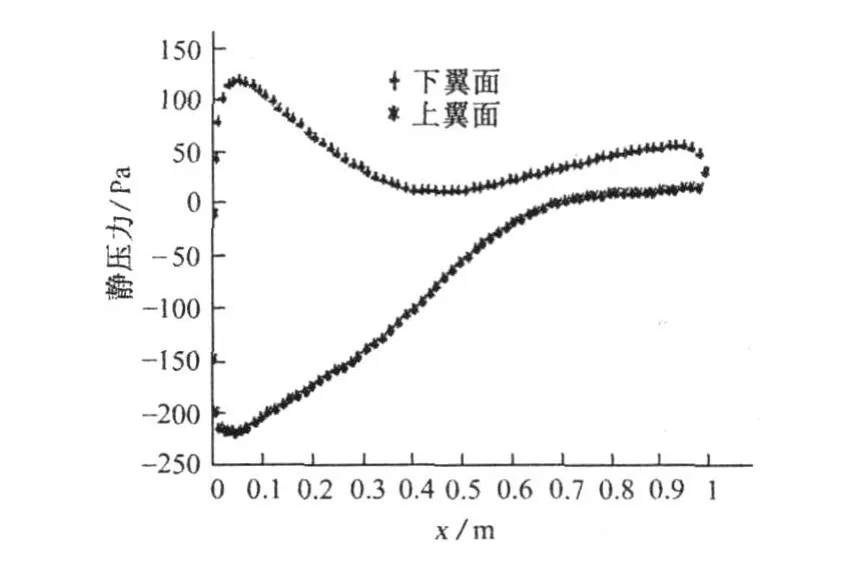
圖7 攻角為18°時翼型表面的壓力分布

對比圖5,圖6和圖7可以看出,當來流攻角為10°時翼型上下表面始終具有較大的壓差。當來流攻角增大到14°時翼型尾部上下表面的壓力差就有所減小了,隨著來流攻角的進一步增大,壓力差減小的趨勢向著翼型的前緣方向發展。對比圖6和圖7可以看出,當攻角為14°時壓差開始減小的位置大概發生在0.6弦長處,當攻角為18°時壓差減小的點已經向翼型前緣移動到弦長的0.5處左右了。造成這種現象的主要原因其實也是翼型表面的流動分離隨著攻角的增大而加劇,并且有向著翼型前緣方向發展的趨勢。

2.3 翼型流場的流線分布

不同攻角時翼型流場的流線分布模擬結果見圖8-圖10。

圖8 攻角為10°時翼型流場的流線分布

圖9 攻角為14°時翼型流場的流線分布

圖10 攻角為18°時翼型流場的流線分布

由圖8可得出,當來流攻角小于10°時,翼型繞流為附著流,未出現漩渦分離的現象;此時的翼型表面壓力分布圖也呈現出較大的壓差,即此時翼型具有較好的氣動性能,但當來流攻角增大到14°后,翼型尾部開始出現流動分離形成了漩渦(見圖9)。從圖10中還可以進一步看出,隨著攻角的增大漩渦的范圍也進一步的擴大,并向翼型前緣發展[5-7];這也正是翼型升力系數變小,表面壓差減小并且減小的趨勢向前緣移動的原因。可見,翼型流場的尾跡流動分離是影響翼型氣動特性的主要原因。

3 結論

本文利用計算流體軟件FLUENT對不同攻角下翼型NACA63425流場進行了數值模擬,得出了翼型在不同攻角下的壓力分布、升力系數、阻力系數并計算得出了升阻比。本文還通過模擬結果分析了翼型的分離流動情況,得出了影響翼型氣動性能的主要原因,總結了該翼型分離流動隨攻角的變化特征,為風力機翼型的氣動特性研究提供了參考依據。

[1]Nathan Logsdon.A procedure for numerically analyzing airfoils and wing sections[D].The Faculty of the Department of M echanical&Aerospace Engineering University of Missouri-Columbia,2006.

[2]趙偉國,李仁年,李德順,等.風力機專用翼型數值模擬中湍流模型的選擇[J].西華大學學報,2007(11):61-65.

[3]陳旭,郝輝,田杰,等.水平軸風力機翼型動態失速特性的數值研究[J].太陽能學報,2003(12):735-740.

[4]楊從新,李春輝,巫發明.水平軸風力機專用翼型的數值模擬研究[J].科學技術,2008(9):4994-8994.

[5]M ENG F.CFD investigations with respect to model sensitivity for the non-rotating flow around the NREL Phase VI Blade[R].Delft University Wind Energy Research Institute,2008.

[6]李棟,李孝偉,喬志德.大迎角粘性復雜流場的數值模擬[J].空氣動力學學報,2000(6):311-315.

[7]王友進,閆超,周濤.不同厚度翼型動態失速渦運動數值研究[J].北京航空航天大學學報,2006(2):153-157.