城市軌道交通乘客上車前分布情況的統計研究

盧 鈞 董芳芳

(1.南京地鐵運營分公司,210023,南京;2.海軍指揮學院,210018,南京∥第一作者,助理工程師)

軌道交通乘客的上車行為和時間決定著列車的最小發車間隔,進而影響整個地鐵運營工作的效率。國內外許多學者都對乘客的上車行為進行了研究。文獻[1]指出了影響列車停靠時間的主要因素;文獻[2]研究乘客站臺上和車廂內的行為特性,提出了影響乘客上下車時間的因素;文獻[3]建立了分段形式的乘客上車時間數學模型,并發現乘客上車具有分隊列現象等。上述研究均只針對乘客的上車行為,而對乘客上車前的準備工作(即候車行為)有所忽略。對于乘客群體,理性的上車行為應該遵守“先下后上”的原則,這樣可保證其上車行為的高效性。大多數地鐵車站的上車引導提示(包括引導標志、站內廣播提示等)也是基于“先下后上”的原則建立的。但現階段我國乘客的上車行為并不嚴格遵守“先下后上”的原則。實際觀測發現,在列車進站到列車停車開門的這段時間內,候車乘客會向車門口聚集;當列車車門打開時,聚集在車門口等候上車的乘客群會對下車乘客形成擁堵,進而影響整個上、下車行為的效率。所以,候車乘客上車前的分布情況對乘客的上車過程產生很重要的影響。

本文以南京地鐵新街口站為樣本,運用觀測法對候車乘客的分布情況進行統計研究。

1 上車乘客分布情況統計

1.1 背景介紹

南京地鐵新街口站站臺層的地面上貼有分區域提示的乘客上、下車引導標識(如圖1～3)。每組標識分別對應一個車門。根據車站內空間分布的不同,這些引導貼標分為中間下車兩側上車(圖1)、中間下車左側上車(圖2)和中間下車右側上車(圖3)等三種。

圖1 中間下車兩側上車的引導貼標

分區域引導貼標把每個車門前的候車區域劃分為左側上客區、右側上客區和中間下客區等三個區域。對乘客上車前在不同區域內的分布情況進行計數(對于沒有左側上客區或右側上客區的車門,相應區域的計數為0),然后求得每個車門前分布于中間下客區域的乘客數和上客總人數之比θ,進而對乘客上車前的準備情況進行統計分析。

圖2 中間下車左側上車的引導貼標

圖3 中間下車右側上車的引導貼標

1.2 上車前乘客分布情況的統計分析

若臨上車前乘客平均散布于站臺上,那么θ值應該為車門前站臺面積與車門具有吸引力的站臺面積之比。南京地鐵每節車廂的車體長度約為23 m,單側擁有供乘客使用的車門5個,車門開啟凈寬度1.4 m。據此可計算出在乘客平均分布狀態下的θ值約為0.3。

筆者于2009年10月至11月間,在南京地鐵新街口站對列車到站停穩后至車門打開這段時間內乘客于地面貼標區域內的分布情況進行統計,共獲得有效乘客數據采樣1 289個,有效θ值計算60次。觀測獲得θ值隨上客總人數的變化曲線如圖4所示。

從圖4可以看出,隨著車門前上客總人數的增加,θ值變化幅度逐漸減小。θ值在不同區間內的采樣頻率分布如表1所示。

從表1可以看出,超過70%的θ值分布在0.4～0.65之間。此數據明顯高于乘客平均分布狀態下的θ值。可見在列車到站停穩后至車門打開這段時間內,乘客在站臺上的分布是不均勻的,有向車門聚集的趨勢。

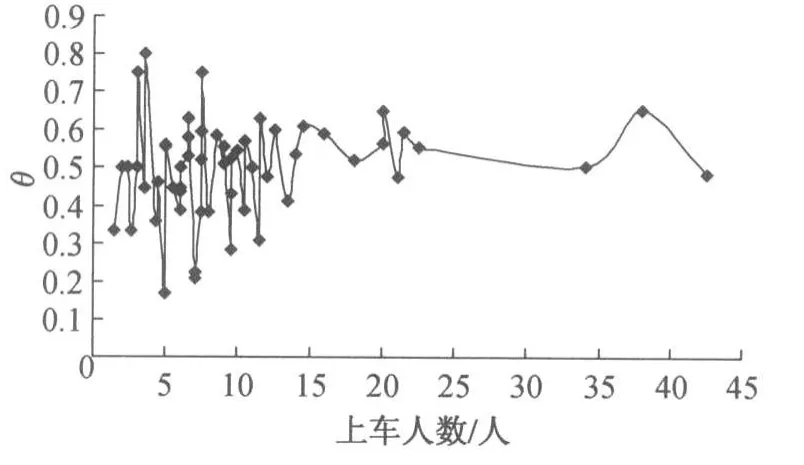
圖4 上車前乘客分布曲線圖

表1 不同區間內θ值的采樣頻率表

2 上車前乘客分布的數學模型

觀察發現,列車到站后乘客在“效率優先”的決策模型下向車門集中,形成密集人群。對于人群的分布形狀,諸學者有不同的構想。文獻[4]的研究認為,上車乘客居于車門兩側呈扇形分布;文獻[5]研究發現,對于每一個車門而言,候車乘客分布的形狀與二次函數相似,呈現出從車門向候車廳擴散的拋物線形狀。兩種模型各有利弊。兩側扇形分布的模型完全基于“先下后上”原則,車門前的乘客分布較少而車門兩側的乘客分布較多。該模型計算簡便,可方便地計算出乘客人數和人群深度之間的關系,進而對站臺設計等提供相對可靠的數據指導。但是,根據前面的研究,乘客在上車時并不會主動讓出車門前的通道,反而會聚集在車門口等待上車。所以在對候車和上車行為進行研究時,本文選用人群分布的二次函數模型進行擬合,并驗證其與實際情況的符合性。

假設乘客候車時平均分布于站臺上,則每個車門會對站臺上一個矩形區域內(見圖5)的乘客具有吸引力。這個矩形區域 ABCD的寬度和長度為:

式中:

lAB——每個車門吸引的候車乘客群的長度;

lBC——每個車門吸引的候車乘客群的深度;

l1——車廂長度;

l2——站臺寬度;

n——每節車廂車門個數。

列車到站后,車門即將打開時矩形ABCD內的候車乘客匯聚到拋物線ABcd所構成的區域內等候上車。以車門中心點為原點,車門為橫坐標軸(x軸,指向車頭方向為坐標軸正方向),車門的中軸線為縱坐標軸(y軸,指向站臺中心方向為坐標軸正方向),建立如圖5所示的直角坐標系。乘客群分布形狀的二次曲線(即拋物線ABcd)方程為:

式中:

ldc——車門寬度。

則拋物線ABcd的方程為:

列車到站后,乘客即自動集結到車門口等候上車。這時乘客群從矩形ABCD內集中至拋物線ABcd內,人群深度也由lBC降低到l fc,即上車人群集結于拋物線ghcod內。由于此時人群密集,可認為上車乘客均勻分部于拋物線 ghcod區域內,那么,站在下車地標上的乘客數與所有乘客數之比θ就等于相應區域的投影面積之比。即:

圖5 上車人群二次函數模型示意圖

3 模型參數擬合

南京地鐵新街口站站臺寬約14 m。故:l1=23代入式(1)、(2)、(6),求得乘客在臨上車前短暫時間內分布形狀的二次函數曲線為:y=1.458(x2-0.49)。

觀察發現,上客總人數超過5人時,隨總人數的增加,上車乘客群分布形狀的面積變化不大,這時靜態人群密度(ρ)隨總人數(m)的變化近似呈線性關系。本次試驗中,總人數為43人時,靜態人群密度約為6人/m2;總人數為5人時,靜態人群密度約為1人/m2。據此得到總人數超過5人時人群密度隨總人數變化的線性方程為:ρ=0.133m+0.333。

把試驗中θ值在0.4～0.65之間的所有樣本實測值與二次函數模型計算得到的擬合值進行對比分析,如表2及圖6所示。

結合圖6、表2可以看出,車門前總人數超過5人時,實測值曲線沿模型擬合值曲線上下波動;除少量實測點外,其余實測點相對誤差的絕對值均低于10%。可見模型總體上反映了人群分布隨總人數增長的變化趨勢。但是偏離模型曲線的實測數據的存在表明人群分布狀態還受到其他因素的影響。從圖6擬合曲線的趨勢來看,當車門口總人數偏少時,超過半數的乘客會選擇直接在車門口等待上車;隨著總人數的增多,選擇直接在車門口等待上車的乘客數與總乘客數的比趨近于0.5。

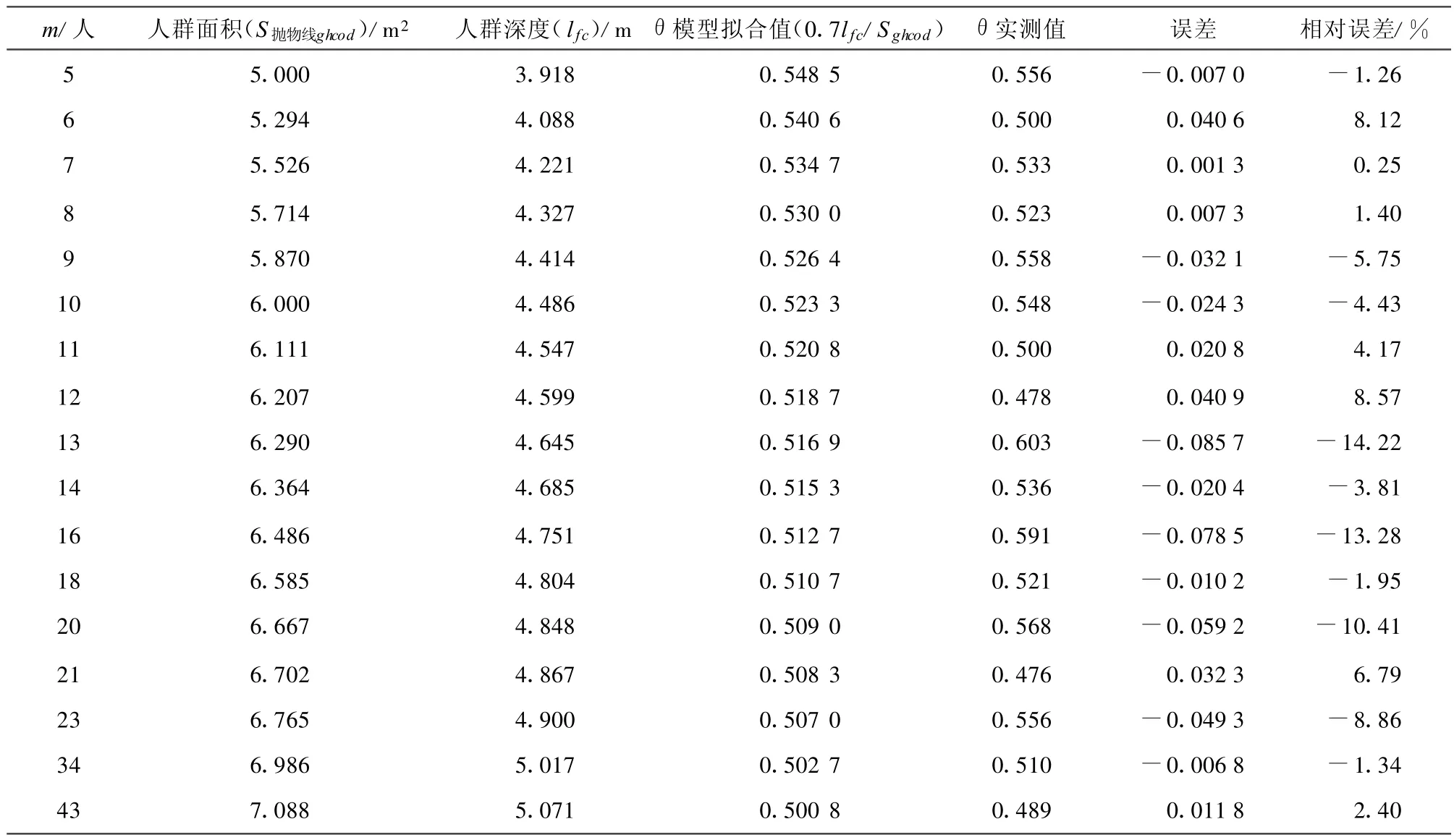
表2 乘客分布模型擬合值與實測值的部分數據對比表

圖6 實測乘客分布數據與模型擬合值對比圖

4 結語

本文基于對南京地鐵新街口站站臺層乘客候車、上車分布形態的實際觀測,分析了城市軌道交通乘客上車前在車門口聚集等待上車時的分布特性。根據對乘客上車行為的觀測研究,引入θ值的概念直觀地反映乘客在車門口的聚集情況,并且建立了上車時乘客分布的二次函數模型。實際算例表明,該模型能較好地反映乘客分布隨總人數增長的變化趨勢。

模型中僅引入了不同方位上車的人數作為影響乘客分布的主要因素。實際上影響乘客分布的因素還有很多,如站臺引導服務水平、列車停靠狀況等。這方面的研究可對本模型進行進一步修正。

[1]Kraft W H.An Analysis of the Passenger Vehicle Interface of Street Transit Sy stem with Application to Decision Optimization[D].New Jersey:New Jersey Institute of Technology,1975.

[2]Pead M.The Impact of Boarding and Alighting Passengers on the Dwell Time at Railway Stations[D].Birmingham:A ston University,2007.

[3]曹守華,袁振洲,趙丹.城市軌道交通乘客上車時間特性分析及建模[J].鐵道學報,2009,31(3):89.

[4]沈景炎.乘客動態分布與站臺寬度的研究[J].城市軌道交通研究,2001,4(1):21.

[5]徐尉南,吳正.地鐵候車亭客流運動的數學模型[J].鐵道科學與工程學報,2005,2(2):73.

[6]李三兵,陳峰,李程壘.對地鐵站臺集散區客流密度與行進速度的關系探討[J].城市軌道交通研究,2009(12):34.