預測飛行路徑透視顯示方法研究

程建鋒， 董新民， 薛建平

(空軍工程大學工程學院，西安 710038)

0 引言

在飛行員操縱指令信號顯示方法中，傳統的顯示器僅僅提供了相對于飛機當前狀態的二維平面信息，駕駛員要通過這些信息重構飛機的時空情景，增加了負擔［1］。而帶有預測器的透視飛行路徑顯示不僅以隧道的形式提供給飛行員指令信息，而且還以三維的形式提供給飛行員預測位置信息，飛行員只需在一個接近真實情景中控制飛機沿隧道中心飛行，即可完成對航跡的控制，從而大大減輕了駕駛員的負擔。

預測飛行路徑顯示有多種算法，文獻［2］中給出了“圓形預測算法”和“全圍預測算法”，文獻［3］應用這些算法設計了橫側向預測顯示器，文獻［4］基于人工控制理論從駕駛員角度進行了分析，文獻［5］對縱向和橫側向通道預測顯示器進行了初步的設計。但是，目前對該問題的研究主要集中在橫側向通道方面，而將預測顯示算法應用于縱向通道還不多見。文中將傳統的基于圓形路徑預測的顯示方法應用于縱向通道的設計。首先，應用人工控制理論對其特性進行分析，指出其品質缺點;其次，采用基于q反饋的“非圓形預測”算法改進了傳統的算法，最后通過理論分析和仿真驗證其有效性。

1 帶預測器的路徑顯示與補償控制

帶預測器的飛行路徑顯示方法提供給駕駛員飛機基于當前狀態預測的位置信息和指令路徑信息，如圖1 所示［6］。

圖1 帶預測器的透視飛行路徑顯示圖Fig.1 Perspective flight-path predictor display map

其中，預測器顯示的是根據飛機當前的姿態、速度、加速度等參數預測的未來TPR時刻后飛機的位置，指令飛行路徑是以“隧道”的形式顯示的。預測器與對應預測時刻的“隧道”的交叉部分提供了預測位置偏差信息［7－8］。駕駛員利用這些偏差信息，采取“補償控制”的方式操縱飛機使其沿隧道中心飛行。“補償控制”是人工控制的一種重要方式，人工控制理論指出:為了兼顧系統的操縱特性和減輕駕駛員負擔的雙重要求，控制系統(駕駛員除外)在穿越頻率附近應具有如下所述的特性［9］，YPR(s)YC(s)近似為一個積分環節，即:

式中:YPR(s)為預測器傳遞函數;YC(s)為飛機模型。并且積分特性在穿越頻率附近要有足夠的帶寬，同時還需要考慮以下因素:人機系統的穩定性、對擾動的靈敏性等。

2 基于圓形飛行路徑預測的顯示方法

預測器提供了飛機TPR時刻后的位置信息，文中采用“圓形預測法”，應用二階泰勒展開式，TPR時刻后的飛機縱向的位置為［1］

假設預測時間很短，飛機速度V為常數，航跡角滿足式(3):

其中:TPR為預測時間。上式可表示為圖2。

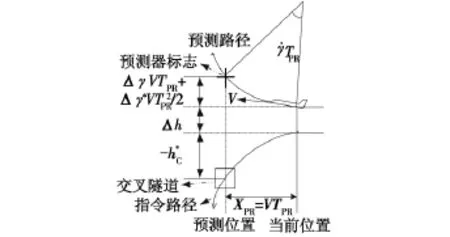
圖2 “圓形預測法”原理圖Fig.2 Principle of the circular flight-path predictor

根據控制理論，可以把未來時刻的偏離用當前時刻飛機的運動來表示，如圖3所示。

圖3 圓形飛行路徑預測顯示原理方框圖Fig.3 Block diagram of the circular flight-path predictor

結合圖3，式(2)的Laplace變換為

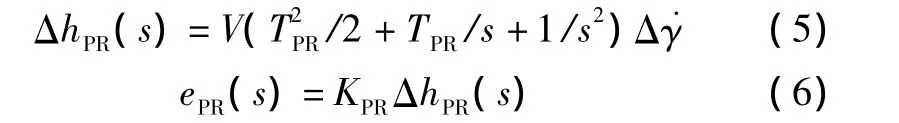
式中:ePR為顯示誤差;KPR為顯示增益。聯合式(5)和式(6):

式(7)的分子多項式可化為

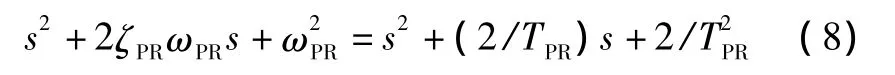
式中:ωPR=/TPR;ζPR=1/

假設飛機的模型為

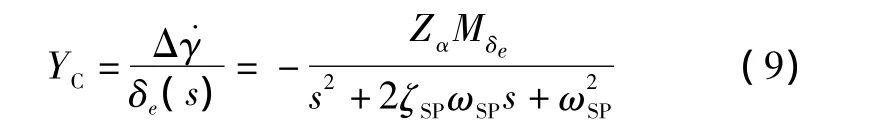
因此:

系統的Bode圖如圖4所示。

由圖可見，系統在穿越頻率處的響應近似為一個比例環節，不能夠完全滿足人工控制的相關要求。同時，由于反饋中引入了相對于˙γ的較大的反饋量/2，也導致了它對擾動的靈敏度大。

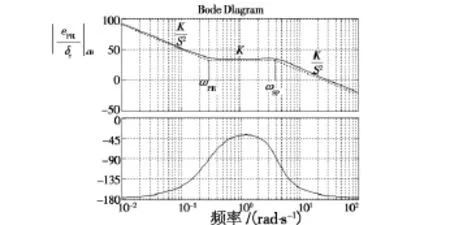
圖4 圓形預測法預測器－飛機系統Bode圖Fig.4 Bode plot for predictor-aircraft system with CPFP display method

3 基于q反饋的路徑預測顯示方法

為了克服以上缺點，用q反饋代替原來的˙γ反饋，如圖5所示。

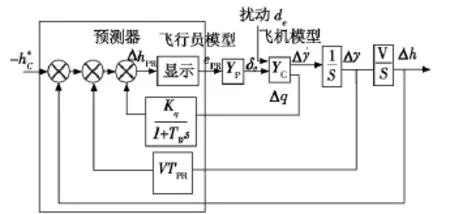
圖5 基于q反饋飛行路徑預測顯示原理方框圖Fig.5 Block diagram for predictor-aircraft system based on q-feedback theory

根據圖5:

根據飛機間的變量關系為

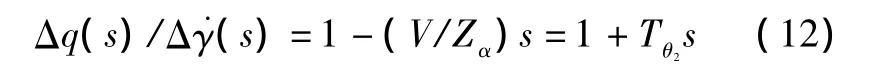
把式(13)代入式(12):

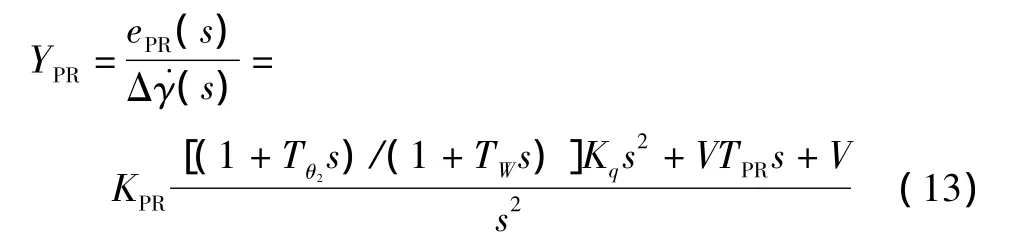
取 TW=Tθ2，式(14)可簡寫為

分析式(14)可以得出，通過調整Kq和TPR，可以使YPR(s)擁有兩個實根，而非一對共軛復根，從而可以使系統滿足人工控制理論相關要求。

為了滿足上述要求:假設式(14)的分子為

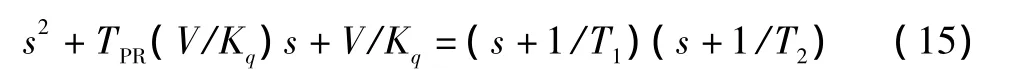
所以:

下面將依據式(16)對改進型系統的特性分析如下。

1)K/s要求。通過調整不同的T1，T2即可滿足。

2)穿越頻率出積分段帶寬要求。為了保證積分段有足夠的帶寬，假設:T2＜＜T1，

所以:

根據上面分析，式(16)示意Bode圖如圖6所示。

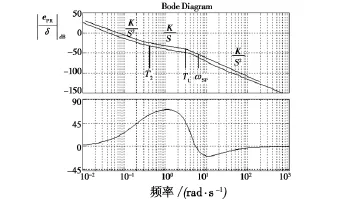
圖6 q反饋法系統示意Bode圖Fig.6 Bode plot for predictor-aircraft system based on q-feedback

通過分析可得:在T2和T1之間可以產生積分特性，并且可以使T1接近ωSP，從而保證系統有足夠的帶寬。而這些要求都是通過合理選擇Kq和TPR來滿足的。根據式(17)確定:

3)抗干擾性分析。q反饋飛行路徑預測器比基本預測器的抗干擾性大大增強，因為，與前者相比，q反饋中最易受影響的變量的系數Kq大大減小了，從圖3和式(18)可以看出:

取 TPR=5 s，ωSP＞2 rad/s，則:

所以，采用q反饋大大降低了干擾對系統的影響。并且，當 ω ＞1/Tθ2時，q反饋型的1/1+TWs也會明顯起作用，降低干擾的影響。

4 仿真分析

選取飛行狀態V=240 m/s，H=10 000 m，飛機短周期方程為［10］

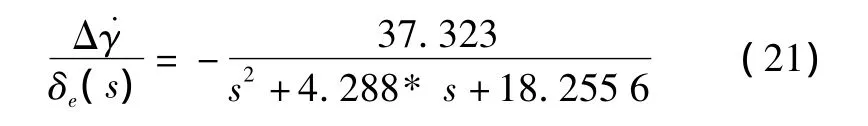
駕駛員模型取經典的McRuer模型［11］:

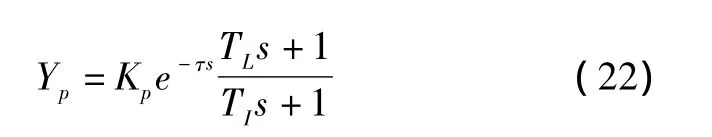
其中:Kp是駕駛員等效增益，取為1;τ為駕駛員反應延遲，取為0.2;TL和TI分別為超前和滯后補償的時間常數，分別為 0.3 s和 0.5 s。

風的模型假設為一個隨機擾動。

預測時間TPR=5 s，飛行路徑顯示器的任務是指引飛行員下降500 m，分別按照圖3和圖5進行仿真，結果見圖7，圖8。

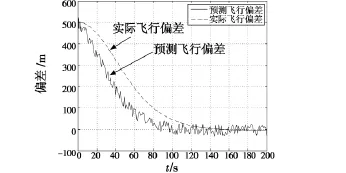
圖7 圓形飛行路徑預測顯示仿真圖Fig.7 Simulation results of CPFP display method

圖8 q反饋飛行路徑預測顯示仿真圖Fig.8 Simulation results of q-feedback-based display method

從圖中可以看出，預測飛行偏差比實際飛行偏差超前一段時間，體現了預測器的作用;相比于傳統的顯示方法，改進型顯示方法能夠大大降低擾動對顯示的影響。

5 結論

對比以上兩種方法，基于圓型預測顯示方法的物理意義明確，它是假設在預測的TPR時間段內飛機保持當前時刻的曲率飛行，而q反饋實質上是一個“非圓形預測法則”，它用較小曲率Kq代替了較大的曲率Kγ。但是，它又比較符合實際，因為在TPR時間段內(通常為5～7 s)，駕駛員會不斷地操縱飛機來減小誤差。從而減小了飛行軌跡曲率，可以看出，q反饋實質上在理論位置與實際位置之間進行了折中，同時，采用q反饋，物理上也比˙γ反饋容易實現。

通過以上分析，采用q反饋有效地克服了縱向圓形預測顯示方法的缺陷，改善了人機閉環系統的性能。

［1］張德斌，郭定，馬利東，等.戰斗機座艙顯示的發展需求［J］.電光與控制，2004，11(1):53-55.

［2］GRUNWALD A J.Predictor law for pictorial flight displays［J］.Journal of Guidance Control and Dynamics，1985，8(5):545-552.

［3］SACHS G.Improved predictor control law for tunnel display［R］.AIAA:2006-6220，2006.

［4］SENNES U.Perspective flight path and predictor display with two-axis control coordination［R］.AIAA:2000-4450，2000.

［5］SACHS G.Perspective predictor flight-path display with minimum pilot［J］.Journal of Guidance Control and Dynamics，2000，23(3):400-429.

［6］SWEET B T.Modeling of perception and control of attitude with perspective displays［R］.AIAA:2005-5891，2005.

［7］STURHAN I.Predictor-tunnel display with audio-visual aids for improving flight path control［R］.AIAA:2007-6420，2007.

［8］LAN T M，MULDER M，van PAASSEN M M.Comparison between augmentation techniques for tunnel-in-the-sky displays［R］.AIAA:2004-5238，2004.

［9］高金源，李陸豫，馮亞昌.飛機飛行品質［M］.北京:國防工業出版社，2003.

［10］魯道夫.飛行控制［M］.肖業倫，譯.北京:國防工業出版社，1999.

［11］袁修干，莊達民，張興娟.人機工程計算機仿真［M］.北京:北京航空航天大學出版社，2004.