異步電機反饋線性化解耦控制

郭春平，王 奔，趙岳恒，李 泰

(西南交通大學 電氣工程學院，成都 610031)

1 引言

實現異步電機高性能控制的關鍵是對其時變參數的準確識別和獲得轉速、磁鏈兩個子系統間的完全解耦[1]。自20世紀提出的基于磁場定向矢量控制技術以來，出現了很多有效的解耦控制方法[2-4]，進一步提高了異步電機系統的調速性能。

近20年來，基于反饋線性化思想的非線性控制理論在電機調速系統中得到了大量的研究，通過坐標變換和狀態反饋，可以對異步電機磁鏈和轉速實現完全線性化解耦控制。參考文獻[5]和[6]討論了應用微分幾何理論，通過多輸入、多輸出非線性狀態反饋對電機轉子轉速和轉子磁鏈進行線性化解耦控制，但是這一方法實現的異步電機調速系統的動靜態性能不是很好，不容易按照預先所期望的性能指標去任意設計。為解決這一問題，筆者提出將線性系統狀態反饋極點配置理論運用于已反饋線性化的異步電機轉子轉速控制器和磁鏈控制器設計中，以提高整個系統的動靜態性能，滿足預先所期望的要求。仿真研究表明，這種處理方案達到了期望效果，證實了該方案在理論上的正確性，并具有可行性。

2 異步電機非線性狀態反饋精確線性化模型

2.1 異步電機放射非線性模型

在兩相靜止坐標系(即α-β坐標系)下，以轉子電角速度、轉子磁鏈和定子電流作為狀態變量的異步電機五階狀態方程為：

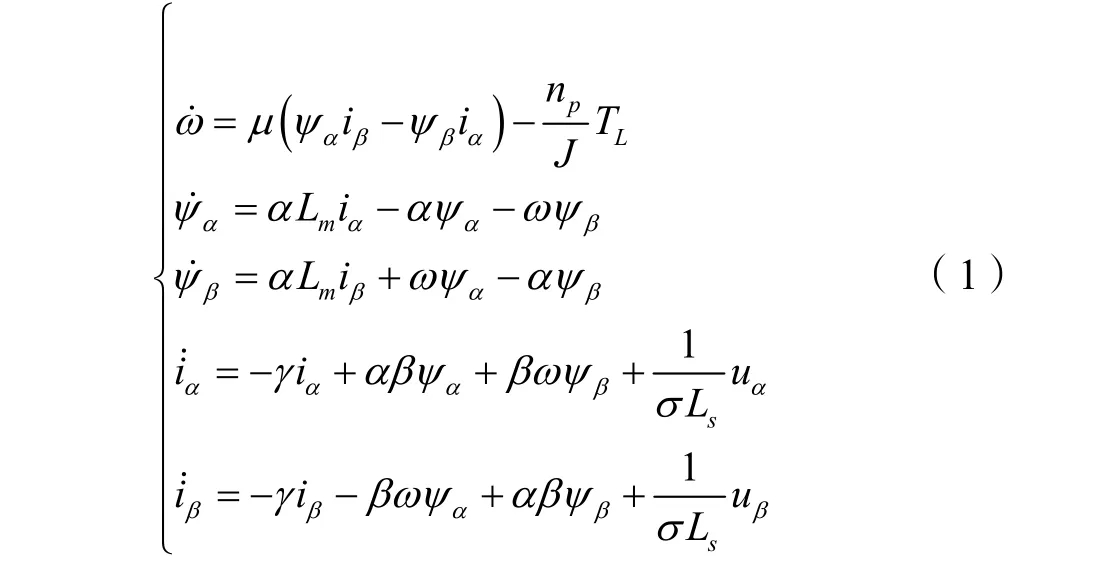
輸出方程為：

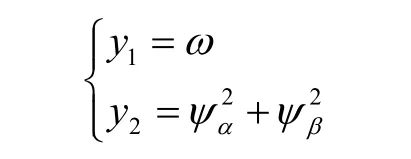
把方程(1)寫成仿射非線性方程形式，則為：

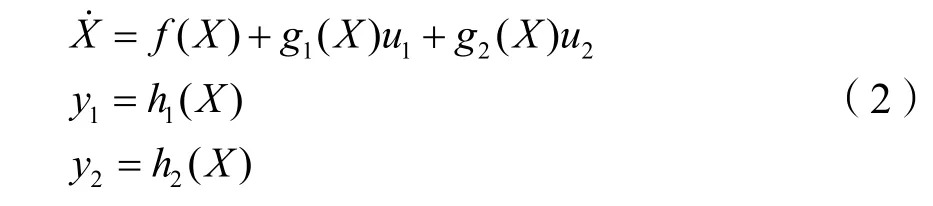
其中：

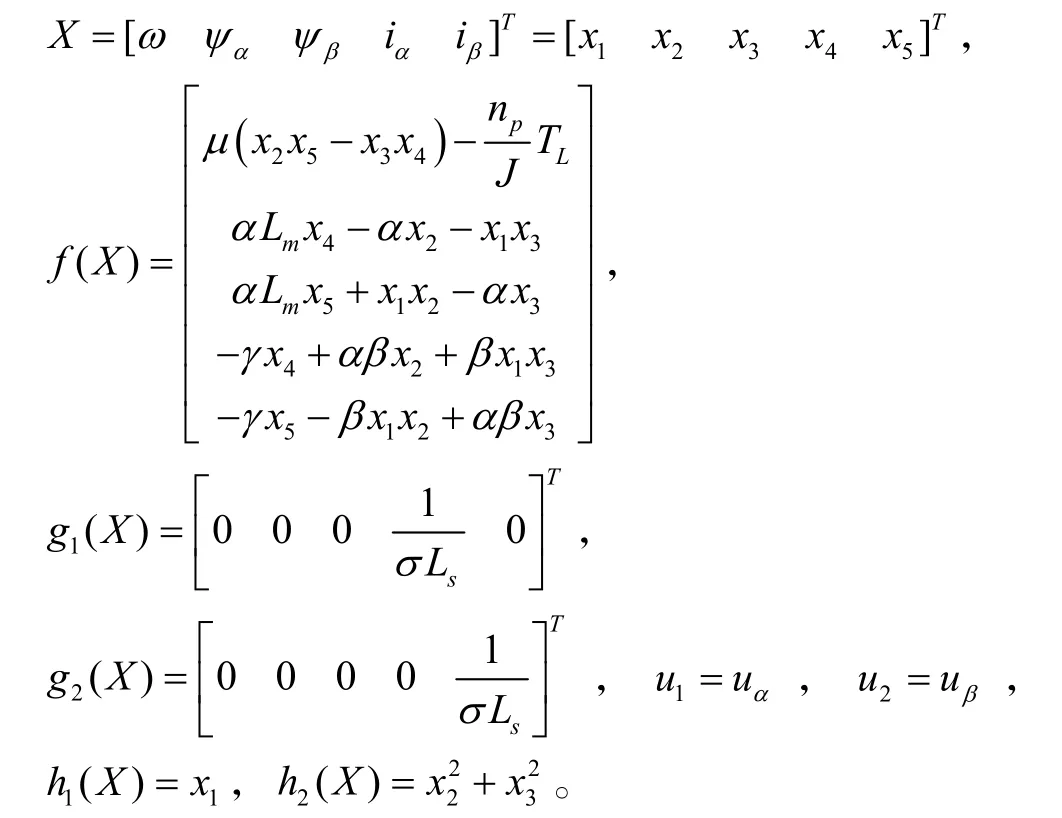
2.2 坐標變換

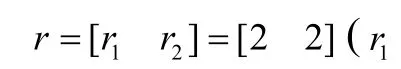
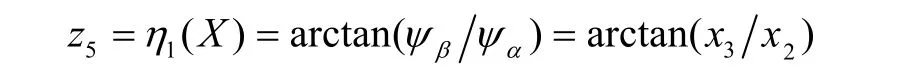
根據非線性系統微分幾何線性化方法，可得原系統線性化的坐標變換 Z =Φ(X )為：

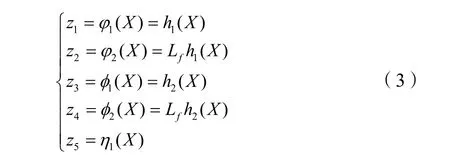
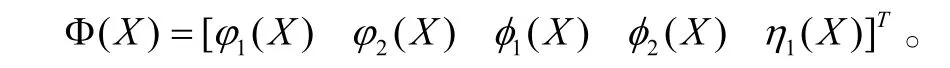
在坐標變換（3）關系下，系統（2）的狀態方程可轉化成如下形式：

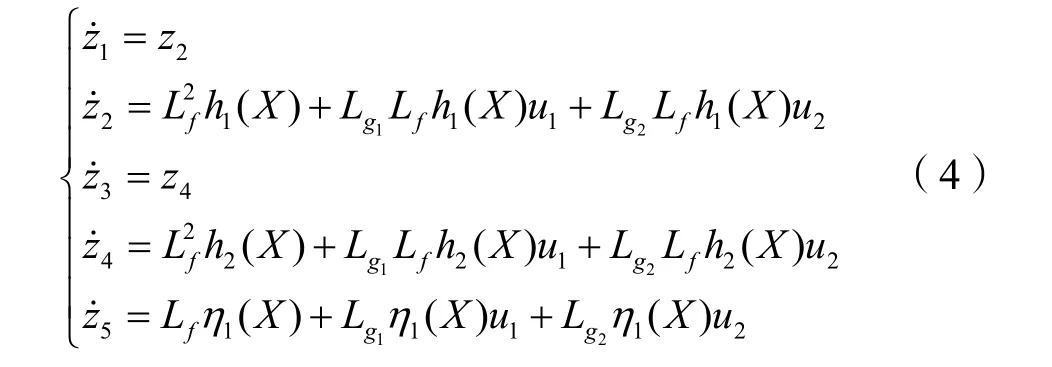
2.3 狀態反饋控制律

由式（4）中第2、第4兩個方程可得

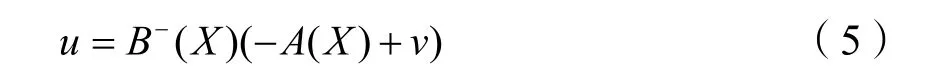
式（5）中，v為異步電機反饋線性化后的“虛擬輸入量”，引入狀態反饋就可以求出原系統（2）的實際控制律u。其中：

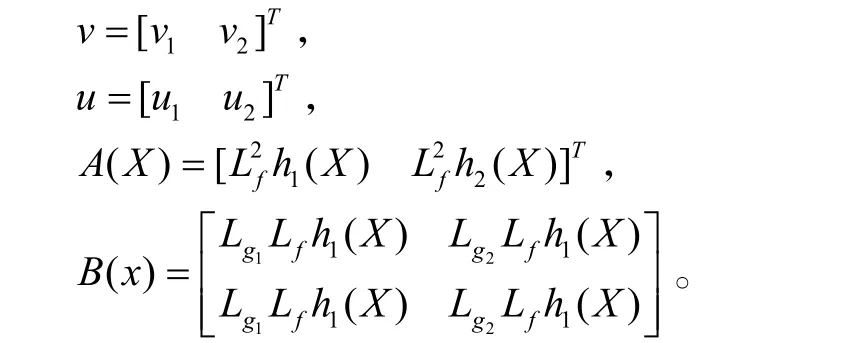
異步電機非線性狀態反饋線性化后的整個系統方程為：

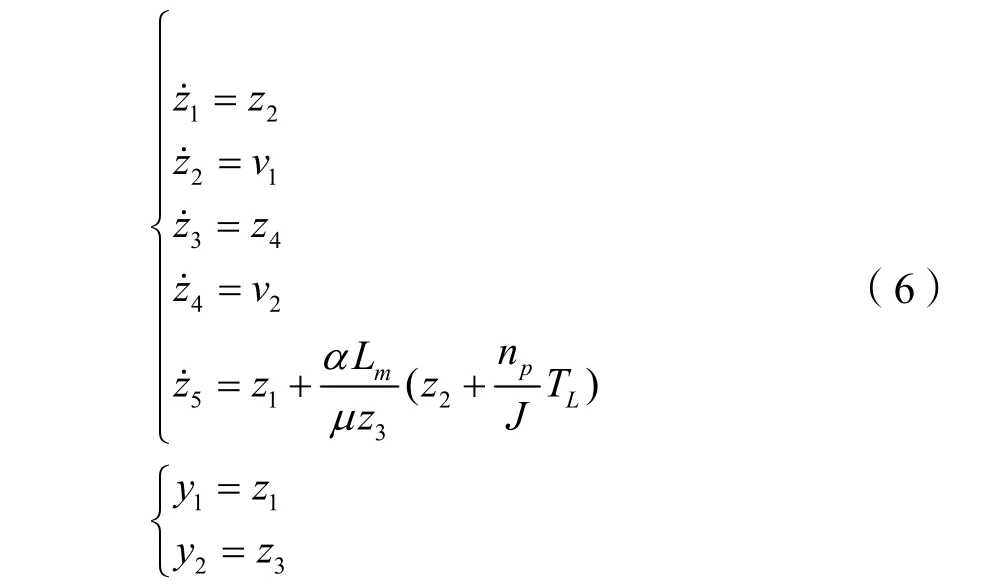
2.4 零動態穩定性問題

要使上述線性化方法有效，還必須對系統（6）中最后一個零動態方程：

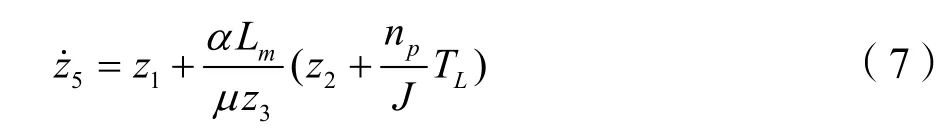
驗證其穩定性：只有該零動態方程是穩定的，才可以保證整個系統（6）是穩定的，亦即才能夠說明上述線性化方法是有效的。

由于異步電機調速系統就是要控制這兩個輸出，使電機轉速和磁鏈幅值跟蹤給定值，即期望：

在迫使系統（6）達到平衡點，即滿足式（8）的情況下，系統（6）中的z1、z2、z3和z4均為系統在平衡狀態工作點時的值，這樣式（7）可得：

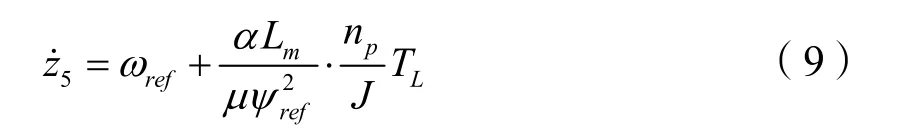
[5]中對該零動態方程穩定性對該問題有較詳細的定性分析，也驗證了上述線性化方法是有效的。在分析零動態穩定性問題時，當零動態方程比較復雜，不能夠通過常規數學方法來定量分析時，可以通過數值分析的方法來進行定量分析驗證。對方程(9)的穩定性問題，運用數值分析的方法來進行定量分析時，容易驗證該方程也是穩定的，詳細的分析過程在此不作具體的展開論述。

3 轉速控制器和磁鏈控制器設計

下面運用輸入變換-極點配置理論[9,10]，為線性化后的系統（6）設計其轉速控制器和轉子磁鏈控制器。由于反饋線性化后的系統轉速子系統和轉子磁鏈子系統具有相同的結構，為了簡化分析設計過程，這里僅對轉速子系統控制器進行設計，轉子磁鏈子系統控制器設計過程與其完全相同。

為了敘述上的簡化，將轉速子系統從反饋線性化后的系統（6）中抽取出來，寫成狀態方程的形式，可得

其中，

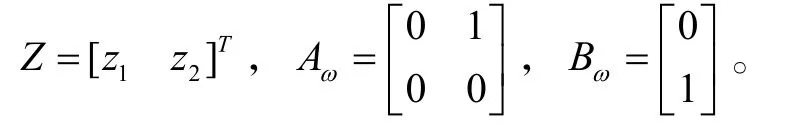
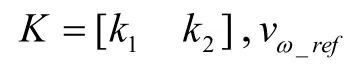
假定對轉子子系統（10）的動靜態性能指標有如下要求：輸出超調量σ≤5%；峰值時間 tp≤ 0 .1s；靜態位置誤差 ep=0。根據二階系統性能指標時域計算公式，可得

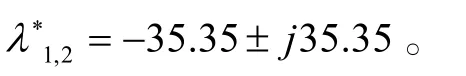
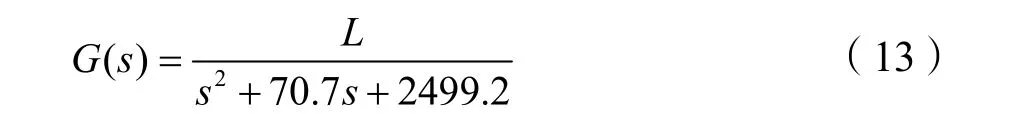
系統要求靜態位置誤差 ep= 0 ，于是有

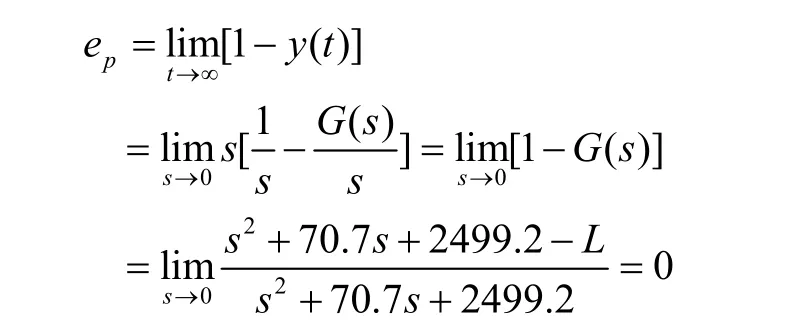
由此可得 L = 2 499.2。綜合式（11）～（13），有

異步電機整個調速系統的結構控制框圖，如圖1所示。

4 仿真研究

為了驗證異步電機狀態反饋線性化與狀態反饋極點配置控制方案的正確性，在一臺籠型異步電機上進行了仿真。電機參數：額定功率 PN= 3 5kW ，額定電壓 UN= 3 80V，額定頻率 fN= 5 0Hz ，額定轉矩TL= 200N? m ， Rs= 0 .4Ω ， Rr= 0 .5Ω ， Ls= 0 .09H ，Lr=0.09H，Lm=0.08H，np= 2 ， J = 0 .09kg? m2。

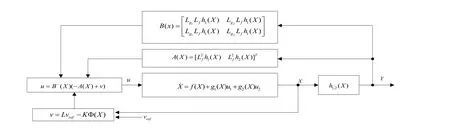
圖1 異步電機狀態反饋控制系統框圖

由于本異步電機調速系統設計方案中用到異步電機的轉子磁鏈，所以在對上述控制方案進行仿真驗證時，轉子磁鏈可以通過式（14）進行觀測求解[4]。

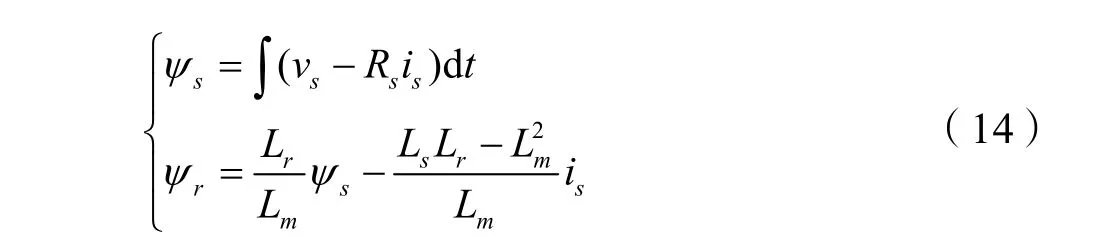
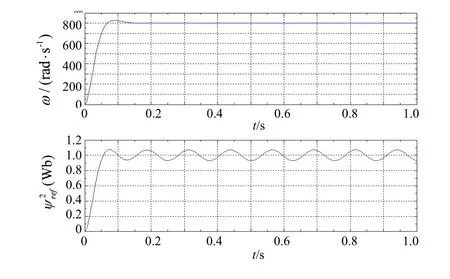
圖2 轉速和磁鏈子系統解耦仿真驗證

從仿真結果可以看到，當給定磁鏈幅值受到干擾時，電機轉速沒有發生變化，實現了轉速和磁鏈的完全解耦控制，而基于磁場定向的矢量控制系統很難實現這一點。圖3給出了整個系統在給定輸入、不存在干擾情況下系統仿真結果。

可見，通過對反饋線性化后的系統，應用狀態反饋極點配置方法來進行求解，整個系統具有很好的動靜態性能，到達了期望結果。

以上仿真結果說明，狀態反饋線性化和狀態反饋極點配置理論，在異步電機調速系統中的應用是正確的，具有可行性。

5 結語

仿真研究驗證了，應用微分幾何和線性系統極點配置理論可以將強耦合非線性的異步電機系統實現輸入、輸出線性化解耦控制，所設計的磁鏈控制器和轉速控制器能夠很好地保證系統具有良好的動靜態性能，達到了預先設計時的期望目標。本控制方案思路清晰，結構簡單，具有較好的理論研究價值與工程應用前景。

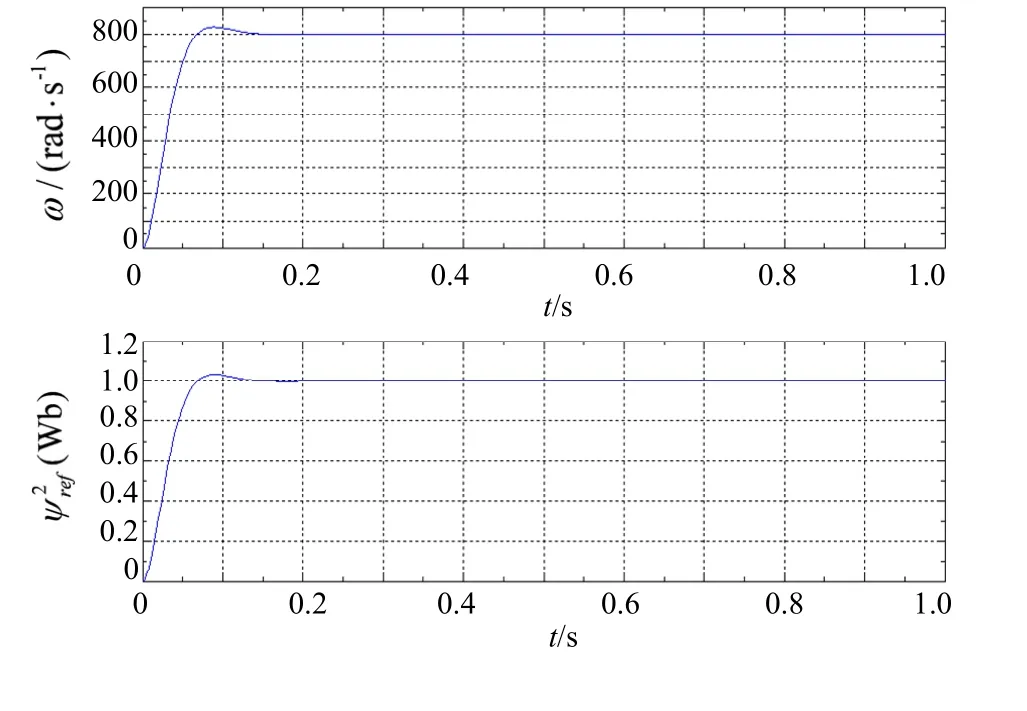
圖3 轉速和磁鏈子系統動靜態性能仿真驗證

[參 考 文 獻]

[1]孫東升. 基于線性化反饋的異步電動機自適應解耦控制[J]. 電機與控制應用, 2006, 12(3): 7-11.

[2]Peter Vas. Sensorless vector and direct torque control[M]. New York: Oxford University Press,1998.

[3]Cristian Lascu, Ion-Boldea, Frede-Blaabjerg.Very-low-speed variable structure control of sensorless induciton machine drives without signal injection[J]. IEEE Transation on Industry Application, 2005,42(2):591-598.

[4]郭春平, 王奔, 李泰, 等. 一種改進型異步電機直接轉矩控制系統研究[J]. 電氣傳動, 2008, 38(7):17-21.

[5]張春朋, 林飛, 宋文超, 等. 基于直接反饋線性化的異步電動機非線性控制[J]. 中國電機工程學報,2003, 23(2): 99-107.

[6]孟昭軍, 孫昌志, 安躍軍, 等. 狀態反饋精確線性化永磁同步電動機轉速控制[J]. 電機與控制學報,2007, 11(1): 21-28.

[7]盧強, 孫元章. 電力系統非線性控制[M]. 科學出版社, 1993.

[8]AIBERTO. Nonlinear Control System (3thedition)[M]. Springer Verlag Limited, 1995.

[9]鄭大鐘. 線性系統理論(第二版)[M]. 北京: 清華大學出版社, 2002.

[10]長管. 現代控制理論[M]. 哈爾濱: 哈爾濱工業大學出版社, 1997.