利用GPS觀測資料解算地球自轉參數

何戰科，楊旭海，李志剛，程宗頤

?

利用GPS觀測資料解算地球自轉參數

何戰科1,2，楊旭海1，李志剛1，程宗頤3

（1. 中國科學院國家授時中心，西安 710600； 2. 中國科學院研究生院，北京 100039； 3. 中國科學院上海天文臺，上海 200030）

利用22個IGS（International GNSS Service）跟蹤站（IGS05）的連續觀測資料估算地球自轉參數ERP( Earth rotation parameters)（地球自轉參數在測繪和衛星導航中是一組關鍵的參數），并與IGS地球定向參數 EOP（Earth orientation parameters）（UTC 12:00:00）和IERS（International Earth Rotation Service）C04（UTC 00:00:00）同時刻的結果相比較。比較結果表明：與IGS EOP比較，極移在方向差值的RMS 為0.0214 mas，極移在方向差值的RMS 為0.0662 mas，1-差值的RMS 為0.0260ms；與IERS C04比較，極移在方向差值的RMS為0.0203 mas，極移在方向差值的RMS為0.0354 mas，1-差值的RMS為0.0016 ms。以上差別均在IERS C04精度范圍之內，我們解算的地球自轉參數結果是可信的。

地球自轉參數；全球定位系統（GPS）；國際GNSS服務組織（IGS）；國際地球自轉服務組織（IERS）

地球自轉參數（ERP）是指極移（polar motion）和日長變化（LOD），這些參數決定著地面觀測站在空間的精確位置以及地球坐標系在空間的指向。它與歲差、章動一起構成地球定向參數（Earth orientation parameters，簡寫為EOP），它是實現天球參考架與地球參考架相互轉換的參數。人造衛星和宇宙飛行器的精密定軌[1]和導航都需要高精度的地球自轉參數，因此，對地球自轉參數的研究具有重大的意義。

隨著全球定位系統（GPS）、激光衛星測距（SLR）、甚長基線干涉測量（VLBI）、激光測月（LLR）和星基多普勒無線電定軌定位系統（DORIS）等現代空間技術的發展，定位精度得到大大提高，從而使得高精度實時測定地球自轉參數成為可能。目前國際地球自轉服務組織（International Earth Rotation Service，簡寫為IERS）利用全球LLR、SLR、VLBI、DORIS和GPS網，測定地球自轉參數的精度已達亞厘米級[2]。但SLR、VLBI等技術設備龐大，難以普及和流動，以及觀測數據量少，因此IERS目前每天給出1個EOP解。顯然這些觀測遠不能滿足地球自轉參數高分辨率的需要。

隨著IGS（International GNSS Service）跟蹤網臺站數的不斷增加、GPS觀測資料質量的提高和GPS數據處理技術的改進[3-5]，GPS觀測資料已經可以用來加密解算地球自轉參數。1992年起IGS組織全球聯測并成功求解EOP，1995年起IERS正式采用GPS與VLBI等技術聯合求解EOP。利用GPS觀測資料建立我國獨立解算地球自轉參數的系統，對于我國守時、授時、COMPASS導航系統的定位、人造衛星精密測定軌和深空探測等科研工作都具有重要意義。

1 解算原理

在高精度GPS定位中，GPS載波相位觀測值可以抽象地表示為初始時刻的軌道根數、攝動參數、測站坐標、地球自轉參數、大氣延遲參數和相位模糊度等待估參數的函數[6-8]：

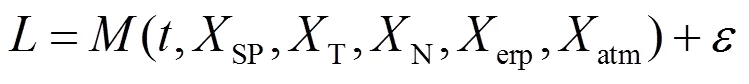
式（1）是非線性函數，求解待估參數時要求將其線性化為

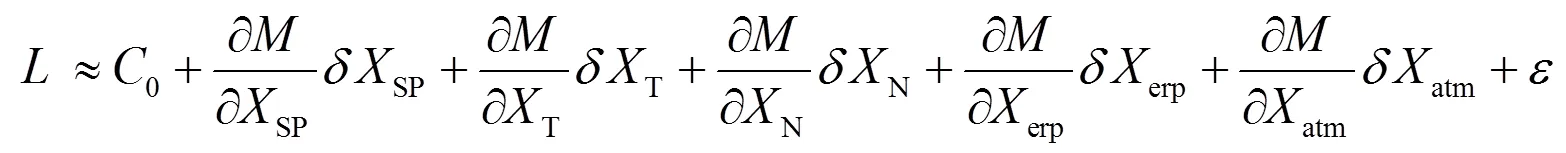
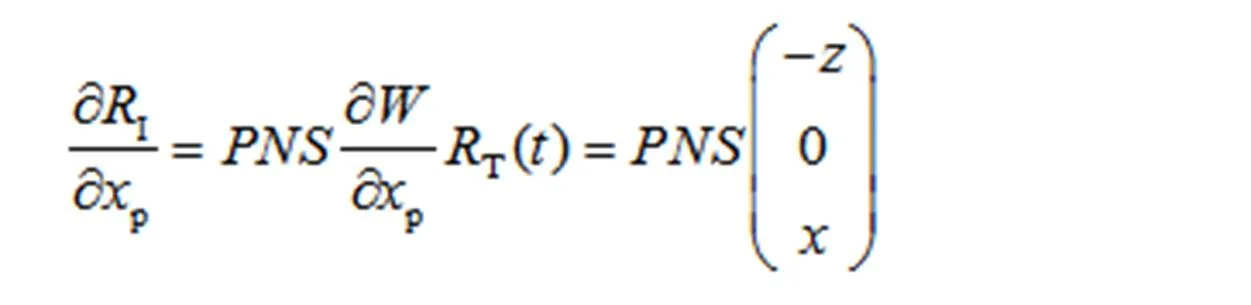
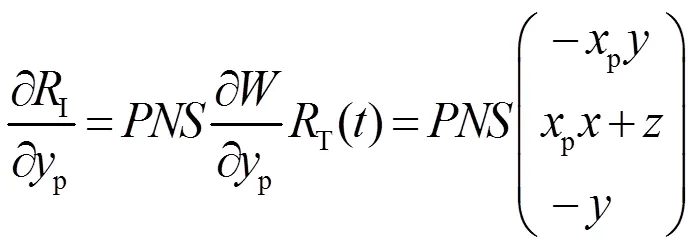
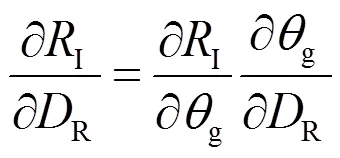
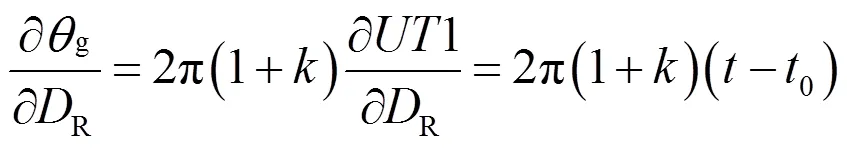
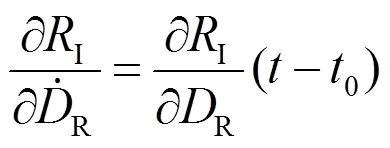
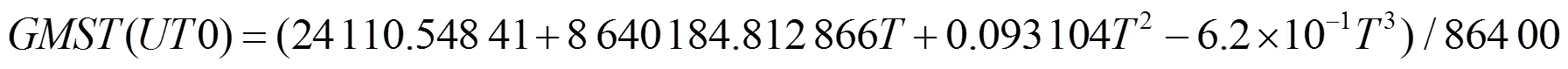
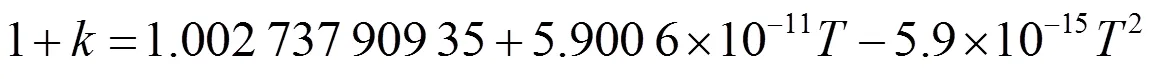
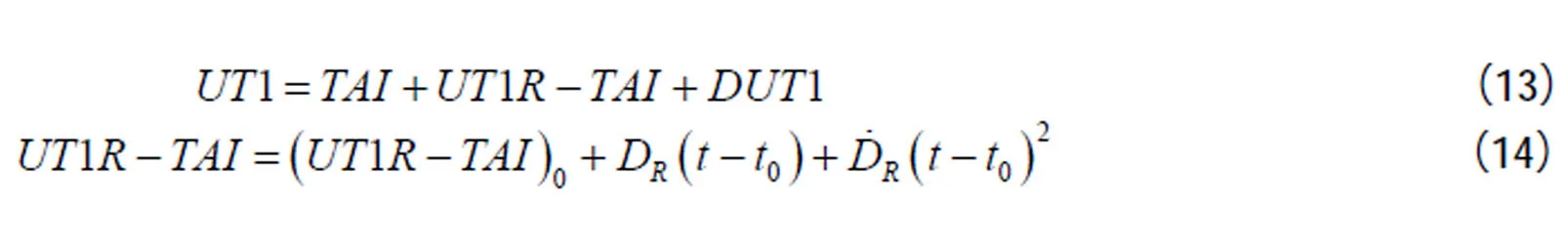
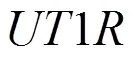
在本文的解算工作中，GPS載波相位為觀測量，維護ITRF2005框架的站坐標和衛星軌道參數來自IGS，解算量是地球自轉參數和大氣延遲參數[3]。

2 選站及數據準備

GAMIT軟件[2]處理GPS載波相位觀測量，采用雙差模式，處理時間隨著站數的增加呈幾何級數增加。由于現有計算機硬件條件的限制，從目前的302個IGS05參考框架站中優選了22個站，這22個站構成的網幾何分布良好、資料穩定：在ITRF2005框架中的坐標中誤差都在1 mm以下，速度場中誤差都在0.3 mm/y以下，分布圖如圖1（★表示所選站）所示。僅3個站的中誤差較大：ASPA站在方向的坐標中誤差為4 mm，速度場中誤差0.8 mm/y；BILI站在方向的坐標中誤差為3 mm，速度場中誤差0.5 mm/y；GLPS站在方向的坐標中誤差為2 mm，速度場中誤差0.4 mm/y[11]。在本文工作中選取22個站的情況下，每解算一次需要8 h左右。

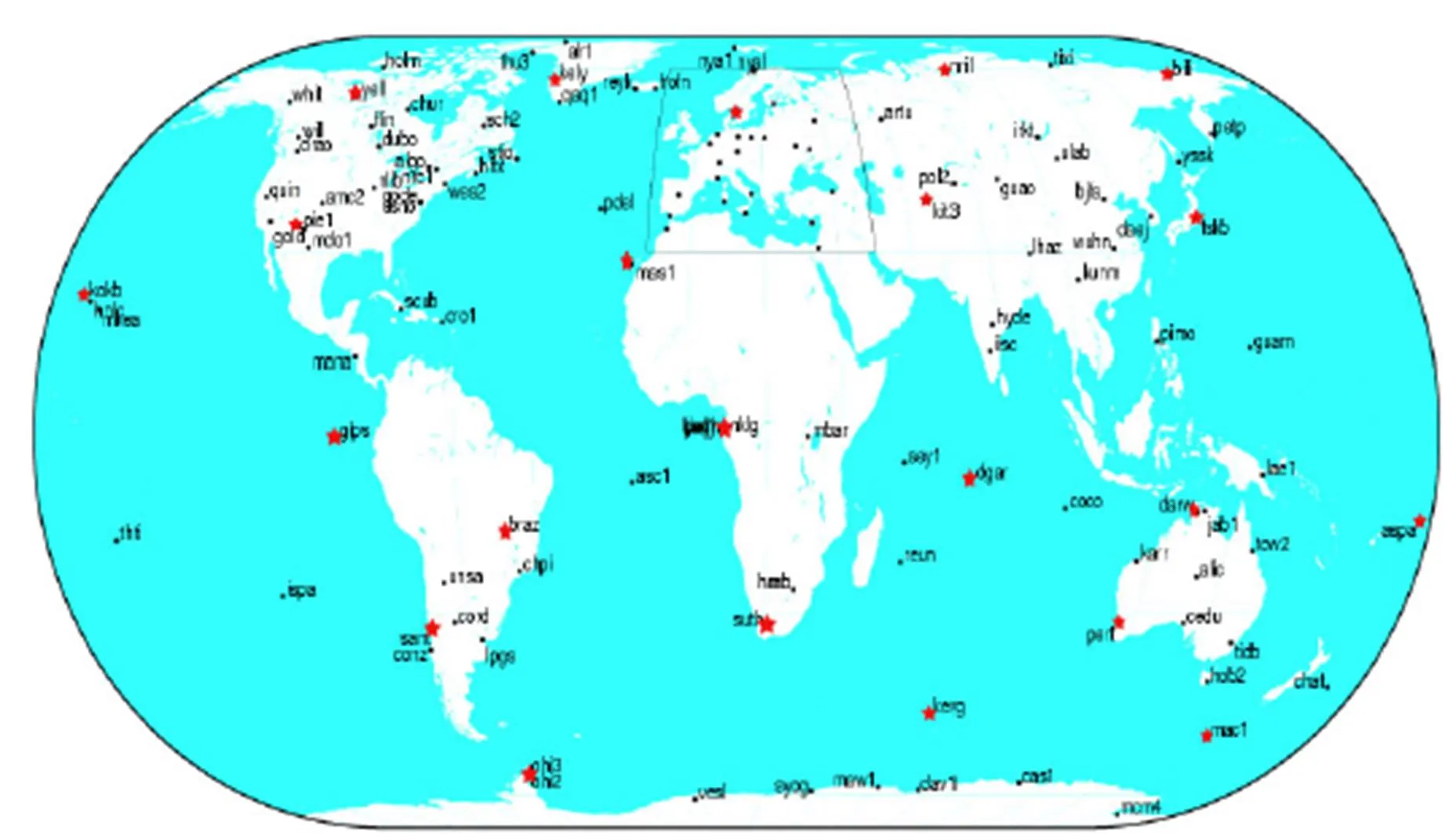
圖1 選擇的IGS站分布圖

從IGS站下載2007年9月11日至10月26日期間的觀測資料、導航文件和精密星歷，在ITRF2005框架下J2 000.0時刻的跟蹤站坐標與速率，用以計算跟蹤站對應時刻的初始坐標。站坐標由下式算得：

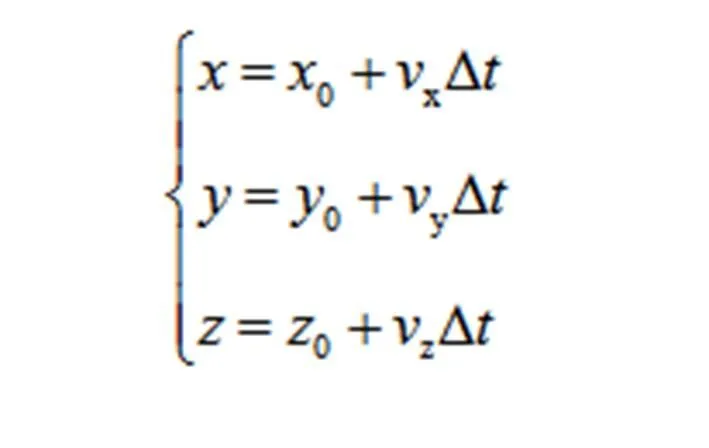
3 誤差源分析與精度評定

在解算中，我們估計了所有能估計的參數，包括站坐標、衛星軌道參數、光壓參數、地球自轉參數和對流層延遲等。

采用IGS所給精密星歷和光壓參數（BERNE模型），并給予站坐標、衛星軌道參數和光壓參數以強約束，這樣就基本保證我們在ITRF2005參考架中進行解算。

為了保證所用光壓模型的一致性，我們刪除了衛星處于地影中的觀測資料；用Saastamoinen模型[3-4]計算對流層延遲的初值，每30 min估計1個對流層延遲值。為了保證對流層延遲估計的精度，僅用10°仰角以上的觀測資料。

在GAMIT軟件[3]的MODEL模塊中，考慮了毫米級以上的系統差。所考慮的改正包括：站鐘和星鐘差的改正、相對論效應改正、衛星天線和測站接收機天線相位中心的改正、天線的電磁波右圓極化改正、對流層延遲改正、高階電離層延遲改正、固體潮改正、極潮改正和海潮改正等[3-4]。

解算結果的精度與可靠性通過兩個主要標準評判：1）是否有足夠的資料，該標準通過所得基線分量的精度來衡量；2）對資料的擬合模型是否與它的噪聲水平相稱，該標準通常采用歸一化均方根（normalized rms，簡寫為nrms）作為判據，其表達式為

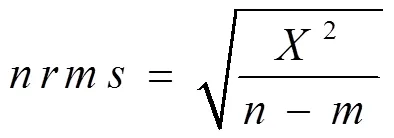
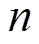
4 解算結果與分析

利用每24 h的數據估計數據段中點時刻的地球自轉參數。我們估計了每日UTC 12:00:00和UTC 00:00:00的地球自轉參數，經過剔除異常值及參數轉換后[12-15]，分別與IGS EOP（UTC 12:00:00）和IERS C04（UTC 00:00:00）同時刻的值進行了比較。為了檢驗解算結果，又將IGS EOP系列與IERS的C04系列分別進行比較。

1）本文結果與IGS EOP同時刻值之間的比較

IGS提供每日UTC 12:00:00時刻的地球自轉參數，時間分辨率為1 d，2007年9月10日至10月26日期間IGS EOP系列中的地球自轉參數值減去剔除異常值及參數轉換后的本文結果之差值如圖2～圖4所示。這些差值的標準差分別為：0.011 8 mas，0.013 6 mas和0.025 3 ms，差值均方根RMS分別為0.021 4 mas，0.066 2 mas和0.026 0 ms。

圖2 極移在x方向的分量之差值（xp（IGS）- xp（本文結果））

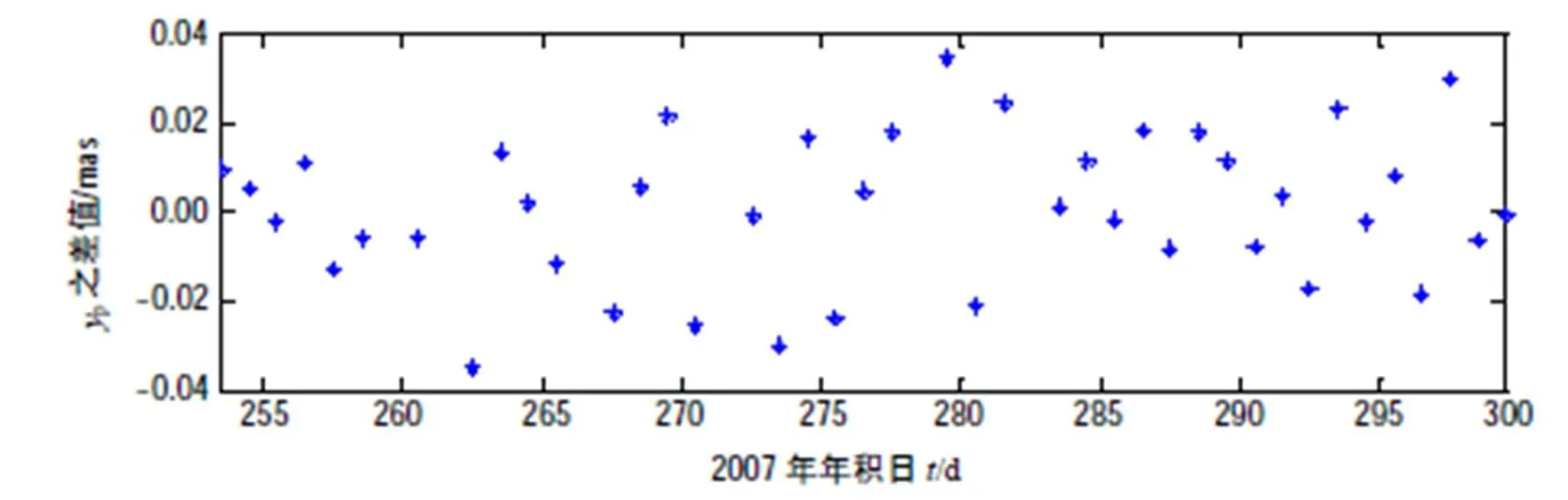
圖3 極移在y方向的分量之差值（yp（IGS）- yp（本文結果））

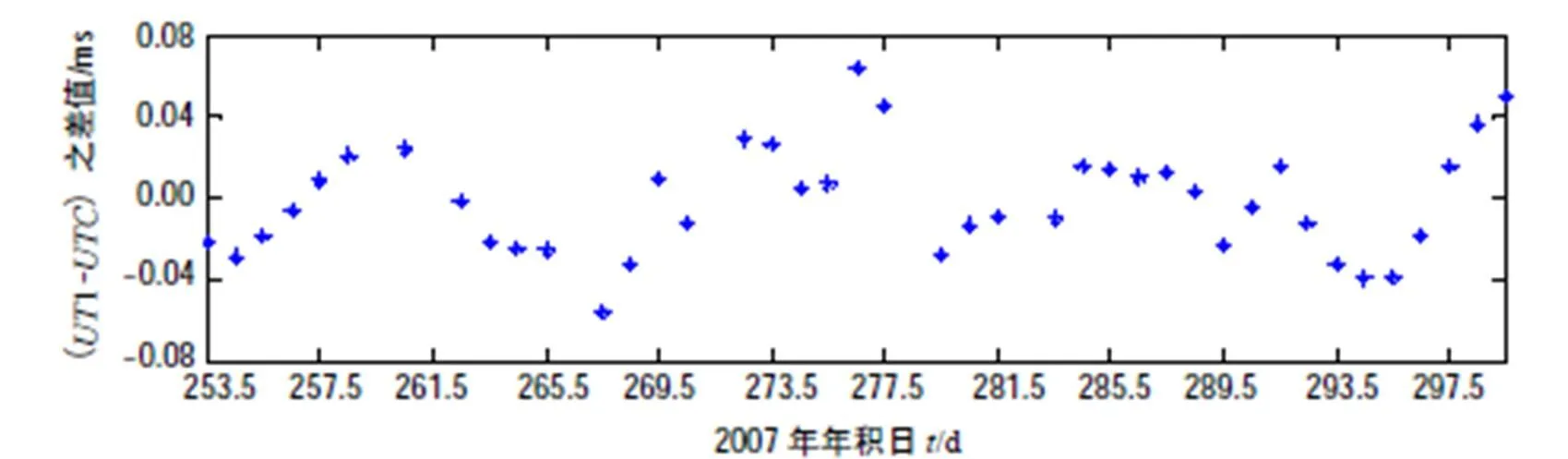
圖4 UT1-UTC之差值（（UT1-UTC）（IGS）-（UT1-UTC）（本文結果））

2）本文結果與IERS C04同時刻值之間的比較

IERS提供每日UTC 00:00:00時刻的地球自轉參數，時間分辨率為1 d，2007年9月10日至10月26日期間IERS C04系列中的地球自轉參數值減去經剔除異常值及參數轉換后的本文結果之差值如圖5～圖7所示。這些差值的標準差分別為：0.006 5 mas，0.010 9 mas和0.001 3 ms，差值均方根RMS分別為0.020 3 mas，0.035 4 mas和0.001 6 ms。

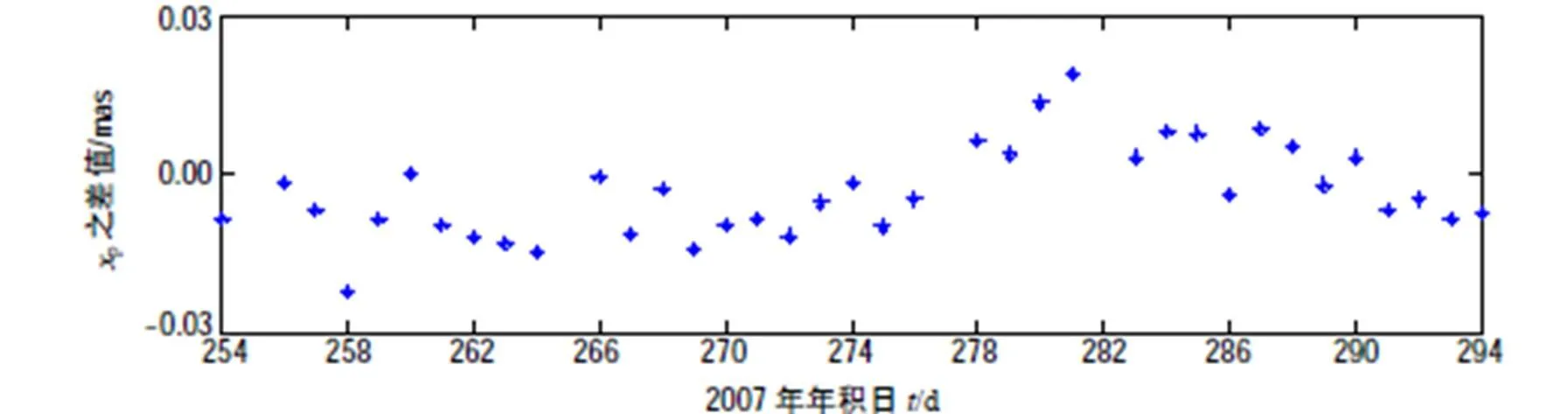
圖5 極移在x方向的分量之差值（xp（IERS）- xp（本文結果））

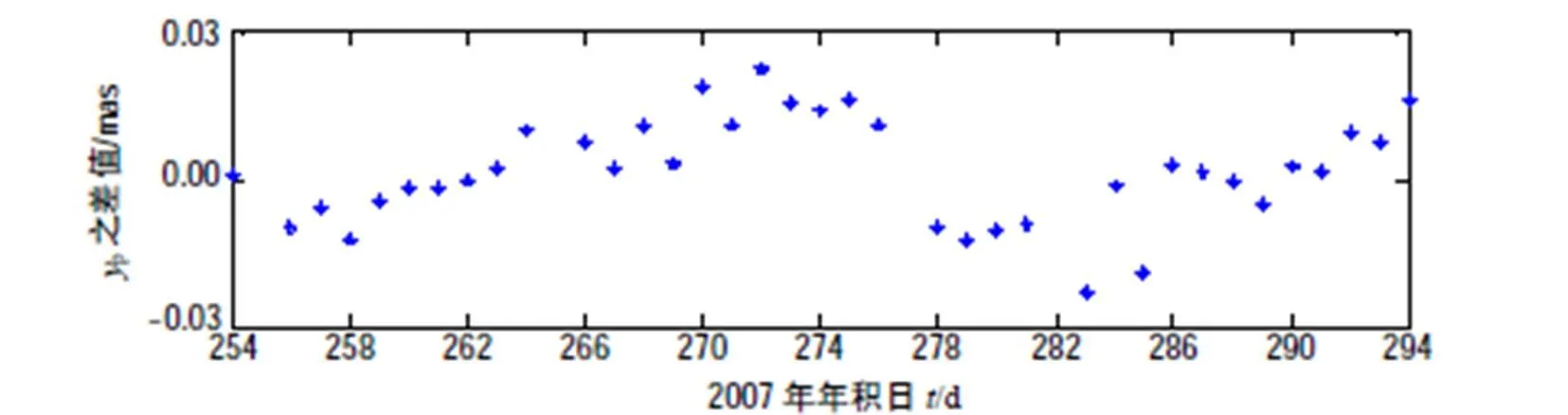
圖6 極移在方向的分量之差值（p（IERS）-p（本文結果））

圖7 （1-）之差值（（1-）（IERS）-（1-）（本文結果））

3）IGS EOP與IERS C04同時刻值之間的比較

在線將IGS 最終的EOP系列與IERS C04系列進行比較[16]，其中，IERS C04系列減去IGS EOP系列內插到UTC 00:00:00的系列的差值如圖8～圖10所示。

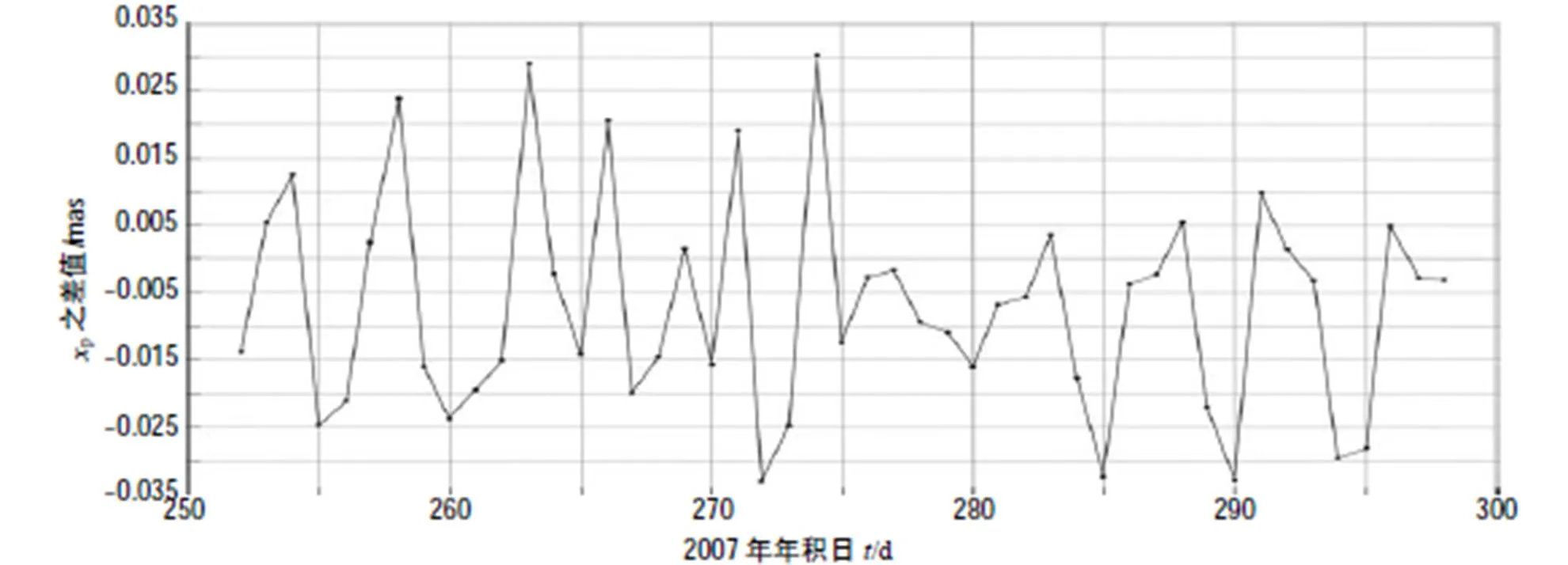
圖8 極移在x方向的分量之差值（xp（IERS）- xp（IGS））

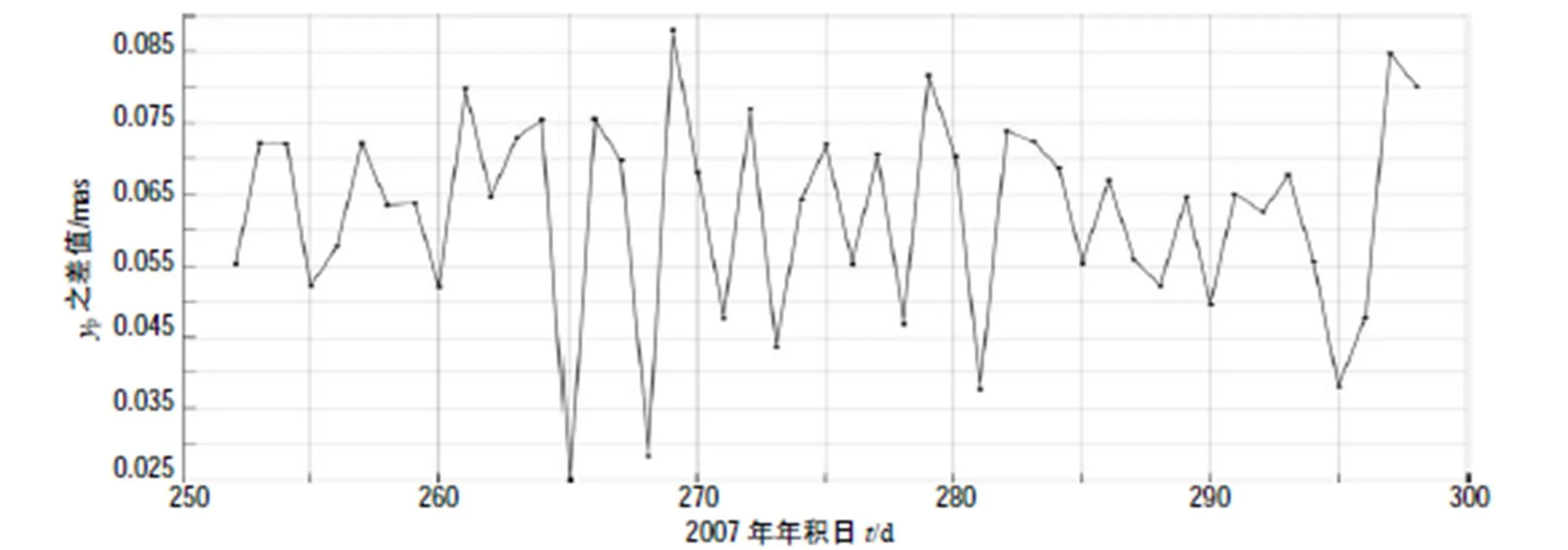
圖9 極移在y方向的分量之差值（yp（IERS）- yp（IGS））

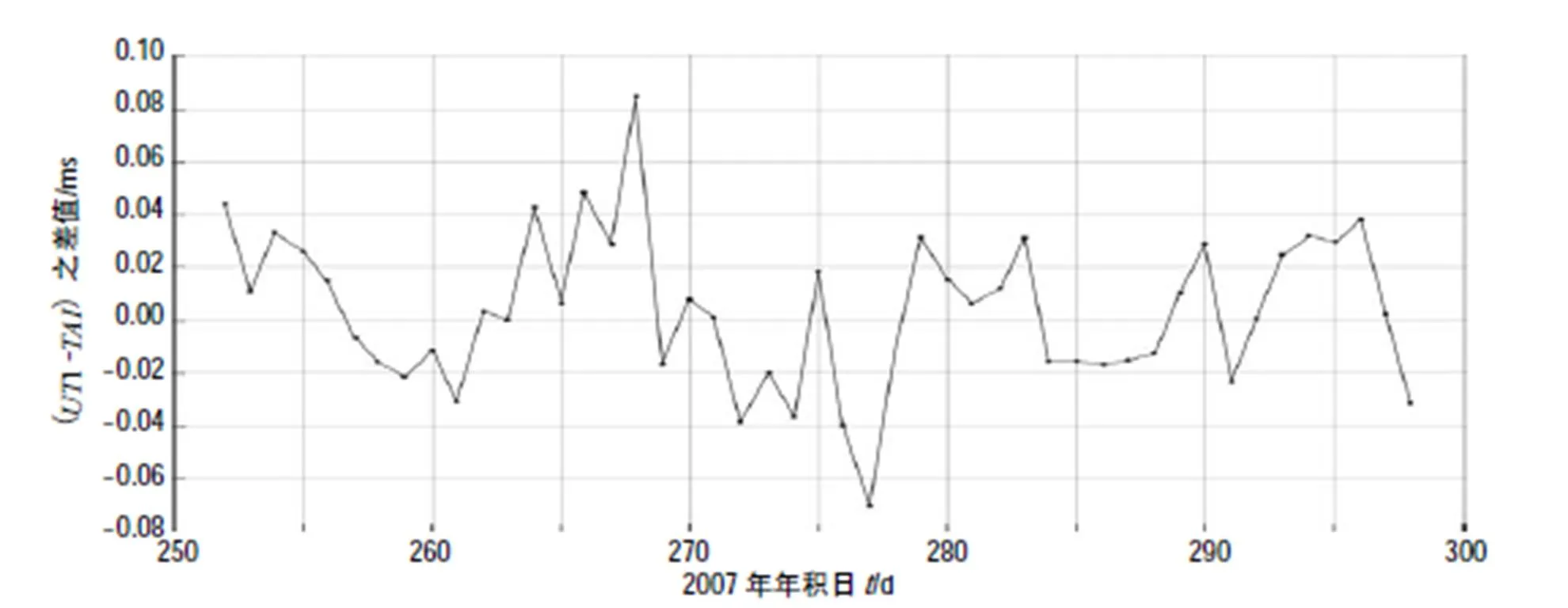
圖10 （UT1-TAI）值之差值（（UT1-TAI）（IERS）-（UT1-TAI）（IGS））

解算結果與IGS EOP 和IERS C04之間存在系統差。與IGS EOP在方向有0.01 mas的系統差，在方向有-0.06 mas的系統差；與IERS C04在方向有-0.015 mas的系統差，在方向有0.03 mas的系統差；1-之間沒有明顯系統差。

2007年9月10日至10月26日期間的計算結果除了個別天（5 d）異常外，大部分結算結果與IGS EOP、IERS C04同時刻值符合較好，剔除異常值及參數轉換后分別與IGS EOP、IERS C04的差值范圍和RMS如表1所示。本文解算結果的精度與IERS目前的精度基本相當。其中個別天的解算結果與IGS EOP、IERS C04同時刻的差值偏大，這與CONT02聯測后CODE的解算結果與IERS C04比較也出現了個別天差值偏大的情況相同[17]，需要選取更多IGS站予以解決。

表1 解算結果與IGS EOP和IERS C04的比較

5 結論

由于受到所用計算機的限制，我們目前的工作中只能挑選22個IGS 觀測站。但所選的22個觀測站遍布全球，且分布均勻，站本身的地質條件良好（所在板塊運動速度小且穩定）。用這些站的資料所計算得到的地球自轉參數的精度在 IERS C04所給相應值的精度范圍之內，我們解算的地球自轉參數結果是可信的。

[1] 李志剛, 楊旭海, 李偉超, 等. 轉發器式衛星測軌方法[J]. 時間頻率學報, 2006, 29(2): 81-89.

[2] 朱元蘭, 馮初剛, 張飛鵬. 用中國衛星激光測距資料解算地球定向參數[J]. 天文學報, 2006, 47(4): 441-449.

[3] Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology. Documentation for the GAMIT GPS Analysis Software[Z]. Massachusetts: Massachusetts Institute of Technology, 2000.

[4] Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology. GAMIT Reference Manual[Z]. Massachusetts: Massachusetts Institute of Technology, 2006.

[5] GAMBIS D, BIZOUARD C, SA?L M. Evolution of Earth Orientation Monitoring At IERS[C] // Proceedings of the "Journées 2005 Systèmes de Référence Spatio-Temporels". [S.l]: [s.n.], 2006: 59-61.

[6] XU Guo-chang. GPS Theory, Algorithms and Applications[M]. 2nd ed. Berlin: Springer, 2007.

[7] 李濟生. 人造衛星精密軌道確定[M]. 北京: 解放軍出版社, 1995: 26-33.

[8] 劉根友. 高精度GPS定位及地殼形變分析若干問題的研究[D]. 武漢: 中國科學院測量與地球物理研究所, 2004: 31-36.

[9] 陳俊勇. 走向新世紀的GPS[J]. 衛星應用, 2000, 8(2): 26-31.

[10] 周忠謨. GPS衛星測量原理與應用[M]. 北京: 測繪出版社, 1997.

[11] ITRF. ITRF 2005 Station Positions at Epoch 2000.0 and Velocities GPS Stations[DB/OL]. (2006-10-27)[2009-09-01]. http://itrf.ensg.ign.fr/ITRF_solutions/2005/doc/ITRF2005_GPS.SSC.txt.

[12] ZHU Sheng-yuan, MUELLER II. Effects of Adopting New Precession, Nutation and Equinox Corrections on the Terrestrial Reference frame[J]. Journal of Geodesy, 1983, 57(1): 29-42.

[13] 蔣虎, 黃珹, 馮初剛. 極移序列系統差的探討[J]. 中國科學院上海天文臺年刊, 2000, 21: 19-23.

[14] 趙銘. 天體測量學導論[M]. 北京: 中國科學技術出版社, 2006: 107-109.

[15] DICK W R, RICHTER B. IERS Annual Report 2000[R]. [S.l]: [s.n.], 2001: 97-98.

[16] IERS. Eop Series (Mostly Operational) Comparison[DB/OL]. (2009-03-24)[2009-09-01].http://hpiers.obspm.fr/eop-pc/products/operational/operational.html.

[17] NASTULA J, KOLACZEK B, WEBER R, et al. High Resolution Earth Rotation Parameters Determined During the CONT02 Campaign[C] // International VLBI Service for Geodesy and Astrometry 2004 General Meeting Proceedings. Ottawa: [s.n.], 2004: 9-11.

Estimation of Earth Rotation Parameters Based on GPS Observations

HE Zhan-ke1,2, YANG Xu-hai1, LI Zhi-gang1, CHENG Zong-yi3

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 2. Graduate University of the Chinese Academy of Sciences, Beijing 100039, China;3. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China)

Earth rotation parameters; GPS; IGS(International GNSS Service); IERS(International Earth Rotation Service)

2009-08-03

國家高技術研究發展計劃（863計劃）資助項目（2006AA12Z322）；國家重點基礎研究發展計劃（973計劃）資助項目（2007CB815503）；中國科學院知識創新工程重要方向資助項目（KJUX2-YW-T12）; 中國科學院國防科技創新資助項目（CXJJ-09-M34）。

何戰科，男，碩士，主要從事GPS高精度數據處理和衛星導航定位技術應用方面的研究。

P228.4

A

1674-0637(2010)01-0069-08