遺傳算法在水力管網優化中的應用

張 進,王衛敏,荊振鋒,趙有民

(1.陜西城鎮規劃建筑設計研究院,西安710068;2.西安建筑設計研究院,西安710054;3.延安熱電廠,延安716000)

0 引言

水力管網優化的實質是,在水力約束條件下,確定使目標函數即綜合費用 (包括初投資和設計年限內的運行費用)為最小的變量 (管徑)。這類問題在數學分析中稱為極值問題,在統計數學中稱為最優化問題。傳統的求解非線性優化問題的方法對管網優化模型進行求解時必須先假設管徑是連續變量,同時在求解過程中必須對目標函數進行求導,因此,在實際應用中受到了限制。本文嘗試將遺傳算法應用到水力管網的優化中,相對于傳統的優化方法,遺傳算法直接針對實際規格的管徑,計算簡便易行,只包括復制、交叉、變異這幾個簡單的過程。

1 遺傳算法簡介

遺傳算法其實質是一種由計算機完成主要計算過程的迭代方法。遺傳算法起源于20世紀60年代對自然和人工自適應系統的研究[1],最早由美國密執安大學的Holland教授提出。遺傳算法借鑒了達爾文的自然進化理論與孟德爾的遺傳變異理論,通過選擇一定數量的個體進行雜交以及基因突變,把優秀的基因傳給后代,丟棄不良基因,經過數代遺傳,最終得到最優秀的一個或幾個后代 (問題的最優解)。

遺傳算法已用于求解帶有應用前景的一些問題,例如遺傳程序設計、函數優化、排序問題、人工神經網絡、分類系統、計算機圖像處理和機器人運動規劃等。遺傳算法經過很多人的改良也產生了很多變種,本文所涉及的遺傳算法僅指 “簡單遺傳算法”簡稱SGA。與傳統優化算法相比,SGA具有以下特點[2]:(1)搜索過程不直接作用在變量上,而是作用在將變量編碼后的字符串上;(2)搜索過程從一組解迭代到另一組解,降低了陷入局部最優解的可能性;(3)搜索過程是隨機的而非確定性的;(4)對搜索空間沒有任何特殊要求,不需要導數等其它輔助信息。

2 遺傳算法解決優化問題的主要步驟

從技術經濟觀點來看,任何輸配系統的方案,均可用工程造價和運行費用來評價。

2.1 管徑編碼

編碼是遺傳算法的第一步,采用二進制編碼方案。為便于討論,水力管網的管材選用無縫鋼管(GB8163-87)系列,實際應用時選用其他管材無非價格不同而已。取8種規格的鋼管進行編碼,如表1所示。

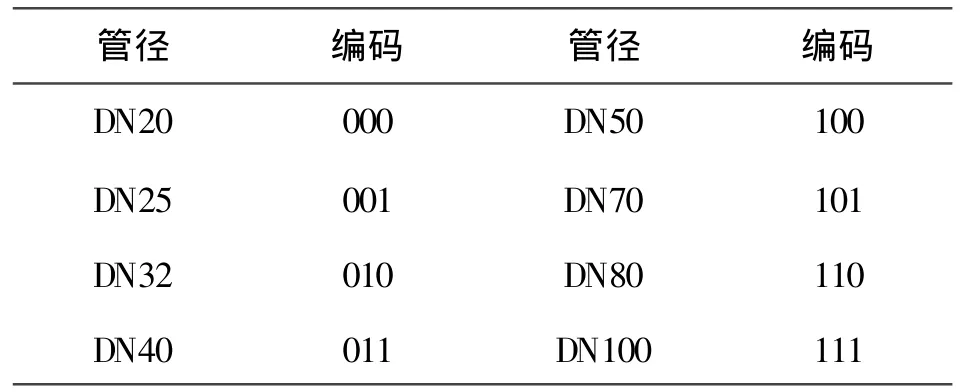
表1 管徑編碼表

2n種規格的鋼管編碼便有n位。

管徑編碼完成后,管網的設計方案即可用按管段編號順序排列的一串0,1字符表示。例如,由8根管段組成的管網的公稱管徑按管段號排列依次為:20,25,25,32,40,32,70,80,那么對應的二進制表示的字符串則為:000|001|001|010|011|010|101|110。這個二進制字符串在遺傳算法中稱為遺傳算子,也叫染色體。

以8根管段組成的管網為例,算法第一步就是隨機產生一定數量的染色體,每個染色體為24位字節的二進制數即可。染色體總數叫種群規模,它對算法的效率有明顯的影響,規模太小不利于進化,而規模太大將導致程序運行時間長。建議對管網優化問題,此規模取30至100。

2.2 適應度函數

為了體現染色體的適應能力,引入了對問題中的每一個染色體都能進行度量的函數,叫適應度函數。通過適應度函數來決定染色體的優、劣程度,它體現了自然進化中的優利劣汰原則。

管道的初投資取決于材料費和安裝費。管道的安裝費在管道敷設深度、土壤和路面性質、管子連接方法、施工機械化程度確定后則由管徑決定,一般來說管徑變化對安裝費影響不大。

管網的運行費用主要由電費和維修費組成,維修費受當地管理水平限制一般與初投資成正比,電費與流量和壓降的乘積成正比,而壓降在管徑確定后則由流量決定。

工程實際中,已知管網總流量,給定各管段管徑后,根據連續性方程,并聯管段阻力相同和水力計算的經驗公式可由電腦計算出各管段流量。有了管徑和流量就可以計算出初投資和設計年限內的運行費用 (也由電腦自動完成),得出費用評價函數W=∑[f(di)+g(di,qi)]。式中f(di)為初投資費用,是管徑的函數,單位為元。g(di,qi)為運行費用,是管徑及流量的函數,單位為元。di為各段管徑,單位為mm。qi為各段流量,單位為噸每小時。

可見每個染色體唯一對應一個綜合費用,從而可以用綜合費用評價染色體的優劣。管網優化計算中應該費用越低則適應度越大,才能達到管網優化的目的。按照這個要求,通常可以將適應度函數取為與費用評價函數W成反比,即:f=1/W,也可取與W平方成反比。

2.3 遺傳操作

簡單遺傳算法的遺傳操作主要有三種:選擇、交叉、變異。

2.3.1 選擇操作 選擇的目的是把優化的染色體直接復制到下一代或通過配對交叉產生新的染色體再遺傳到下一代。這里采取配對交叉遺傳的方式。選擇機制為適應度比例選擇機制,也叫賭輪或蒙特卡羅選擇。在該機制中,每個染色體的選擇概率為其適應度值除以所有染色體適應度值之和,適應度值大的染色體被選擇的幾率較高。同時,采用最佳個體保存方法,把群體中適應度值最大的染色體不進行配對交叉而直接復制到下一代中,這樣,可以保證產生的新一代群體的最大適應度值不會小于上一代。Radolph在文獻 [3]中證明了遺傳算法不一定收斂,只有每代保存了最優個體時才收斂。在實際應用中,使用了上述結論來保證收斂性。采用優秀個體保護法就是將每代中的最優個體,直接進入子代。

對保存最優個體時遺傳算法是收斂的結論的證明是通過對遺傳算法構造馬爾柯夫 (markov)鏈,因為遺傳算法的進行過程是一個馬爾柯夫過程。

注:馬爾柯夫鏈。狀態是指某一事件在某個時刻 (或時期)出現的某種結果。事件的發展,從一種狀態轉變為另一種狀態,稱為狀態轉移。在事件的發展過程中,若每次狀態的轉移都僅與前一時刻的狀態有關,而與過去的狀態無關,或者說狀態轉移過程是無后效性的,則這樣的狀態轉移過程就稱為馬爾柯夫過程。馬爾柯夫鏈是參數t只取離散值的馬爾柯夫過程。

2.3.2 交叉操作 交叉是模仿自然界有性繁殖的基因重組過程,其作用是將原有的優良基因遺傳給下一代個體,并生成包含更復雜基因結構的新個體。交叉操作是遺傳算法區別于其他所有優化算法的根本所在,如果從一個遺傳算法中去掉交叉操作,則其結果將不再是一個遺傳算法[4]。

交叉操作是將被選擇出的兩個個體P1和P2作為父母個體,將兩者的部分碼值進行交換。對于24位的染色體:由電腦隨機產生一個在1到24之間的隨機數c,假如現在產生的是3,將P1和P2的低3位交換:P1的高21位與P2的低3位組成一個新染色體,這就是P1和P2的一個后代Q1個體;P2的高21位與P1的低3位組成另一個新染色體,這就是P1和P2的一個后代Q2個體。

2.3.3 變異操作 變異是模擬自然界生物體進化中染色體上某位基因發生的突變現象。變異可以使搜索避免陷入局最優,可以在當前解附近找到更好的解,同時還可以保持群體的多樣性,確保群體能夠繼續進化[4]。

對于24位的染色體:由電腦隨機產生一個在1到24之間的隨機數d,假如現在產生的是3,將原染色體的第3位0和1互換產生一個新染色體。

2.3.4 操作的控制參數 不是每個被選擇了的染色體都進行交叉操作和發生變異,而是以一定的概率進行,一般在程序設計中交叉發生的概率要比變異發生的概率選取的大若干個數量級,交叉概率取0.6至0.95之間的值;變異概率取0.001至0.01之間的值。個人建議設定一大一小兩個變異概率,當整個種群平均適應度增長較快時,使用小變異概率;反之使用較大變異概率。

2.4 算法的終止條件

遺傳算法的一般循環終止條件為設定最大進化代數,個人建議取50～80次。也可以把解的質量作為判據,如連續幾次得到的最優個體的適應度沒有變化或變化很小時,則認為算法收斂,循環終止。再次,種群中最優個體的適應度和群體的平均適應度的差除以群體平均適應度,所得的結果小于某一給定允許值,也可以作為循環終止的條件。

2.5 染色體解碼

終止后輸出種群中適應度值最優的染色體,對其進行解碼得到管網各管段的管徑。解碼就是管道編碼的逆運算。

2.6 遺傳算法解題步驟的總結

根據遺傳算法思想可以畫出如圖1所示的簡單遺傳算法框圖。

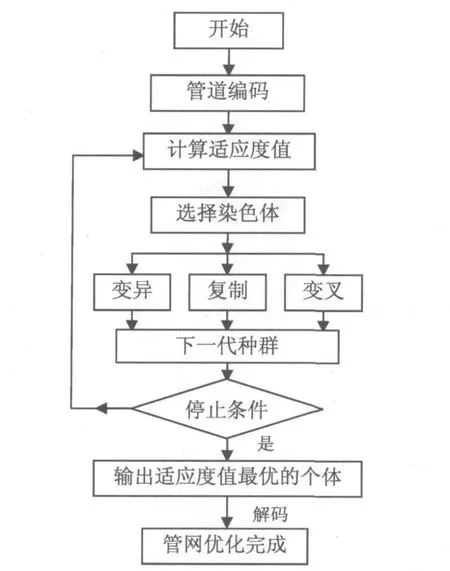
圖1 簡單遺傳算法示意圖

遺傳算法的主要步驟如下:

(1)隨機產生一個由確定長度的染色體組成的初始群體。

(2)對該染色體群體迭代地執行下面的步驟①和步驟②直到滿足停止準則為止:

①計算群體中每個染色體的適應值;

②應用復制、交叉和變異等遺傳操作產生下一代群體。

(3)達到終止條件后,把后代中出現的最好的染色體輸出為遺傳算法的執行結果,這個結果可以解碼為問題的一個解。

2.7 算例描述

某管網連接圖見圖2。共有7個節點,6條管道連接路線。管網中各個節點需水量和長度見圖示,管道單價經驗公式為:

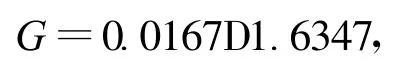
管徑D的單位為mm,適應度函數取為與費用評價函數W成反比,即:

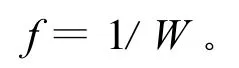
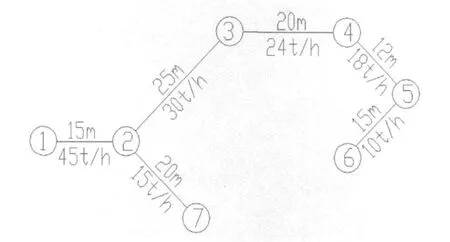
圖2 某管網連接圖

對此管網應用遺傳算法進行優化布置,設置群體規模為30,設定最大進化代數為50代,進行計算。

以下列出最后三步的最優解 (見表2)。

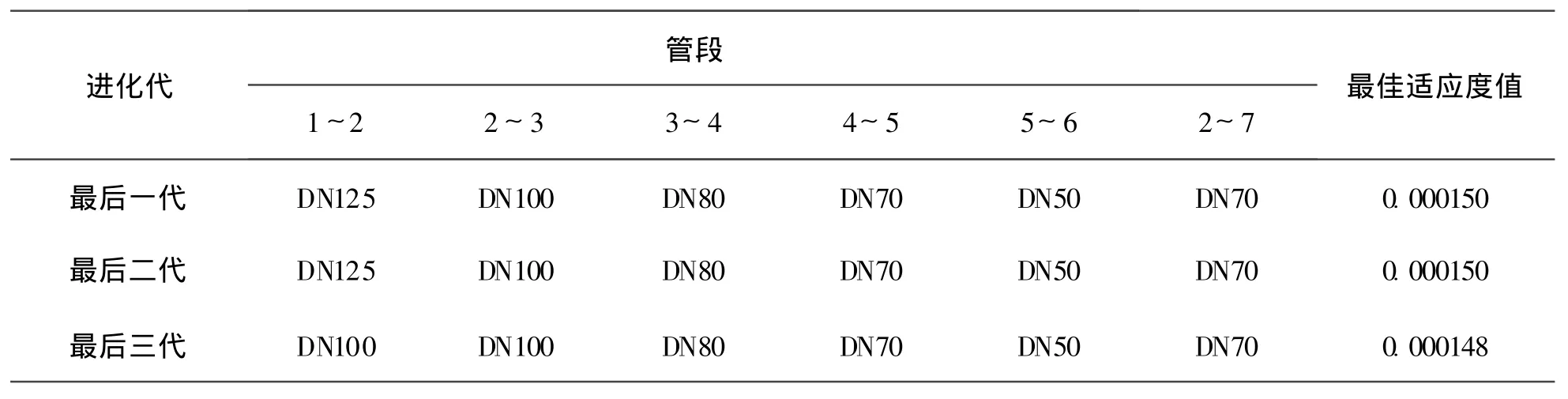
表2 最后三步的最優解

3 結語

遺傳算法在計算結果以及收斂速度方面具有優勢,但是算法的參數選取直接影響到算法的效果,需要進一步研究。

此外,管網系統是個復雜的系統工程,本文中未對當地水文地質條件、政策、物價的波動等因素做深入考察,需要進一步研究加以完善。

[1] HOLLAND J H.Adaptation in nature and artificial systems[M].Michigan:The University of Michigan Press,1975

[2] 周明,孫樹棟.遺傳算法原理及應用 [M].北京:國防工業出版社,1999

[3] Qi X F;Palmieri theoretical analysisof evolutionary algorithms with an infinite population size in continuous space(Part,)[M].IEEE Transactions on Neural Network;1994

[4] 張鈴,張鈸.遺傳算法機理的研究[J].軟件學報,2000,(7):945-952