中心差分法在燃氣管道動態模擬中的應用*

高蘭周 侯根富 王 東

0 引言

天然氣長輸管線不穩定流動的基本方程組可以利用分離變量的方法求出解析解,但是要通過簡化和復雜的數學變換,求解比較復雜。而且求解的結果與實際運行中的管道有一些差別。如果利用數值求解,就不存在上述問題。

在對本問題的數值解法中,有特征線法、隱式差分法和顯示法等。對于特征線法,可將管道上的偏微分方程化為特征差分方程,不用求解龐大的非線性方程組,占用較少的計算機內存,易于求解,計算速度快,但為了滿足求解的穩定性,時間層次往往取得很小。然而,對于天然氣管網系統而言,由于氣體的可壓縮性,其出現不穩定程度要比液體管道出現的不穩定程度小得多,因而時間層次取得過小沒多大的意義,還會浪費計算時間。對于隱式差分法,由于要將待求時間層次上所有的未知量聯立起來進行求解,需要求解的非線性方程組非常龐大,求解需要較長的時間。但是這種方法能夠保證求解的穩定性,時間步長可取得較大[1]。

1 數學模型的建立

天然氣長輸管線的管徑在很長的距離上是不變的,因此垂直于流線的氣體特性變化率同沿著流線的變化率相比可忽略不計,而且管道的曲率半徑比管道的直徑大得多,因此流動可以看作是一元流動,在管道任意一截面上所有流體參數都可以看作是均一的,為該斷面的平均值。本文采用以下數學模型[1,2]。

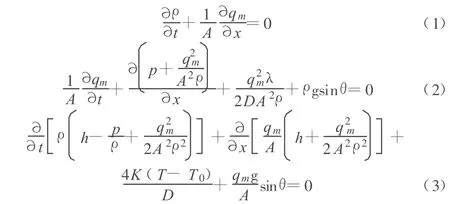
其中,ρ為燃氣密度,kg/m3;t為時間,s;A為管段的流通橫截面面積,m2;qm為質量流量,kg/s;x為管段軸向長度,m;p為氣體壓力,Pa;λ為摩阻系數;D為管道內徑,m;g為重力加速度,m/s2;θ為燃氣管道對水平面的傾斜角,rad;h為比焓,J/kg;K為傳熱系數,W/(m2?K);T為燃氣溫度,K;T0為土壤溫度,K。

2 差分格式的建立和方程組封閉的分析

非穩態氣體狀態方程(1)～方程(3)及實際氣體狀態方程p=p(ρ,T)和比焓方程 h=h(ρ,T)可以用更一般的形式來表示,即為=0。此方程為一階雙曲型方程。對于此形式的偏微分方程,考慮選用有時步和距步二階精度的Wendoff差分格式[3,4]。

為了求解所形成的差分方程,還需確定輸氣的邊界條件和初始條件。邊界是對系統而言的,現定義一段管子為研究對象,管子兩端的連接情況及相應的運行控制情況為邊界條件。對一大型輸氣管網,邊界條件可能是多種多樣的,主要有:氣源、一個管子的終點且有分氣量、管子與管子的相交節點且有分氣量,如忽略節點的局部阻力和速度的差別則各支管節點壓力和溫度相等、節點控制最小壓力[5]。

結合一典型的輸氣工藝流程進行封閉性分析[6]。

該輸氣干線中由4支管段,5個節點組成,其中節點1是氣源,節點3,4,5是分氣點,節點2是普通節點,將每一段管線進行剖分,得截面為n1,n2,n3,n4,因為每個截面有3個未知變量p,qm,T,所以共有未知變量3?(n1+n2+n3+n4)。

可建立的差分方程數為:3?(n1-1)+3?(n2-1)+3?(n3-1)+3?(n4-1)。

按上面的邊界條件確定方法,上游邊界條件有兩個,即氣源的壓力與溫度,下游分氣點的邊界條件有四個,即例中的 qm(t)或p≥pmin,不能兩者兼有,對節點2和節點3可建立節點壓力、溫度或密度和流量3個平衡方程,共計6個方程。

因此共有邊界條件:2+4+6=12;

因為:3(n1-1)+3(n2-1)+3(n3-1)+3(n4-1)+12-3×(n1+n2+n3+n4)=0。

方程的個數與未知數的個數相等,因此方程是封閉的。

長輸管線不穩定流動數學模型的中心有限差分法計算格式及相應的初始條件,所形成的是一個非線性、非齊次的方程組。對一個剖面就有5個方程,那么對一個大型的輸氣管網將有多個方程,因此在選擇計算方程組的方法上,應該能夠快速逼近真值,考慮到該方程組易求導和迭代初值離真值的偏差較小,故考慮選用Newton-Raphson迭代法求解[3]。

3 計算實例分析

某市高壓管網半環(門站—調壓站 B—調壓站 C)管道長40 km,管道內徑為 700 mm,土壤溫度為278.15 K,氣體常數為8.314 5 J/(mol?K),已知各個管段步長節點的初始時刻質量流量、密度和溫度以及調壓站B和調壓站C 24 h的流量數據,氣源的密度和溫度恒定。

模擬時間為1 d,模擬程序用Visual C++語言編制,時間步長取3 600 s,管段步長計算網格為40個,即空間步長為1 km。選取部分時刻,其計算結果如下:

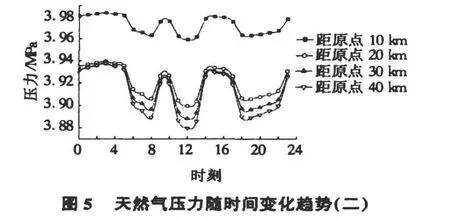
計算結果分析:圖1～圖3分別為天然氣的密度、溫度和壓力在同一時刻隨距離的分布。從圖1～圖3中可以看出天然氣的密度、溫度和壓力并不是線性分布的。它們在10 km處產生明顯而劇烈的變化,這是因為在10 km處存在分氣點,從而氣體壓力變化劇烈。同時氣體在此處有明顯的節流效應產生,因而溫度變化明顯。圖4,圖5分別反映了天然氣在同一點處的壓力隨時間變化的情況。由于用戶用氣量周期性變化,使得管網各處的壓力也是周期性變化的,該變化趨勢與用氣量的變化趨勢相反。由于在12:00及19:00,用戶用氣量最大,在此時刻,管道中的壓力卻最小;相反在用氣量的低峰時,管道內的壓力相對最大。另外,在分氣點前,其壓力變化的幅度小,而在分氣點后,氣體壓力變化的幅度大。圖6反映的是分氣點處的流量變化。從圖6中可以看出,在8:00,12:00及19:00等用戶用氣量較大,在3:00,15:00等用戶的用氣量較小,與實際用氣規律相符。

4 結語

采用了隱式差分法,對不穩定流動模型進行求數值解。通過研究可以得出如下結論:

1)數值解法對長輸管線不穩定流動進行研究。不用對模型方程組進行簡化和復雜的數學變換,因而求解出來的結果與實際運行中的數據更為接近;

2)求解時要將待求的時間層次上所有的未知量聯立起來同時進行求解,求解的非線性方程組非常龐大,方程組過大時求解需要較長的時間。為了保證數值解的絕對穩定性,因而時間、空間步長不能夠取的過小;

3)數值解考慮了氣體與外界環境的熱交換,能夠計算出天然氣沿線的溫度分布;

4)由于供氣與用氣的波動,導致管網中氣體的壓力、流量與溫度也是隨時間波動的。如果管網存在有分氣點時,在分氣點處氣體的壓力、溫度、密度的變化最為劇烈。

[1] 李長俊,曾自強,江茂澤.天然氣在管道系統中不穩定流動的分析[J].天然氣工業,1994,14(6):54-59.

[2] 隋元春.不穩定工況下燃氣管網的模擬計算[J].煤氣與熱力,1992(1):36-41.

[3] 翟瑞彩,謝偉松.數值分析[M].天津:天津大學出版社,2000.

[4] 李長俊.天然氣管道輸送[M].北京:石油工業出版社,2006.

[5] 周 游.天然氣長輸管線末段與城市高壓外環不穩定流動及末段儲氣的研究[D].濟南:山東建筑大學碩士學位論文,2004.

[6] 唐建峰,段長貴,呂文哲,等.特征線法在燃氣管道動態模擬中的應用[J].油氣儲運,2001,20(8):12-17.