常用分布分位數的關系及應用

孫祝嶺

（上海交通大學數學系，上海 200240）

0 引言

我們知道t分布、2χ分布、F分布和正態分布是統計分析中的幾種最常用分布，這些分布的分位數是統計分析的重要工具。然而，這些分布的分位數通常是要通過查表來獲得。

最近，有文獻[1]和[2]給出了有著重要應用價值的一些結果。其一，給出了正態分布變異系數的精確區間估計方法，它有多方面的應用，如可應用于結構可靠性的設計與估計，抽樣檢驗方案的確定，質量穩定性的評定等；其二，給出了分布自由時環境因子的置信估計方法。

環境因子在可靠性工程上有著重要應用。在可靠性評定、驗收中，經常要遇到不同環境下試驗數據的折算與綜合問題，如涉及航空航天產品的可靠性數據常常因為少得可憐而難以做出有效的可靠性分析，若能把其他環境下的可靠性數據折算為所考察的環境下的數據與已有少量數據加以綜合，則無疑會有助于提高可靠性分析的效果。這類問題的解決就是取決于環境因子的確定。另外，在可靠性預測、分配等工作中也離不開環境因子。

上述兩個結果中分別含有自由度是1的2χ分布、F分布的分位數。一般書中的有關分位數表對于每個自由度僅給出了為數不多的分位數值，在這些值外就查不到了。為便于應用，本文探討了分布t(1)、χ2(1)、F(1,1)和N(0,1)分位數的關系及計算方法；給出了分布N(0,1)分位數的一個新的簡單有效的計算公式，為統計分析提供了一個新工具。

1 分布 t(1)、χ2(1)、F(1,1)和 N(0,1)分位數的關系及計算

1.1 先推導分布t (1)和F(1,1)分位數之間的關系

設X～t(1)，則Y=X2～F(1,1)。

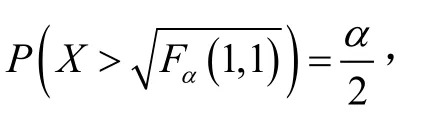
下面推導分位數Fα( 1 , 1)的表達式。

自由度為(1,1)的F分布F(1,1)的密度函數為

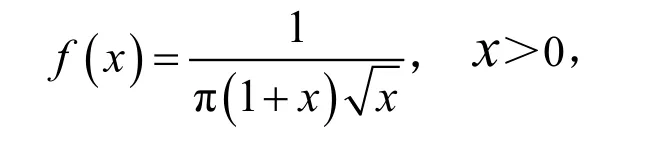
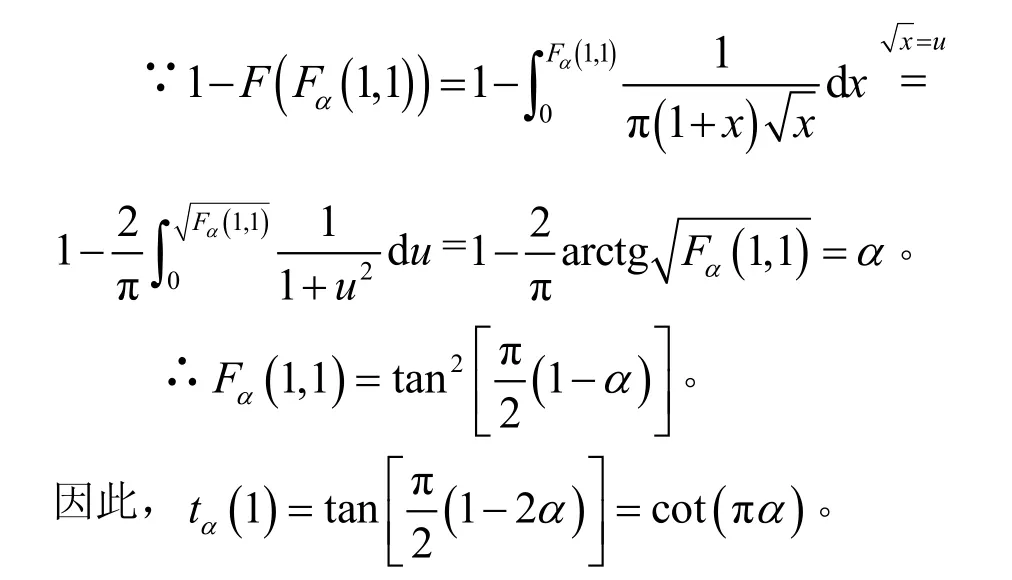
1.2 其次推導分布χ2(1)和N(0,1)分位數之間的關系

設ξ～N(0,1)，則η=ξ2～χ2(1)，

注：類似于1.1節和1.2節中的結論，在文獻[3]和[4]中有所涉及；但討論的目標、方法、結果形式卻不完全相同。

1.3 再給出分布t(1)和N(0,1)分位數之間的關系

應用常用的標準正態分布函數值表與t分布分位數表自由度為1的數據，應用Excel軟件，建立標準正態分布下側分位數z1-α關于自由度為1的t分布t(1)上側分位數tα(1)的回歸方程，見下面定理1。此回歸方程的判定系數為：R2=0.999 97；整體性檢驗的F統計量的值為：149 862.9；各回歸參數局部性的檢驗p值依次為：0.004 015，0.000 651，5.61×10-6。從這些數據可知方程高度有效。

定理 1: 分布t(1) 上側分位數tα(1)與分布N(0,1)下側分位數z1-α滿足下列等式：

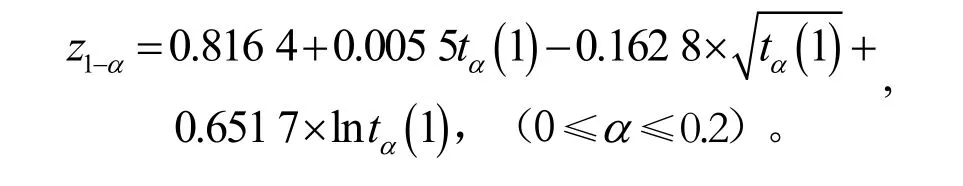
這個定理為建立分布t(1)、χ2(1)、F(1,1)和N(0,1)的分位數之間的聯系起到了“橋梁”式的作用。

用tα(1) = cot(πα)代入，就可得到得下面的結果。

定理2: 分布N(0,1)分位數的一個計算公式為：

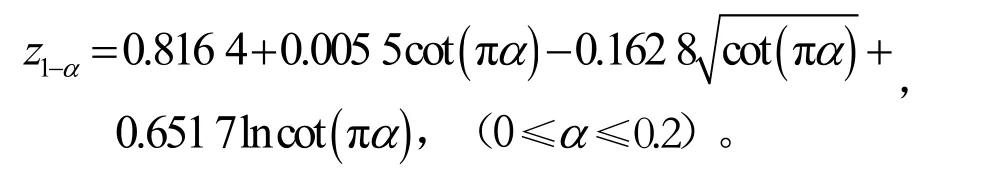
我們知道在可靠性統計分析中涉及分位數的α通常接近于 0或 1，當接近于 1時，可用zα=z1-α計算。

本公式的計算誤差如何？將在下一節加以說明。

定理3的結果由1.2節中的結果結合應用定理2即可得到。

2 數值比較

下面用列表形式給出分別用查表和定理 2計算得到的一些標準正態分布分位數數值（見表1）。

表1 查表和計算得到的正態分布分位數數值比較Table 1 Comparison of the two quartile values between lookup table and calculation

由表1結果顯示，此法可應用于可靠性統計分析實踐。與已有的、公認為較好的標準正態分布分位數的近似計算公式相比較，本文提出的新的近似計算公式雖然誤差大了一些，但計算卻更為簡便，只需要用小計算器依次算就可獲得結果。另外，本文提出的應用回歸分析方法來處理分位數關系的方法，也為其他分位數關系和計算的進一步研究提供了新途徑，具有借鑒意義。

3 應用舉例

例：某航天產品配件的結構強度可認為服從正態分布，今從產品中隨機抽取8件檢查其強度，得數據如下：11.9、9.9、8.7、12.2、9.0、10.1、11.0、10.6，試求該產品配件的結構強度的變差系數CV置信水平為93%的置信上限。

解：文獻[1]給出了當樣本容量n=2k(偶數)時，計算正態變差系數CV置信水平為1-α的置信上限公式：

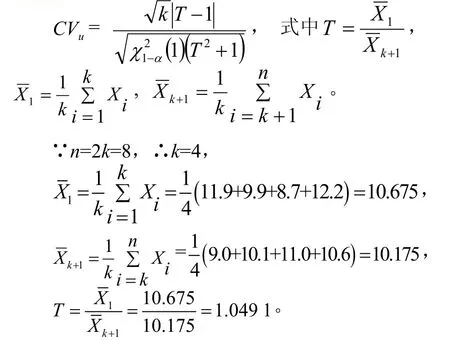
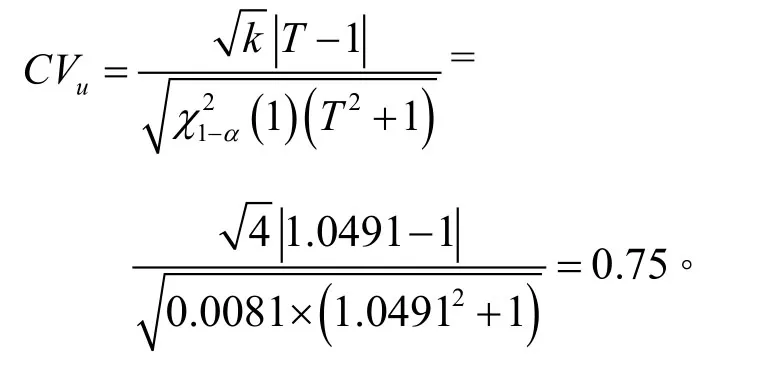
4 結論

本文給出了分布t(1)、χ2(1)、F(1,1)和N(0,1)的分位數之間的關系及一些簡單易用的計算公式，使原從表上直接查不到的一些結果可以通過間接查表方法得到；而有的原要查表的可以不用查表直接計算得到。因此，為文獻[1]、[2]等研究成果的應用提供了方便。

（References）

[1]孫祝嶺.正態分布變差系數的置信區間[J].兵工學報,2009, 30(7)： 911-914

[2]孫祝嶺.環境因子的非參數置信限[J].航天控制, 2009,27(5)： 102-105

[3]高惠璇.統計計算[M].北京大學出版社, 1995

[4]肖云茹.概率統計計算方法[M].天津： 南開大學出版社, 1994

[5]孫祝嶺, 徐曉嶺.數理統計[M].北京： 高等教育出版社, 2009