路面破碎機電液系統的自適應反推滑模控制

張平均 蔣新華

1．中南大學，長沙，410083 2．福建工程學院，福州，350108

0 引言

共振式混凝土路面破碎機［1］是一種新型的路面整改用工程機械，其行走機構采用液壓比例泵控馬達系統。電液比例系統［1－2］動態特性具有較強的非線性，且存在不確定性的模型參數和負載擾動，如壓力損失、閥的非線性特性等。同時行走機構本身和作業路面的參數也存在著較大的變化，如輪緣半徑的變化、路面坡度、材質和發動機速度的變化等。液壓行走系統的結構和參數特征，對行走速度控制的穩態精度、動態特性造成較大的影響。

Lyapunov函數在非線性系統的自適應控制設計中具有重要的作用，但如何構造Lyapunov函數需要理論的支持，而自適應反推法［3－5］提供了一種較為簡便的結構化、系統化方法，當干擾或不確定性不滿足匹配條件時，具有明顯的優越性。滑模控制方法［6－9］對系統數學模型精確度要求不高，算法簡單，對系統參數攝動和外部擾動具有較好的魯棒性等優點。自適應反推法和滑模控制方法之間的結合在非線性不確定控制系統中得到了應用研究［10－13］。

本文針對共振式混凝土路面破碎機行走機構液壓系統的參數不確定性，采用基于自適應反推滑模的控制策略，從而保證系統控制的穩定性和高精度的速度跟蹤特性。

1 路面破碎機行走機構的模型

路面破碎機行走機構是由一個行走泵驅動兩個行走馬達，再分別經減速機構驅動兩個后輪而工作的。通過速度踏板實現行走泵排量的電比例控制，兩行走馬達排量根據負荷調整，分別由各自的電磁閥進行開關量控制，使馬達排量達到最大或最小，從而實現對設備的行走速度進行控制。

行走機構的比例變量泵控馬達系統由多個液壓元件組成，可以分解為比例閥控制、泵變量機構、泵控馬達速度控制組合和機械傳動行走控制組合等部分，見圖1。其中泵控馬達組合的動態方程是建立在變量泵和馬達流量平衡以及馬達和負載轉矩平衡方程的基礎上的，在忽略馬達和負載之間連接剛度的情況下，建立系統模型如下：

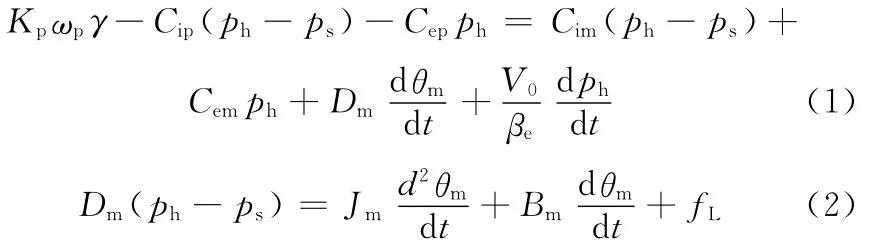
式中，Kp為變量泵的排量梯度，m3／rad；ωp為變量泵的轉速，rad／s；γ為變量泵斜盤傾角，rad；Cip、Cep分別為變量泵的內外泄漏系數，m5／（N·s）；Cim、Cem分別為馬達的內外泄漏系數，m5／（N·s）；ph、ps分別為高低壓腔側壓力，Pa；Dm為馬達排量，m3／rad；θm為行走馬達軸轉角，rad；V0為泵和馬達工作腔以及連接管道的總容積，m3；βe為液壓回路綜合彈性模量，N／m3；Jm為折算到行走馬達軸上的總轉動慣量，kg·m2；Bm為折算到馬達軸上的總黏性阻尼系數，N／（m／s）；fL為作用行走馬達軸上的總不確定性項，它包括了外負載轉矩及負載擾動等的不確定性擾動。

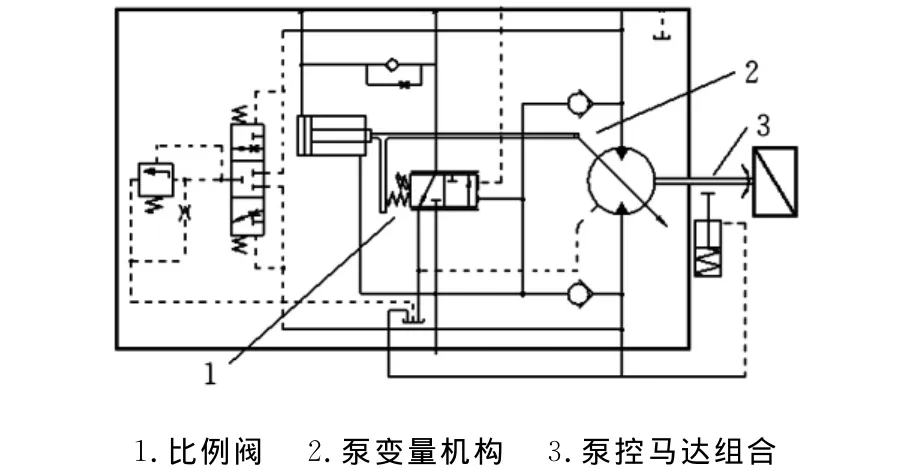
圖1 破碎機行走系統液壓原理圖

比例泵控制組合包括了電比例方向控制閥和閥控液壓缸的泵斜盤傾角調節結構，在忽略閥的頻率特性情況下，等效為

式中，u為比例閥的控制輸入信號；xv為比例閥閥芯位移，m；Ka為比例放大器增益；Kbv為比例閥的增益系數；Kγ為變量泵斜盤傾角系數；Kq為比例閥在穩態工作點附近的流量增益，m3／s；L為變量活塞油缸施力點與斜盤鉸接點間的距離，m。

行走機械傳動控制組合實現角速度到直線速度的轉換和動力傳遞，破碎機車輪半徑為0．7225m，速度檢測采用75脈沖／轉的旋轉編碼器，定義

式中，v為后輪行走速度，m／min；Kv為速度反饋回路增益；θ為后輪軸旋轉角位移，rad。

基于式（1）～ 式（5），取狀態變量x1＝v、x2＝v·，則系統的狀態空間模型為

式中，ωm為液壓固有頻率；ξm為阻尼比；Ctp為泵泄漏系數；Ctm為馬達泄漏系數；Jt為折算到測量端的總轉動慣量，kg·m2。

本文的研究著重于泵控馬達速度控制系統參數中的不確定性，由于系統溫度、工作油壓等的不同，Ct、βe及Bm等均是變化的，同時ωm、ξm明顯為非線性的，因此模型中定義α1、α2、α3為作用在各環節上的不確定性參數項。在實際系統中，可以認為這些不確定性項是有界的。

2 自適應反推滑模控制器設計

2.1 自適應反推滑模控制律的設計

自適應反推設計方法是將復雜的非線性系統分解成不超過系統階數的子系統，然后為每個子系統分別設計Lyapunov函數和中間虛擬控制量，一直后推到系統的實際控制信號，從而完成整個控制器的設計，其最大優點是最終得到的控制肯定可以保證整個系統的穩定。

系統的控制目標是馬達旋轉速度跟蹤，定義各步的跟蹤誤差為e1＝v－vr，其中，vr為第一步的期望值。為了使速度跟蹤誤差趨于零，定義第一步的Lyapunov函數為

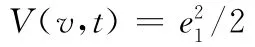
對其求導得

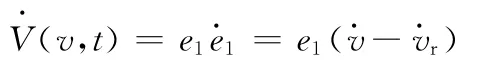
定義第二步的Lyapunov函數為

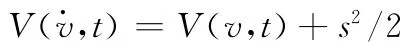
其中，s為滑模控制的切換函數，定義s＝c1e1＋e2，其中常數c1＞0，且

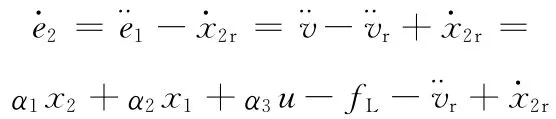
對V2求導，代入s·和e·2·，有

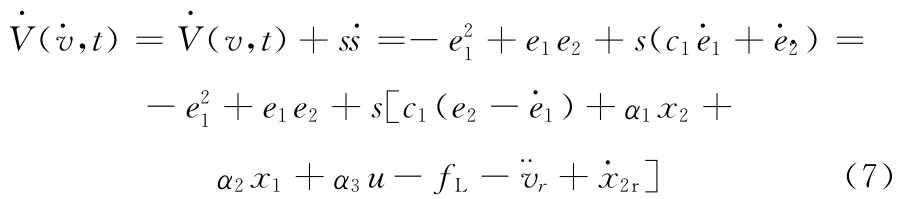
對于系統中的不確定性參數，可以采用取其上界或平均值的方法設計反推滑模控制器為

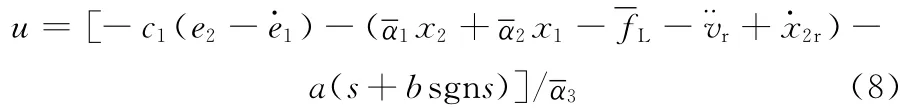
其中，u為加在比例泵控制組合上的實際控制信號；a、b均為控制器仿真參數，a＞0、b＞0；α1、α2、α3、fL均為相應的平均值，可由其上下界確定。實際應用中的滑模控制系統參數的不確定性和非線性等因素影響，使得滑動模態產生高頻抖振，高頻抖振可能激發系統未建模部分的強烈振蕩，出現超調過大、過渡過程延長，甚至出現不穩定狀態，且靜態指標也會降低，抖振問題己成為滑模變結構控制在工程應用中的突出障礙。如何消除抖振而又不失強魯棒性，仍是滑模變結構控制必須解決的首要問題，下面采用自適應算法對前面定義的不確定參數項進行實時估計，以提高參數的適用性能。

2.2 穩定性分析

定義Lyapunov函數為

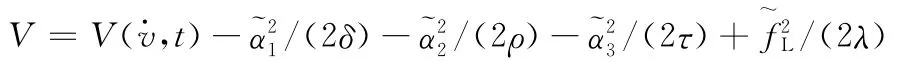
估計誤差分別定義為

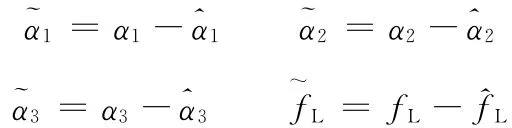
對其求導：

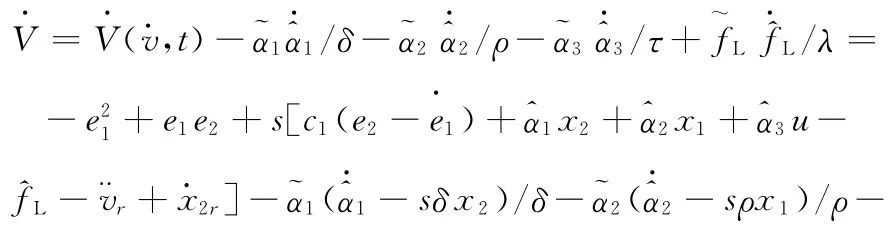
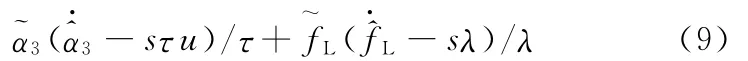
式（8）可以重寫為

設計自適應律為

將式（10）、式（11）代入式（9）得

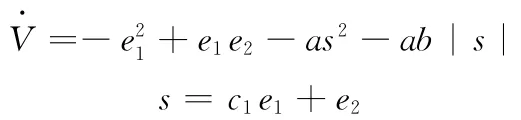
定義

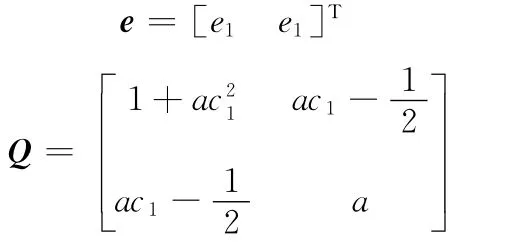
3 仿真和實驗結果

根據前面推導出的系統模型和控制策略，結合路面破碎機液壓回路的設備選型，確定其參數的標稱值如下：V0＝5．0×10－4m3、Ct＝2×10－10m5／（N·s）、Dm＝ 5．5×10－6m3／rad、βe＝ 2×107N／m3，Jt＝0．05kg·m2，Bm＝6．8×10－5N／（m／s），ph＝30MPa，ωm＝0．45，ξm＝232，Ke＝3．24，Kf＝3．11，α1＝22，α2＝40，α3＝3，fL＝57。

在MATLAB6．5軟件環境下對該控制系統進行了仿真實驗［14］，為了模擬參數的不確定性，選取fL＝57sin6t，采樣周期為0．001s。控制器仿真參數a＝12，b＝20，c1＝1．1，δ＝3，ρ＝15，τ＝18，λ＝15。仿真結果如圖2和圖3所示。

根據圖2的控制器輸出us比較分析，采用自適應反推滑模控制方法時，經過一段時間調節后，控制量的顫振幅度較小，說明控制策略能根據不確定性參數項的估計值自動調節滑模校正項的控制增益，有效地抑制了控制量的顫振強度。這主要在于系統的自適應律可有效抑制參數的不確定性。

圖2 兩種情況下us的變化曲線

圖3 速度方波響應曲線

圖3 為幅值等于15m／min的方波控制下的系統速度響應，顯示出具有較好的性能指標，速度動態升、降曲線符合液壓系統要求，且超調較小，可以提高液壓元件的安全性，穩態精度較高，可以在此基礎上提高整車的節能性能。

根據圖4分析，在速度的上下調節時，速度的波動曲線可以滿足系統的運行要求。

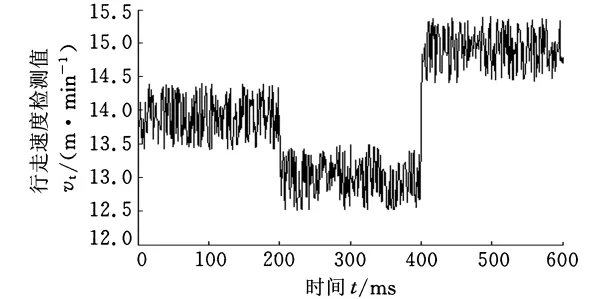
圖4 行走速度調節曲線

4 結語

本文針對路面破碎機行走機構的速度控制問題，采用了自適應反推滑模控制方法，對于參數擾動及負載波動，具有較好的動態響應性能，且控制算法簡單，便于工程機械車載控制系統的應用。

［1］ Eugeniusz B，Miroslaw C，Witold G．Load－independent Control of a Hydraulic Excavator［J］．Automation in Construction，2003，12（3）：245－248．

［2］ Pommier V，Sabatier J，Lanusse P，et al．Crone Control of a Nonlinear Hydraulic Actuator［J］．Control Engineering Practice，2002，10（4）：391－402．

［3］ Guang L，Amir K．Robust Control of a Hydraulically Driven Flexible Arm Using Backstepping Technique［J］．Journal of Sound and Vibration，2004，208（3／5）：759－775．

［4］ Kim K，Kim Y．Robust Backstepping Control for Slew Maneuver Using Nonlinear Tracking Function［J］．IEEE Trans．on Automatic Control，2003，11（6）：822－829．

［5］ 董文瀚，孫秀霞，林巖．反推自適應控制的發展及應用［J］．控制與決策，2006，21（10）：1081－1087．

［6］ Edwards C．A Practical Method for the Design of Sliding Mode Controllers Using Linear Matrix Inequalities［J］．Automatica，2004，40（10）：1761－1769．

［7］ Barrolini G，Pisano A，Punta E，et al．A Survey of Applications of Second－order Sliding Mode Control to Mechanical Systems［J］．International Journal of Control，2003，76（9）：875－892．

［8］ 徐東光，吳博，吳盛霖，等．基于模糊調節的Stewart平臺積分滑模變結構控制器的設計［J］．中國機械工程，2008，19（4）：402－405．

［9］ 段鎖林，安高成，薛軍娥，等．電液伺服力控系統的自適應滑模控制［J］．機械工程學報，2002，38（5）：109－113．

［10］ 安樹．反演滑模控制在BLDCM伺服系統中的應用［J］．機械工程與自動化，2008，151（6）：161－163．

［11］ 鄭劍飛，馮勇，鄭雪梅．不確定非線性系統的自適應反演終端滑模控制［J］．控制理論與應用，2009，26（4）：410－414．

［12］ Ali J，Alan S，Zinober I，et al．Adaptive Sliding Mode Backstepping Control of Nonlinear Systems with Unmatched Uncertainty［J］．Asian Journal of Control，2004，6（4）：447－453．

［13］ 李俊，徐德民．電機驅動機械手的自適應反演變結構控制［J］．機械科學與技術，2001，20（4）：528－530．

［14］ 劉金琨．滑模變結構控制 MATLAB仿真［M］．北京：清華大學出版社，2005．