考慮缺貨風險的具有模糊隨機需求的訂貨量模型

李 麗，劉 杰

(1.同濟大學 經濟與管理學院，上海 201804；2.德州學院 計算機系，山東 德州 253023；3.復旦大學 管理學院，上海 200433)

0 引言

供應鏈上的很多制造型企業為客戶提供準時化（Just In Time，JIT）供應服務。在市場需求不確定情況下,由于制造業生產周期長，供應商為提供JIT服務，需要保持很高的庫存水平。然而，企業由于庫存成本有限，難以維持高的庫存水平，因而常常面臨缺貨的風險。傳統的EOQ模型不考慮缺貨的風險，因而不能很好地解決現實中的需求不確定環境中的訂貨量決策問題。

有些情況下，供應鏈上的市場需求具有模糊隨機性。當市場需求被描述為隨機變量時，很多學者基于概率測度研究問題。而當需求為模糊變量時，學者們基于模糊數學體系中的可能性、必要性和可信性等測度（其中可信性測度被認為是與概率測度平行的概念[1]）研究問題。因此，在模糊隨機需求環境中，本文擬基于模糊隨機理論中的機會測度與模糊理論中的可信性測度方法探討庫存策略的訂貨量決策模型。Tan和Tang[2]基于可信性概念將CSL(Cycle Service Level,補給周期供給水平)定義為在一個補給周期中不出現貨物短缺的可信性。同樣地，本文基于模糊隨機機會測度方法表示補給周期供給水平，描述不發生缺貨的模糊隨機事件。

與Tan和Tang[2]的研究不同，本文假設提前期為固定值,提出模糊隨機需求的周期盤點庫存策略的訂貨量決策模型。針對管理者設置的不發生缺貨的置信水平，決策合理的訂貨量以最小化庫存成本，并通過計算示例分析對訂貨量的影響。

為方便表述，本文采用下列符號：

L——提前期；

T——檢查周期；

CSL——補給周期供給水平；

S——目標庫存水平；

I——當前周期檢查時的現有庫存；

Q——訂貨量；

h——單位產品的庫存持有費用；

s——單位產品的缺貨費用；

c1——訂貨費、生產準備費和配送費用；

B1——庫存管理每周期最大的預算費用；

B2——最大的存儲空間。

1 模糊隨機需求與不發生缺貨模糊隨機事件的數學描述

1.1 模糊隨機需求的數學描述及期望值的計算

本文利用模糊隨機變量刻畫具有模糊隨機性的市場需求。關于模糊隨機變量及可測性有多種定義，Puri M和Ralescue D[3]（1986）、Kruse R 和 Meyer K[4]（1987）以及 Liu Y和Liu B[5]（2003）根據各自理論和不同領域的要求，給出了不同的可測性，從而產生了不同的模糊隨機變量的數學定義及測度方法。本文主要利用Liu B和Liu Y[6]（2002）、Liu Y和Liu B[7]（2003）、Liu B[1]（2004）提出的模糊隨機變量的相關理論（定義、測度及運算方法）。

定義1[7]假設ξ是一個從概率空間（Ω，A，Pr）到模糊變量集合的函數。如果對于R上的任何Borel集B，Cr{ξ(ω)∈B}是ω的可測函數,則稱ξ為一個模糊隨機變量。

定義2[7]設f:Rn→R是一個可測函數，并且ξi為定義在概率空間(Ω，A，Pr)上的模糊隨機變量，i=1,2,…，n，則 ξ=f(ξ1,ξ2,…，ξn)是一個模糊隨機變量，定義為 ξ(ω)=f(ξ1(ω)，ξ2(ω)，…，ξn(ω))。

定理1[1]如果模糊變量ξ的隸屬函數為μ，則對實數集上任意的集合B，有下面的結論成立：

根據定理1，設ξ是隸屬函數為μ的模糊變量，x和r為實數。模糊事件ξ≤r的可信性為

例如，設 ξ為三角模糊變量(l1,l2,l3)，其中 l1、l2和 l3為清晰數，并且 l1＜l2＜l3，ξ的隸屬函數為

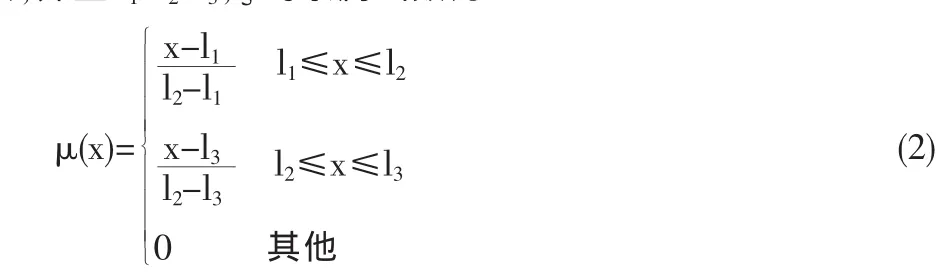
由⑴式可信性的公式得ξ≤r的可信性為：

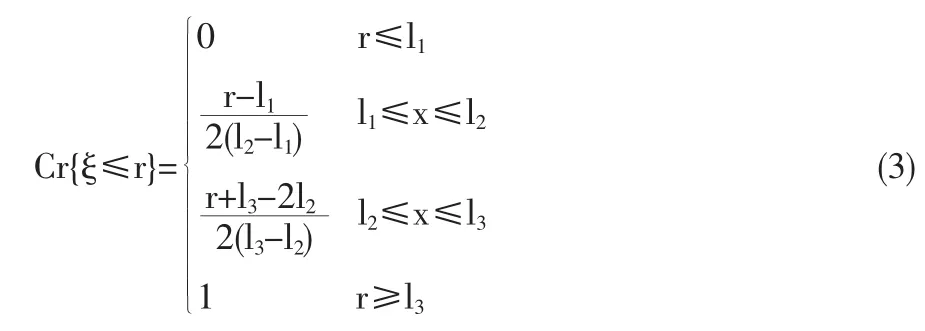
Cr{ξ≤l1}＜Cr{ξ≤l2}時意味著模糊事件{ξ≤l2}比模糊事件{ξ≤l1}發生的機會大。Cr{ξ≤r}=1當且僅當預期事件 100%發生。基于可信性測度，Liu and Liu[6]定義了的期望值，如定義3。

定義3[6]設ξ為可能性空間(Θ,P(Θ),Pos)上的模糊變量，ξ的隸屬函數為μ,r為實數。則稱

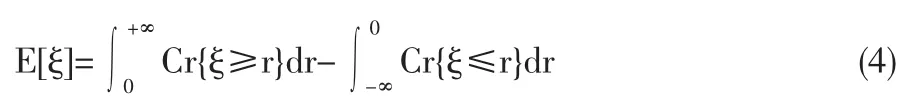
為模糊變量ξ的期望值（為了避免出現∞-∞情形，要求上式右端中兩個積分至少有一個有限）。尤其是，如果ξ是一個正的模糊變量，那么

定義4[6]設ξ為可能性空間(θ,p(θ),pos)上的一個模糊變量，f為 R→R 上的函數。 則 f(ξ)的期望值 E[f(ξ)]被定義為只要兩個積分中至少有一個是有限的。

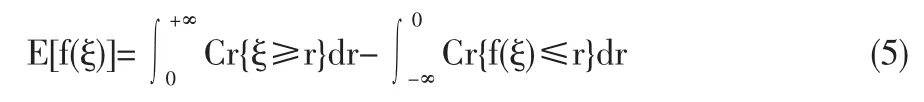
在現實的不確定市場環境中，企業根據已有的各種信息描述未來不確定的需求以安排其生產計劃。設需求D～是一個從概率空間(Ω,A,Pr)到模糊變量構成的集合的函數。Ω=(ω1,w2,…，wn)，d～1，d～2，…，d～n為正的模糊變量。 根據定義 1，定義需求D～為以下形式的模糊隨機變量

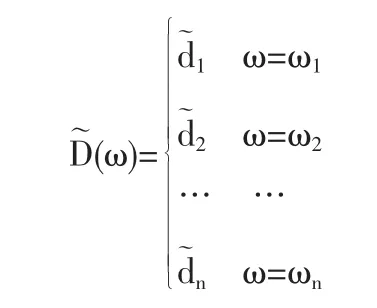
假設不確定市場環境下存在如市場需求比預計的需求量減少、與預計的需求量相當、比預計的需求量增多等種隨機市場情形，用ωi表示不確定市場環境下的第種隨機市場情形，用pi(i=1,2,…，n)表示i種市場情形發生的概率。本文將需求表示為如下形式：

步驟 1：令 e=0。

步驟2：根據隨機市場情形因素ω的概率分布p{ωi}=pi，隨機抽取 ωi={ω1，ω2，…，ωM}∈Ω，得到

步驟3：利用模糊隨機模擬計算模糊需求期望值。

⑴令k=0。

⑵利用計算機隨機數產生技術產生隨機數，服從均勻分布，令Q=ai=r(ci-ai)

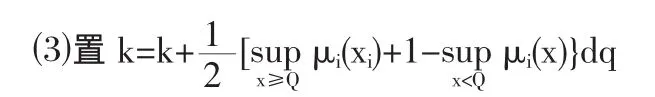
1.2 不發生缺貨模糊隨機事件的數學描述

對不發生缺貨這個事件的描述，在隨機的環境中使用概率測度或可能性測度。在模糊環境中，使用可信性測度。本文在模糊隨機環境中，使用平均機會測度。平均機會測度是一個模糊隨機事件的測度，描述了模糊隨機事件發生的平均機會。在文獻[6][9]中定義并應用了平均機會。

定義 5[10][11]設 ξ=(ξ1,ξ2,…，ξn)為定義在概率空間(0,A,Pr)上的模糊隨機向量，f:Rn→Rm為可測函數，則稱

Ch{f{ξ}≤0}(α)=sup{β|Pr{ω∈Ω|Cr{f(ξ(w))≤0}≥β}≥α}(9)為模糊隨機事件f(ξ)≤0的本原機會，它是從(0,1]到[0,1]的函數。

定義 6[12]設 ξ=(ξ1,ξ2,…，ξm)是一個定義在概率空間(0,A,Pr)上的n維模糊隨機向量，函數f:Rn→Rm是一個可測函數，則稱為模糊隨機事件{f{ξ}≤0}的平均機會。

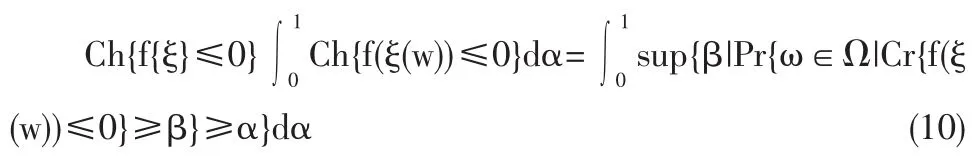
在一個補給周期中,不出現貨物短缺模糊隨機事件的平均機會測度用CSL來表示。在采用(T,S)策略的企業中,倉儲管理者在給定的CSL下確定的訂貨量應滿足以下條件：

CSL=Ch{一個周期內的市場需求D～≤庫存水平S+期望缺貨量}

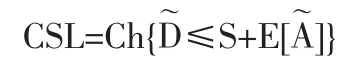
令 s=Q+I，則

管理者提供一個CSL的置信水平以表明管理者對不發生潛在缺貨事件的平均機會的置信水平。本文給出缺貨風險下庫存控制的衡量標準：SCL為管理者的庫存管理方案X的置信水平。如果

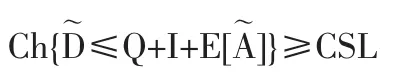
即不發生缺貨的平均機會測度大于管理者給出的置信水平，則方案X是安全的。現實世界中，如果CSL太低，將會降低供應鏈企業的競爭力。

2 考慮缺貨風險的具有模糊隨機需求的訂貨量模型

本文假設企業生產一種類型的產品，單周期、單倉庫。假設市場需求連續，每單位時間內的需求量不確定。在(T,S)策略下，企業按照預定的間隔T定期檢查庫存，并提出訂貨，將庫存補充到目標庫存量S。(T,S)控制策略下的存儲狀態變化如圖1所示。

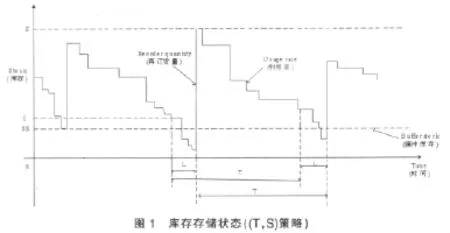
則一個周期內的缺貨量為

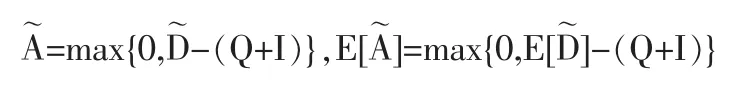
設c1為訂貨費、生產準備費和配送費等費用的和，定義一個周期內的模糊隨機總費用為則

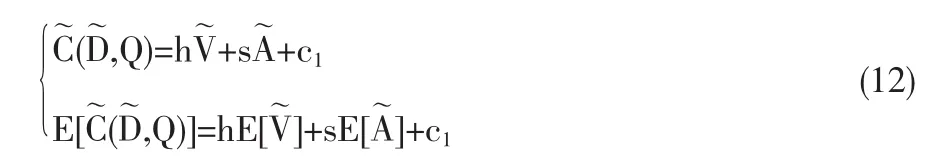
即

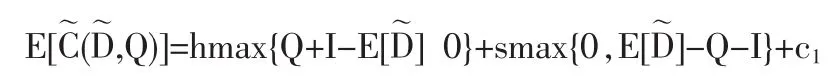
模糊隨機市場需求下，管理者在不發生缺貨置信水平、預算費用和庫存空間的約束下決策最優訂貨量以最小化庫存管理的費用期望值。模型的目標函數為：

不發生缺貨置信水平的約束為：

對于不允許缺貨的模型，一般假設CSL的值很高。

如果管理者希望一個周期的庫存管理費用不超過預算費用，則關于預算資金的約束為：

其中，B1表示庫存管理每周期最大的預算資金。

如果倉庫的最大空間容量為B2，則關于庫存空間的約束為：

綜合(13)～(16)式，模型為：

3 基于模糊隨機模擬的智能算法

得到機會函數的精確值是非常困難的，必須借助于模糊隨機模擬。本文整合模糊隨機模擬和遺傳算法求解一般情況下的模型問題。算法中，先用模糊隨機模擬檢查約束的可行性并計算目標函數值，然后，模糊隨機模擬與遺傳算法（Genetic Algorithm，GA）相結合解模糊隨機模型。

3.1 模糊隨機模擬

假設用Q表示決策變量。為求解提出的模型問題，先處理下列兩種類型的不確定函數。第一種類型的不確定函數是

關于約束的不確定函數為以下形式：

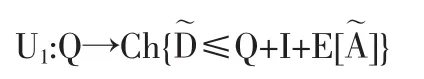
令

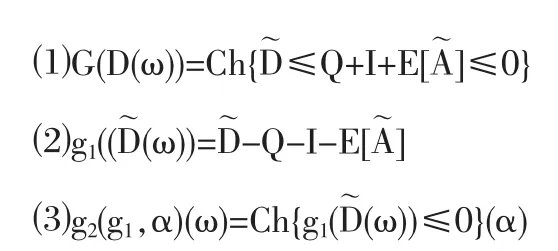
則

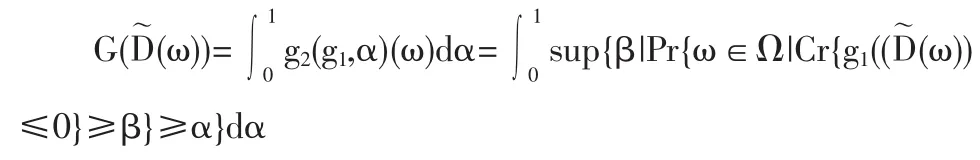
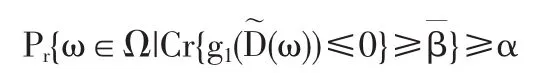
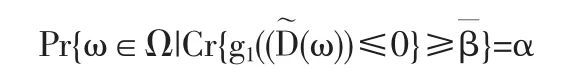
因此，估計 g2(g1,α)(ω)值的步驟如下。

步驟1：根據概率分布pr，從樣本空間Ω中抽取樣本ω1,ω2,…，ωN。

⑴令j=1。

⑶置 xj和 μ(xj)。

⑷j←j+1，如果j≤N，執行步驟⑵；否則，執行步驟⑸。

步驟3：置N'為αN的整數部分。

步驟 4：返回序列{β1,β2,…，βN}中第 N'個最大的元素。

估計平均機會(ω)dα 值）的步驟如下。

步驟1：隨機抽取N個獨立的服從u(0,1)的隨機數αi。

3.1.2 目標函數

步驟 1：令 E=0。

步驟2：根據概率分布Pr，從樣本空間Ω中隨機抽取樣本 ωi。

F（yi）=yj=hmax{Q+I-xj,0}+smax{0,xj-Q-I}+c1

⑵計算,a=F(y1)∧F(y2)∧…∧F（yN），b=F(y1)∨F(y2)∨…∨F（yN）。

⑶從[a,b]中隨機產生z，z為任意實數。

⑹重復⑶～⑸步N次。

步驟5：重復步驟2至步驟3共N次。

步驟4：返回γ的值作為

3.2 基于模糊隨機模擬的智能算法設計

模型求解過程如圖2所示。

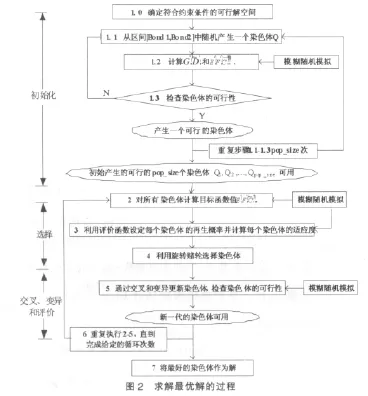
3.2.1 初始化

由約束函數1+Q≤B2和Q≥0得到可行集的區間[Bond1,Bond2]。從區間[Bond1,Bond2]中隨機產生一個染色體Q，對于CSL，使用模糊隨機模擬檢驗染色體的可行性。如果成立，并且也成立，這里,染色體是可行的。保留此染色體。否則，隨機產生另一個染色體Q。繼續此初始化過程直到得到可行的pop_size個染色體。

3.2.2 選擇過程

通過旋轉賭輪選擇染色體，使得好的染色體有更多的機會產生后代。

在旋轉賭輪之前，通過模糊隨機模擬計算目標函數值 ，并按照目標函數值從好到壞按照Q1,Q2,…，Qpop-size的順序重排染色體。對模型⒄，期望值越低，染色體越好。利用基于序的評價函數對每一染色體Q計算再生概率。給出參數β∈(0,1)，基于序的評價函數 eval(Q)為 eval(Qi)=β(1-β)i-1,i=1,2,…pop-size，i=1意味著是最好的染色體，i=pop-size是最壞的染色體Qi。對于每個染色體，按以下公式計算累積概率：

p0=0，pi=eval(Q1)+eval(Q2)+…+eval(Qi)（i=1,2,…，pop-size）

從區間(0,Ppop-size]中隨機產生一個實數r,r落在(pi-1,pi]中的概率就是第i個染色體被選中的概率。概率與染色體的適應度成比例。

旋轉賭輪。隨機產生一個(0,Ppop-size]中的實數r。如果Pi-1＜r≤Pi，選擇第 i個染色體 Qi(1≤i≤pop-size)。 重復這兩步pop_size次，選擇出pop_size個染色體。

3.2.3 交叉操作

預先確定參數pc作為遺傳系統的交叉概率。當第i次從[0,1]中隨機產生的實數r小于pc時，選擇染色體Qi作為父代。

首先，從開區間（0，1）中產生一個隨機數e。然后通過交叉操作產生兩個新染色體X和Y。如果兩個子染色體可行，則用子染色體替代父染色體。否則，保留其中可行的染色體（如果存在的話），然后重新產生一個隨機數e進行交叉操作，直到獲得兩個可行的子染色體或完成給定次數的循環為止。僅用可行的子染色體替代父染色體。

3.2.4 變異操作

預先設置一個概率參數pm對選擇出來的父代染色體進行變異。當第i次選擇的從區間[0,1]隨機產生的實數r小于pm時，將染色體Qi作為父染色體。令Q表示一個被選擇的父染色體，以下列方式進行變異。

隨機在(-1,1)中選擇一個變異方向D。令M為一個合適大的正數。如果Q+MD可行，用這個新染色體作為子染色體。否則，將M作為0和M之間的一個隨機數，這樣又得到了一個新的染色體，再檢驗其可行性，直到新的染色體可行為止。如果在一個預先設定的迭代次數內不能發現一個可行解，令M=0。任何情況下，僅用Q=Q+MD替代父染色體Q。

進行選擇、交叉和變異后，得到新的染色體，準備下一輪的進化。對上述步驟經過給定的循環次數之后，算法終止。

4 數值算例

為了驗證優化思想并測試設計的算法的有效性，本文給出一個數值例子。

例1.假設VMI模式下，供應商估計的下游企業的需求為

表1 VMI庫存系統參數值

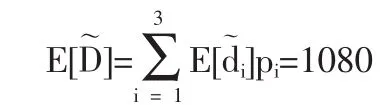
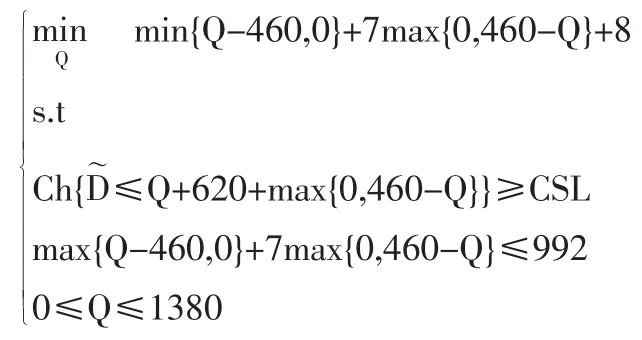
設定算法中的 pop-size=50,β=0.05,pc=0.3,pm=0.2，遺傳迭代1000次，運行智能算法。對給定的CSL的置信水平，求得模型⒄的結果如表2所示，相應的最小期望費用也如表2所示。為了滿足條件約束并最小化訂貨量選擇所得到的期望費用，管理者應該按表2決策訂貨量。

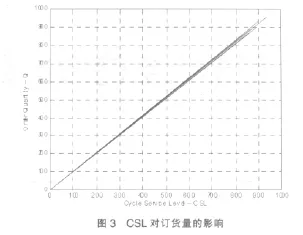
圖3表明CSL對訂貨量的影響，結果符合真實的決策行為。

為了進一步測試設計的算法的效率，對GA中不同的參數值做了更多的試驗。結果見表3。按照公式“相對誤差=（(實際期望值-最優期望值)/最優期望值）×100%”，計算出相對誤差，其中最優期望值是所有計算出的最優目標值中最小的。對比目標函數值的結果，從表3可以看出當設置不同的參數值時相對誤差不超過0.003%，這表明對設置的參數來說，設計的算法是魯棒的，對解模型問題⒄來說，算法是有效的。

5 結論

在模糊隨機環境中，市場需求是不確定的。由于庫存成本等條件的限制，企業常常面臨缺貨的風險。基于模糊隨機事件的機會測度，本文提出不發生缺貨的模糊隨機事件的測度方法。提出當市場需求被描述為模糊隨機變量時，不發生缺貨置信水平、預算資金及庫存空間約束的訂貨量問題的模型。此外，設計基于模糊隨機模擬的智能算法來解一般的模型問題。數值算例的結果和實驗表明，對于解優化問題，設計的算法對于設定的參數是魯棒的和有效的，在提出的算法中，解的時間主要花在模糊隨機模擬上。如果能用一個解析方法來化簡模型，能大大縮短解的時間。

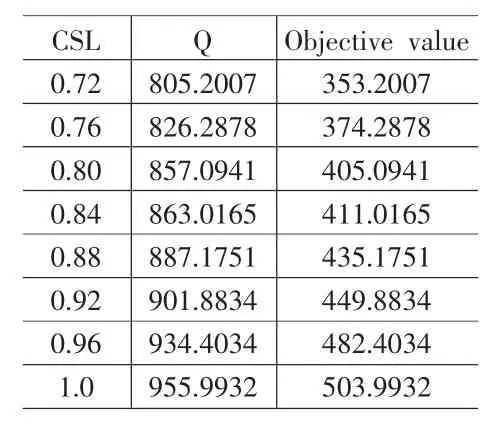
表2 例1的解的比較

表3 例1解的比較(pop-size,β=0.05,Pc=0.3,Pm=0.2)

[1]Liu B.Uncertainty Theory:An Introduction to Its Axiomatic Foundations[M].Berlin:Springer-Verlag,2004.

[2]Tan M,Tang X.The Further Study of Safety Stock under Uncertain Environment[J].Fuzzy Optimal Decision Making,2006,(5).

[3]Puri M,Ralescu D.Fuzzy Random Variables[J].Journal of Mathematical Analysis and Applications,1986,114.

[4]Kruse R,Meyer K.Statistics with Vague Data[M].Dordrecht:D.Reidel Publishing Company,1987.

[5]Liu Y,Liu B.A Class of Fuzzy Random Optimization:Expected Value Models[J].Information Sciences,2003,155.

[6]Liu B,Liu Y.Expected Value of Fuzzy Variables and Fuzzy Expected Value Models[J].IEEE Transactions on Fuzzy Systems,2002,10(4).

[7]Liu Y,Liu B.Fuzzy Random Variables:A Scalar Expected Value Operator[J].Fuzzy Optimization and Decision Making,2003,2(2).

[8]于春云,趙希男,彭艷東等.模糊隨機需求模式下的擴展報童模型與求解算法[J].系統工程,2006,24(9).

[9]Liu B.A Survey of Credibility Theory[J].Fuzzy Optimization and Decision Making,2006,5.

[10]Liu B.Fuzzy Random Chance-Constrained Programming[J].IEEE Transactions on Fuzzy Systems,2001,9(5).

[11]Gao J,Liu B.New Primitive Chance Measures of Fuzzy Random Event[J].International Journal of Fuzzy Systems,2001,3(4).

[12]Liu Y,Liu B.On Minimum-risk Problems in Fuzzy Random Decision Systems[J].Computers&Operations Research,2005,32.