GPS動態測量中系統誤差的分離方法

湯 云,金元剛,付 平

(1.解放軍92941部隊,遼寧葫蘆島125001;2.中海油能源發展有限公司,天津300450)

0 引 言

在動態測量數據處理中,系統誤差是很棘手的問題,研究系統誤差的有效處理方法正受到越來越多的關注。系統誤差的特性非常復雜,既具有延續性,又有偶然性,因而很難用統一的、確定性的模型來準確描述它。就GPS動態測量來說,信號受到多種誤差源的誤差干擾,有的誤差(例如電離層折射影響)可以利用雙頻接收機的方式得到較好補償,而多路徑影響卻很難找到有效的改正模型。系統誤差雖經部分模型改正,或差分改正,仍有部分殘余留在觀測量中,或多或少影響到定位結果的精度[1]。

在很多GPS定位技術的文獻資料上,定位誤差都按如下方法進行估計[2]

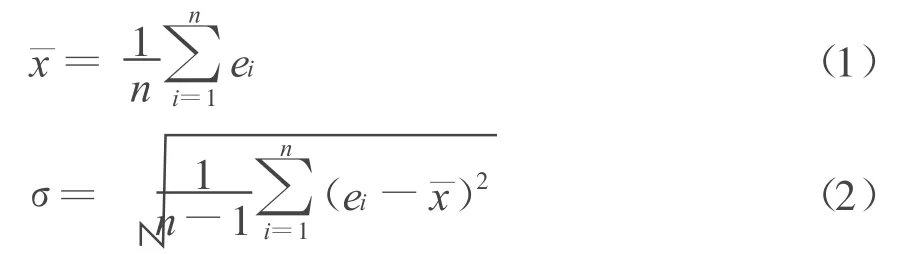
式中:ei是第i次采樣的誤差;n為樣本容量;ˉx為系統誤差;σ為標準差。

上述誤差估計方法的誤差模型是用隨機變量來描述的。對于GPS靜態定位或靜態測量時是正確的,但將這種方法用于GPS動態定位或動態測量中一般是不正確的,因為只有當系統誤差是常量時,該方法才可適用。而實際上GPS動態測量的系統誤差一般并不是常量,其誤差曲線并不水平。對于GPS動態測量系統的誤差估計,應力求提高誤差估計結果的精度或可信度。為了科學客觀地評定一個GPS動態測量系統的性能,有必要研究適合GPS動態測量的數據處理方法。

1 GPS動態測量的誤差特性

GPS動態測量的誤差是隨機過程或經采樣以后形成的隨機序列,當用戶臺處于動態時,這是很顯然的。在GPS動態測量系統的鑒定試驗中,可以采用靜態目標試驗動態性能,這種方法盡管是采用靜止目標,但本質上不同于靜態測量。因為噪聲引起的誤差、傳播介質產生的誤差(包括電離層、對流層折射和多徑效應引起的誤差)、衛星鐘差、衛星星歷誤差等經差分后的殘余誤差都是隨機過程,采用單歷元解算,這種特性被保留下來并離散化為隨機時間序列。

GPS測量的誤差中,傳播介質產生的誤差、衛星鐘差、衛星星歷誤差等存在隨時間慢變的成分;不同歷元可能有不同導航衛星的信息參與運算,其DOP值一般情況下也是不同的,由此產生的誤差也是隨時間變化的;在載波相位差分定位中,周跳引起的誤差在不同歷元也是變化的。這些隨時間慢變的誤差成分形成了系統誤差,它們并不表現為常值,而是時間的隨機函數。除上述慢變成分外,它們的快變部分以及噪聲引起的誤差則成為噪聲狀態的隨機誤差部分。

GPS動態測量系統的誤差是由熱噪聲、量化噪聲、電離層和對流層折射產生的誤差、衛星鐘差、衛星星歷誤差、基準站誤差、模糊度解算誤差等許多誤差分量綜合的結果。在接收機和衛星系統正常工作的情況下,各種誤差對總誤差的影響都不顯著。根據中心極限定理,系統測量誤差的概率分布為正態分布。

綜合以上分析,GPS動態測量系統的動態測量誤差是非平穩的正態隨機序列。誤差的這一特性是研究數據處理方法的出發點。

2 處理方法的理論基礎

2.1 非平穩隨機過程誤差處理方法

動態測量誤差是非平穩的正態隨機過程或經采樣得到的隨機序列,用x(t)表示。其中有變化緩慢的誤差成分y(t)和快變的誤差成分η(t),即

式中:慢變誤差y(t)稱為系統誤差,而把零均值的η(t)稱作隨機誤差。

根據隨機過程的理論,估計動態測量誤差 x(t)的均值和方差需得到 x(t)在ti時刻的抽樣值x1(ti),x2(ti),…,xn(ti),它們是來自x(ti)的樣本點。其中xj(t)是指來自x(t)的第j個樣本記錄,對應于系統在相同狀態下(以保證它們來自同一過程x(t))所做的第j次試驗(第j航次、架次)。用隨機變量樣本值的統計方法(即式(1)和式(2))得到ti時刻的估計。對記錄的每一時刻都做如此處理,就可得到均值函數和方差函數[3]。

但是上述處理方法對GPS動態測量誤差估計存在很大困難。需要做許多次試驗才能保證誤差估計的精度。這多次試驗要保持系統狀態相同可以說是無法實現的。比如,不同次數的試驗要求跟蹤相同的衛星,要求DOP值相等,這些都是不可能的。因此動態誤差的估計需要另想辦法。

2.2 各態歷經隨機過程誤差處理方法

按照隨機過程理論,如果過程具有各態歷經性,則上述估計等價于對一個記錄的相應時間均值的估計,即可通過對一個記錄時間均值的計算得到x(t)的均值和方差的估計[4]。

經過論證有如下結論:對于只求正態隨機過程的一、二階矩,如果過程是平穩的,則具有各態歷經。但是如前所述x(t)一般并不平穩。

對于式(3)中的系統誤差y(t),并不同于雜亂無章的噪聲,它的出現具有一定規律性。只要試驗時間足夠長,即可用一個現實(一次試驗)數據得到。能否用時間均值作為動態誤差的估計,關鍵是看噪聲η(t)是否具有各態歷經。將x(t)中的系統誤差y(t)分離以后,所剩η(t)如果平穩,理論上就可用一個現實的數據完成誤差統計。

3 系統誤差分離

系統誤差是具有規律性的慢變誤差,可以用一個解析函數逼近。由函數逼近理論,如果函數 f(t)在區間[a,b]上連續,則在該區間上總可用一個代數多項式P(t)去一致逼近。用n階多項式a0P0(t)+a1P1(t)+…+anPn(t)作為系統誤差y(t)的模型,由此得

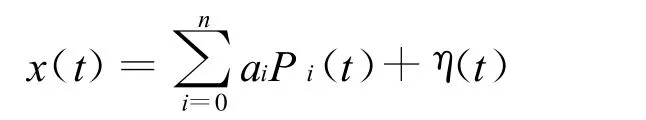
其離散序列為

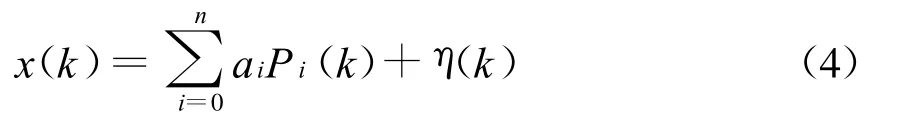
式中:k=1,2,…,N。N為序列長度。令

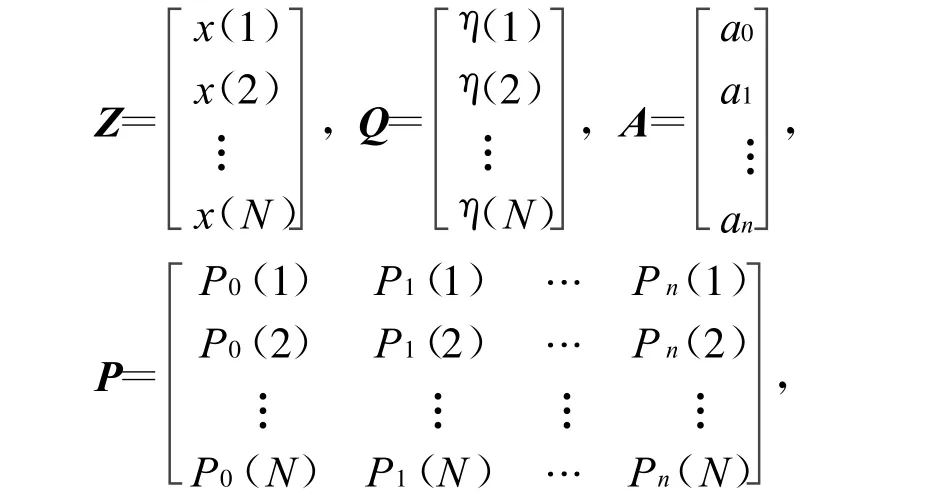
參數A的最優估計為

式中:R是Q的方差陣,或者是η(t)的相關函數陣。

假如η(t)二階平穩且不相關,則可令R-1=I,而實際上η(t)是相關的,并且有時是強相關,尤其在定位處理中采用了卡爾曼濾波后更是如此。為了避免計算R的困難,常用的方法是獨立抽樣。獨立抽樣的問題存在相關時間計算是否較為準確,而主要問題是獨立抽樣引起y(t)的失真。通過頻域研究發現獨立抽樣引起y(t)的失真幾乎是不可避免的,這種方法不能得到系統誤差的最優估計。

求A的最優估計可考慮如下算法

①令R=I,得到初始估計A0;

②用A0分離系統誤差,其殘差作為η(k),求方差陣R0。由于A0不是最優估計,R0只是R的初始估計;

③令R=R0,用式(5)估計A得到A1,A1是比A0更好的估計;

④用A1分離系統誤差后再次估計R得到R1,R1是比R0更好的估計;

⑤再令R=R1重新估計A,依此循環直到滿足計算精度。

這種方法實際上會產生很大的計算誤差。GPS動態測量系統采樣率一般不低于20 Hz,為了充分考核動態測量精度,一次試驗要連續記錄30 min以上,誤差序列將有幾萬組以上的采樣值。x(t)的方差陣將達幾萬階以上,很難保證其正定性。即使能保證正定,這樣高階矩陣的求逆要經過許多步的計算,使計算誤差大量累積。

通過研究和實際計算形成了求解系統誤差參數的如下方法。

零均值平穩隨機序列可用ARMA模型描述,而ARMA可用足夠高階的AR模型模擬,因此,零均值平穩隨機序列可用AR模型建模

式中:ε(k)為白噪聲;φ(B)為算子多項式

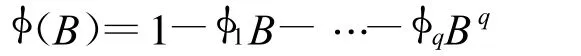
將式(6)代入誤差模型式(4),有

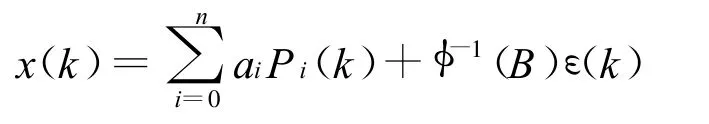
即

令

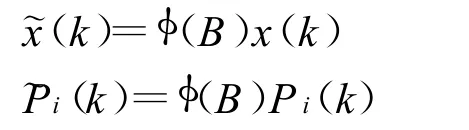
式(7)為

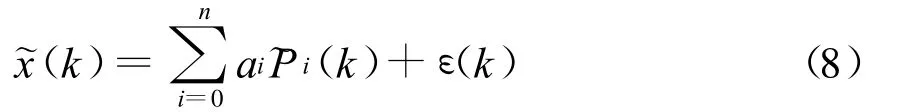
如果得到N+q個樣本值,有

式中:

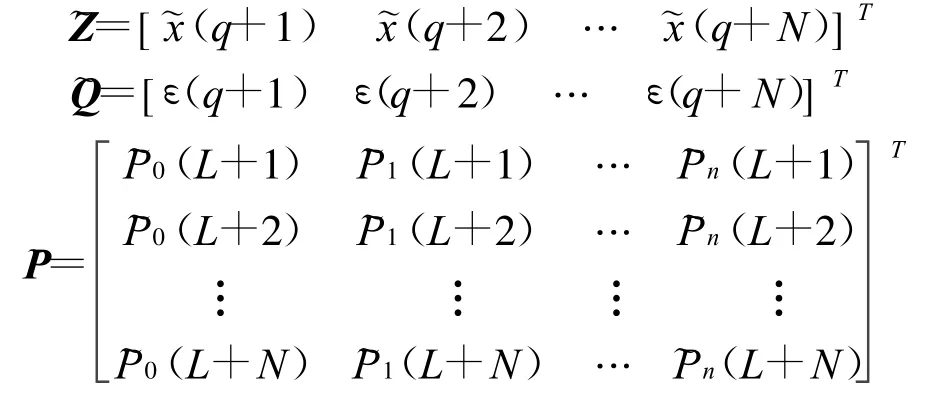
由于ε(k)是零均值白噪聲,因此ai的最優估計為

可以進一步推導出AR模型參數的估計

式中:Φ=[φ1 φ2 … φL]T,R(L)是L維隨機變量η(k)的方差陣,而 Σ(L)是L維隨機變量η(k)的協方差組成的列向量。

Φ還可用最小二乘估計得到

式中:

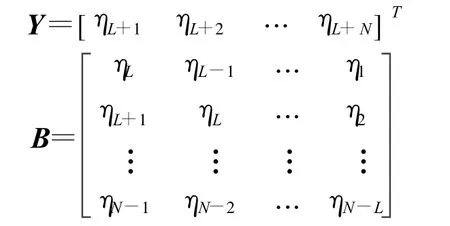
式(11)、式(12)中的R-1(L)和(BTB)-1都只是L階矩陣求逆,而L不會超過10,顯然比幾萬階矩陣求逆誤差小得多。

計算方法與前述逐次求R矩陣的方法相同。首先令φ(B)=1,得到初始估計A0,進而得到初始估計 Φ0。利用 Φ0重新計算得到A1和 Φ1,直至達到計算精度。

4 實測GPS數據誤差分析

為了驗證算法的有效性,采用2009年3月20日某無人機飛行記錄的GPS測量數據進行多項式擬合及誤差分離。無人機飛行了大約1 h,機載GPS的數據更新率是20 Hz,為了作圖清晰直觀,采用提取1 Hz的實測數據進行處理,數據長度為1000 s。圖1～圖6是應用前面所述的方法對實測數據的高度和速度進行多項式擬合并進行誤差分離的結果。

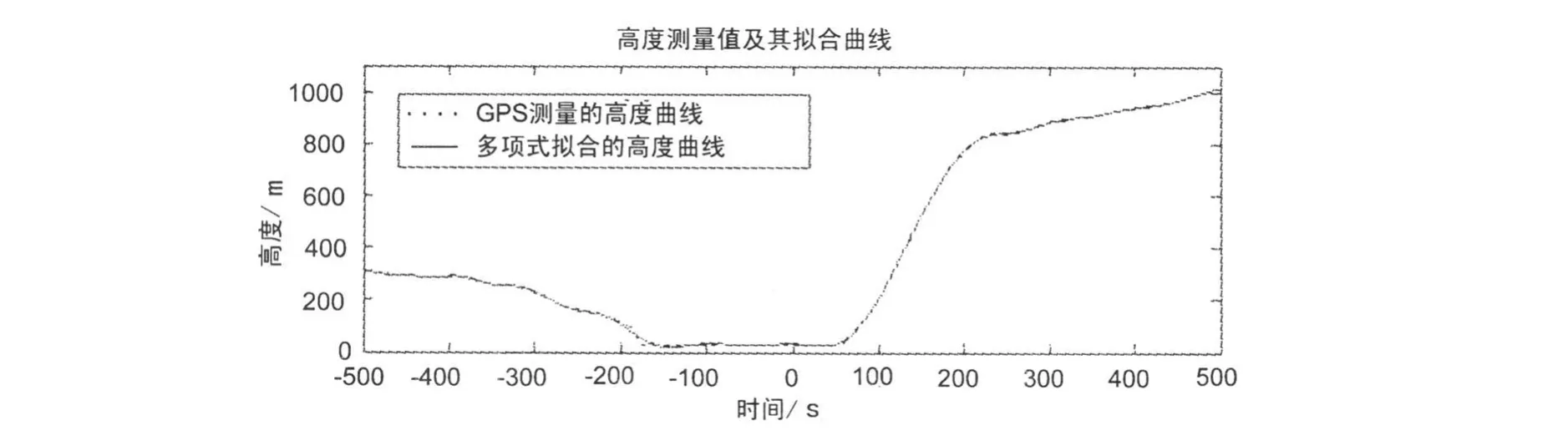
圖1 高度測量值及其擬合曲線

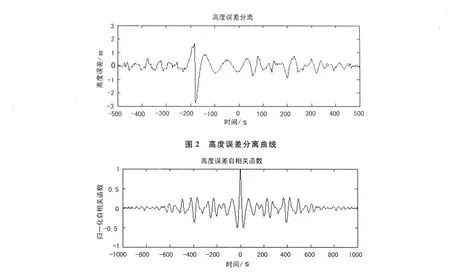
圖3 高度誤差自相關函數

圖1、2、3表示的是GPS高度數據分析結果。從圖1可以看出,多項式能較好擬合無人機飛行高度曲線;圖2、3顯示高度誤差具有明顯的周期性和隨機性,其自相關函數緩慢衰減且周期振蕩。圖4、5、6則表示對與高度記錄相同時段所對應的飛行速度曲線分析結果。從分離出的速度誤差來看,它與高度誤差一樣,具有周期性和隨機性,其自相關函數同樣表現出振蕩衰減性質。圖2、圖5中的出現數據跳變,是因為在此期間無人機處于俯沖階段,姿態變化較大,引起短暫衛星失鎖,使整周模糊度發生跳變所致。對該時段的其他的GPS數據采用上述處理方法,可以得到類似的結論。

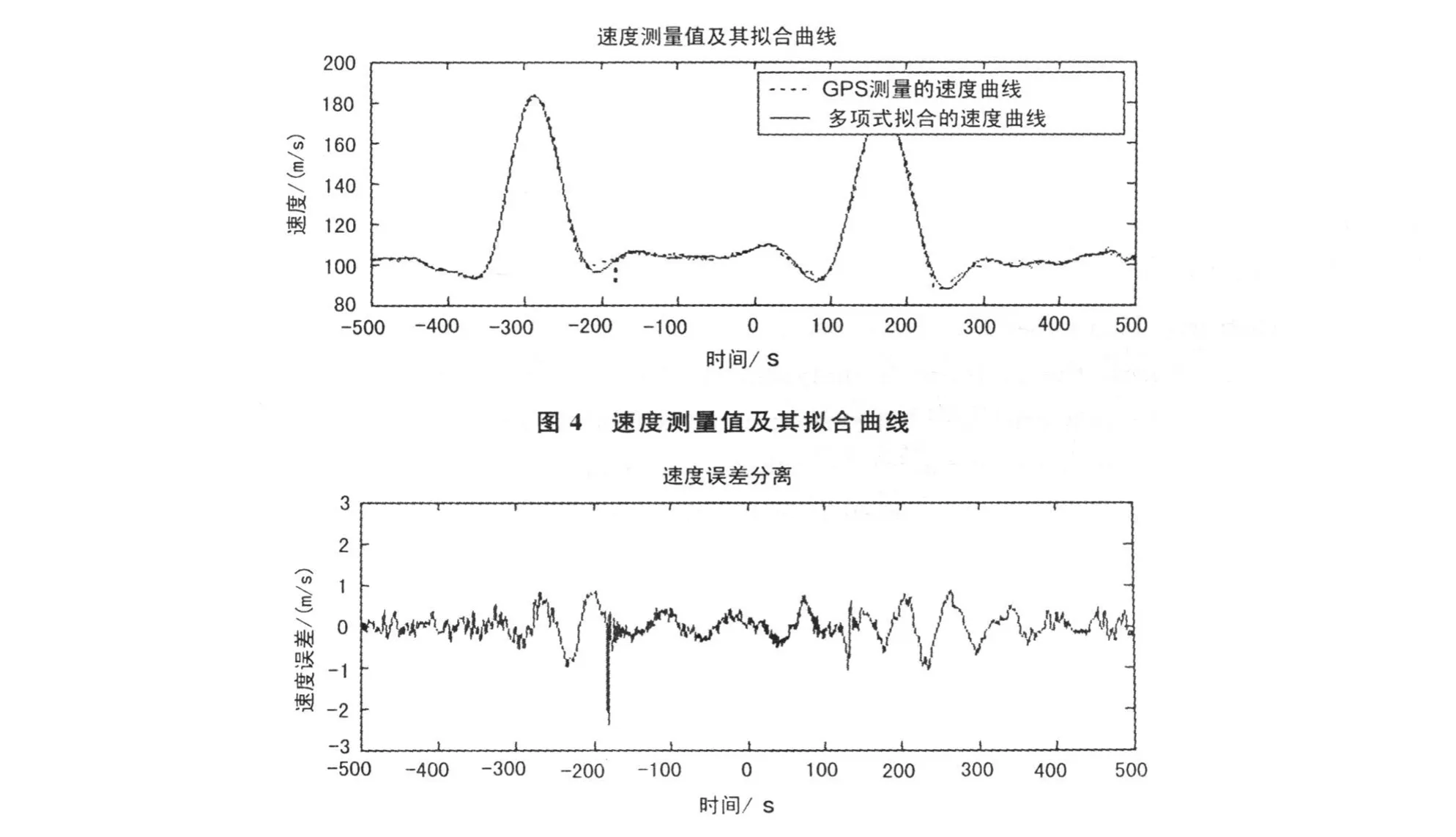
圖5 速度誤差分離曲線

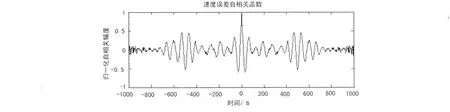
圖6 速度誤差自相關函數

5 結 論

經過理論分析及實例驗證,為GPS動態測量誤差的統計分析確立了完整的分析處理方法。除上述誤差特性、理論基礎、系統誤差分離以外,還包括數據的預處理(數據分析、野點判別及修復等)、多項式和AR模型階數的判別、非線性模型、平穩性檢驗、隨機誤差估計的性質及無偏修正、AR模型建模的遞推算法、非線性建模方法、利用BTB矩陣性質構造多項式(非正交)參數估計的遞推算法等。限于篇幅,這些問題將在后續的研究中再補充討論。

[1] 歐吉坤,王振杰.GPS精密測量中系統誤差的分離方法[J].數據采集與處理,2003,12(4):365-368

[2] 李洪濤,許國昌,薛鴻印,等.GPS應用程序設計[M].北京:科學出版社,1999:256-262

[3] 費業泰.誤差理論與數據處理.第5版[M].北京:機械工業出版社,2005:162-174.

[4] 梁晉文,陳林才,何 貢,等.誤差理論與數據處理.第2版[M].北京:中國計量出版社,2001:136-162.