基于EM算法的OFDM系統頻偏跟蹤和信號檢測技術*

任雪峰 蔣宇中 劉 旋

(海軍工程大學通信工程系 武漢 430033)

1 引言

OFDM[1]是一種具有高效頻譜利用率信號傳輸方案。OFDM系統具有抗多徑能力強,實現簡單,帶寬擴展性強,易于與空時編碼多天線技術相結合等優點。因此它被的應用于軍事通信[2]、數字地面廣播[3]、無線局域網[4]等領域,并成為下一代移動通信(4G)的核心技術之一[5]。但是OFDM系統對載波頻偏具有高度的敏感性[6],這嚴重地影響了整個系統的性能,這就要求對系統的頻偏進行準確的估計。

本文的背景為OFDM系統在短波通信中的應用,考慮到短波信道中多普勒頻移最大可以達到6Hz,而且多普勒頻移是一個時變量,因此載波的頻偏也是時變的。而傳統的頻偏估計算法一般是在AWGN信道中設計的,把頻偏看成是一個不變的量,利用導頻或者是特殊的前導符號對頻偏進行估計[7～9],假如信道頻偏是時變的則這類的方法是不合適的。即使初始頻偏估計的很精確,但是下一幀信號頻偏產生了漂移那么原來的估計也是不準確的,因此這類算法不能用于時變頻偏的跟蹤。本文基于這一問題,根據最大似然檢測準則,提出了一種基于EM算法的時變頻偏跟蹤和信號檢測技術。本算法不但可以跟蹤出時變的頻偏,而且可以達到一個最大似然檢測的目的。計算機仿真證明本文算法要比利用循環前綴的頻偏跟蹤算法[10]更準確,而且可以接近頻偏已知時的誤碼率性能。

2 帶載波頻偏的OFDM系統模型

下面考慮信號通過一個存在頻偏的AWGN信道傳輸的OFDM 系統,系統 FFT變換點數為M,現在忽略信道的沖擊響應,只考慮頻偏對系統的影響,則接收信號的時域表示為:

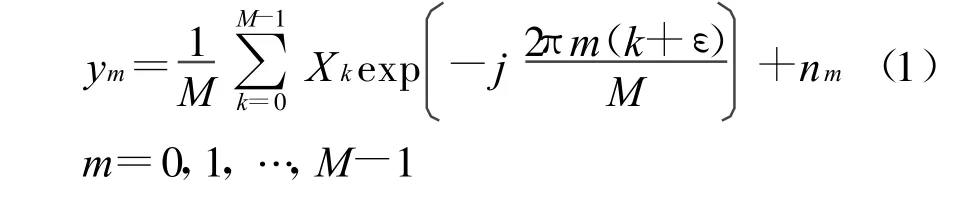
其中,ε是信道的相對頻偏(實際頻偏與載波間間隔的比值)。假設絕對頻偏為 Δf,系統的采樣率為Fs則ε=Δf/(Fs/M)。一般假設整數倍頻偏已經被準確的估計出來了,頻偏小于子載波間隔的一半,即|ε|＜0.5。為后面的處理方便,可將式(1)變換寫成矩陣形式,其中參數設置如下:

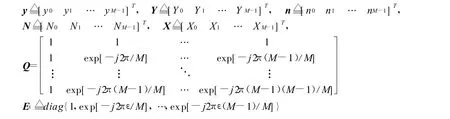
其中,Q是FFT變換矩陣,(1/M)QH是FFT反變換矩陣,即QQH/M=QHQ/M=IM,N=Qn,Eε為頻偏引入量。因此對式(1)進行FFT變換,可以寫為:

3 EM頻偏跟蹤與信號檢測算法

3.1 EM算法引入

這里僅僅考慮頻偏對系統性能的影響,所以信號的最大似然檢測問題可以寫為:

由式(3)可以看出,若直接計算ML判決則會涉及到未知隨機變量ε的多重積分,因此復雜度難以接受。由于EM算法是實現極大似然估計的一種有效方法,它能通過假設隱變量的存在,極大地簡化似然方程[11]。因此本文選擇使用EM算法對時變頻偏進行跟蹤和信號檢測。EM算法表達如下:

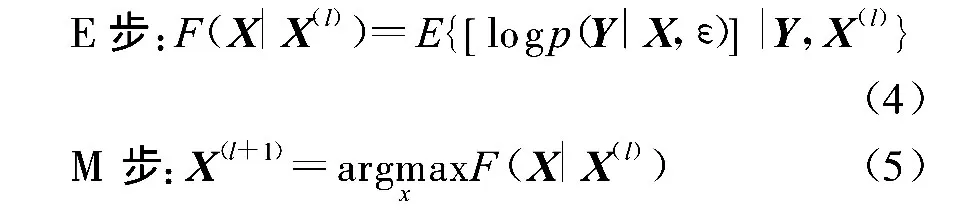
這里,X(l)為第l次EM迭代數據符號的硬判決,顯然對數似然函數logp(Y|X(k))作為l的函數是非下降的[11],并且在通常條件下,EM算法收斂于一個局部的穩定點。

3.2 EM算法的求解過程

在E步中,數據期望是相對于在已知Y和X(l)條件下的載波頻偏ε的求取。ε的條件后驗分布可表示為:

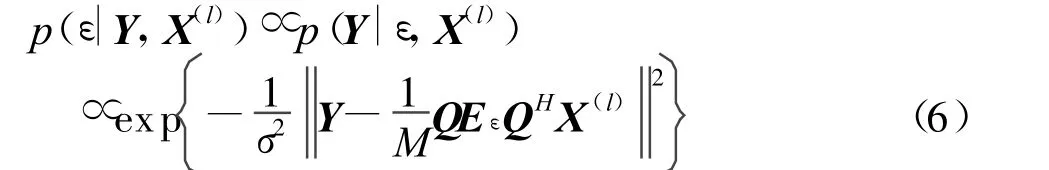
由于在式(2)中ε的非線性模型,因此式(6)中ε的條件后驗分布不是通常使用的分布。因此無法直從分布函數中抽取樣本,因此我們選用局部線性化的Gibbs取樣[12]。具體步驟如下:首先對式(2)兩邊做IDFT反變換得:

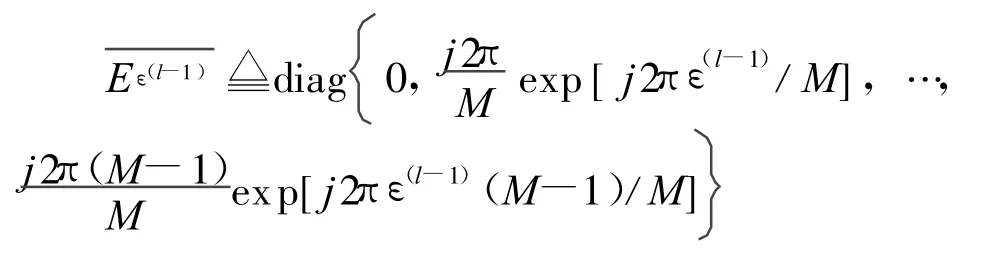
基于局部線性化信號模型,ε的條件后驗分布為高斯分布,即 p(ε|Y,X(l))～N(με,σ2ε)其中:

3.3 算法實現框圖和步驟

本算法的實現框圖如圖1所示。

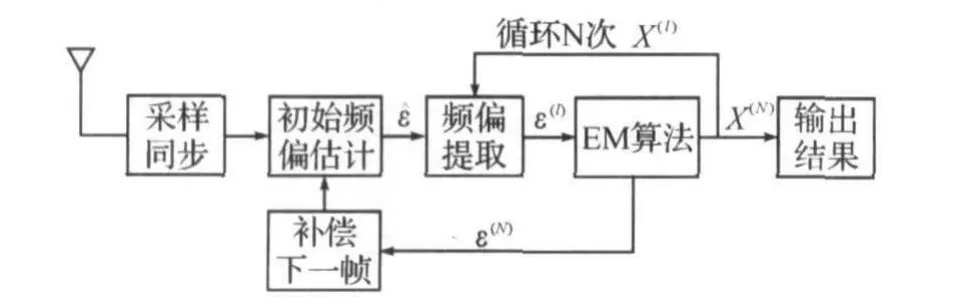
圖1 EM算法框圖

1)首先利用文獻[9]中的頻偏估計算法,利用重復前導符號估計出初始頻偏^ε,利用最大似然算法計算出X(0);

5)將ε(N)補償到下一幀的頻偏中,再重復1),2),3),4)。

4 仿真結果分析

4.1 仿真參數設定

計算機仿真將每一幀的OFDM信號都加上了一個以頻偏為8Hz為中心的隨機的頻偏,這樣更能檢驗算法的跟蹤性能。通過以上的僅帶頻偏OFDM模型的設計,以及基于EM算法的頻偏跟蹤和信號檢測算法的推導,本系統的仿真參數設定如表1所示。

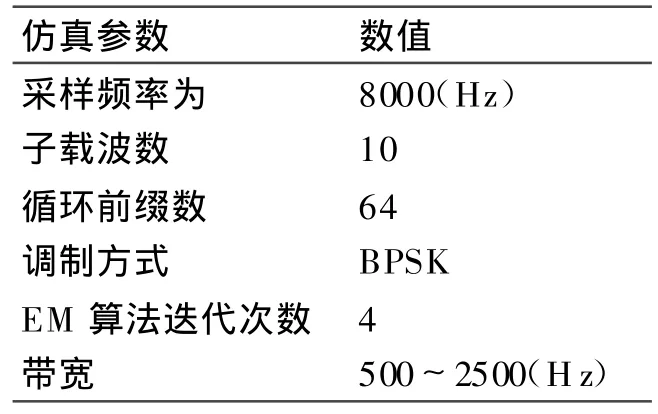
表1 仿真參數

4.2 仿真結果

圖2為EM算法跟蹤到的頻偏與仿真所加的原始頻偏的對比,截取了20幀的OFDM 信號,由圖可以看出三次迭代的頻偏變化軌跡基本與所加頻偏變化軌跡一致,這說明算法可以實現時變頻偏的跟蹤。

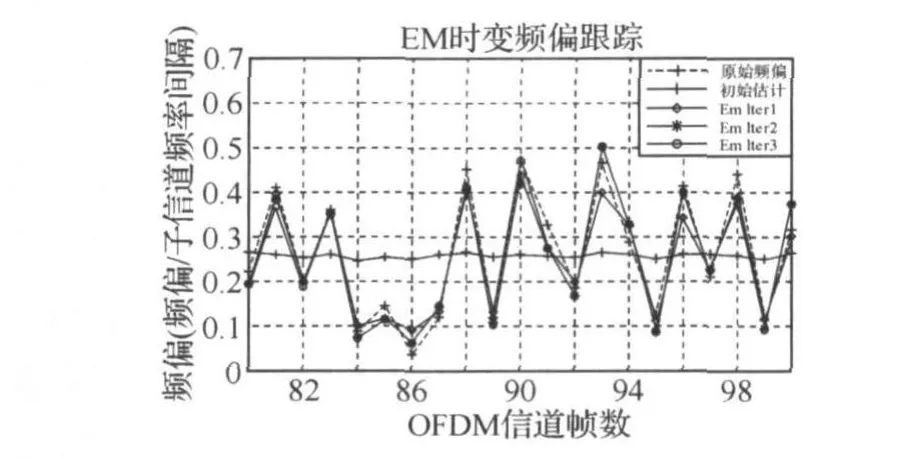
圖2 EM算法頻偏跟蹤

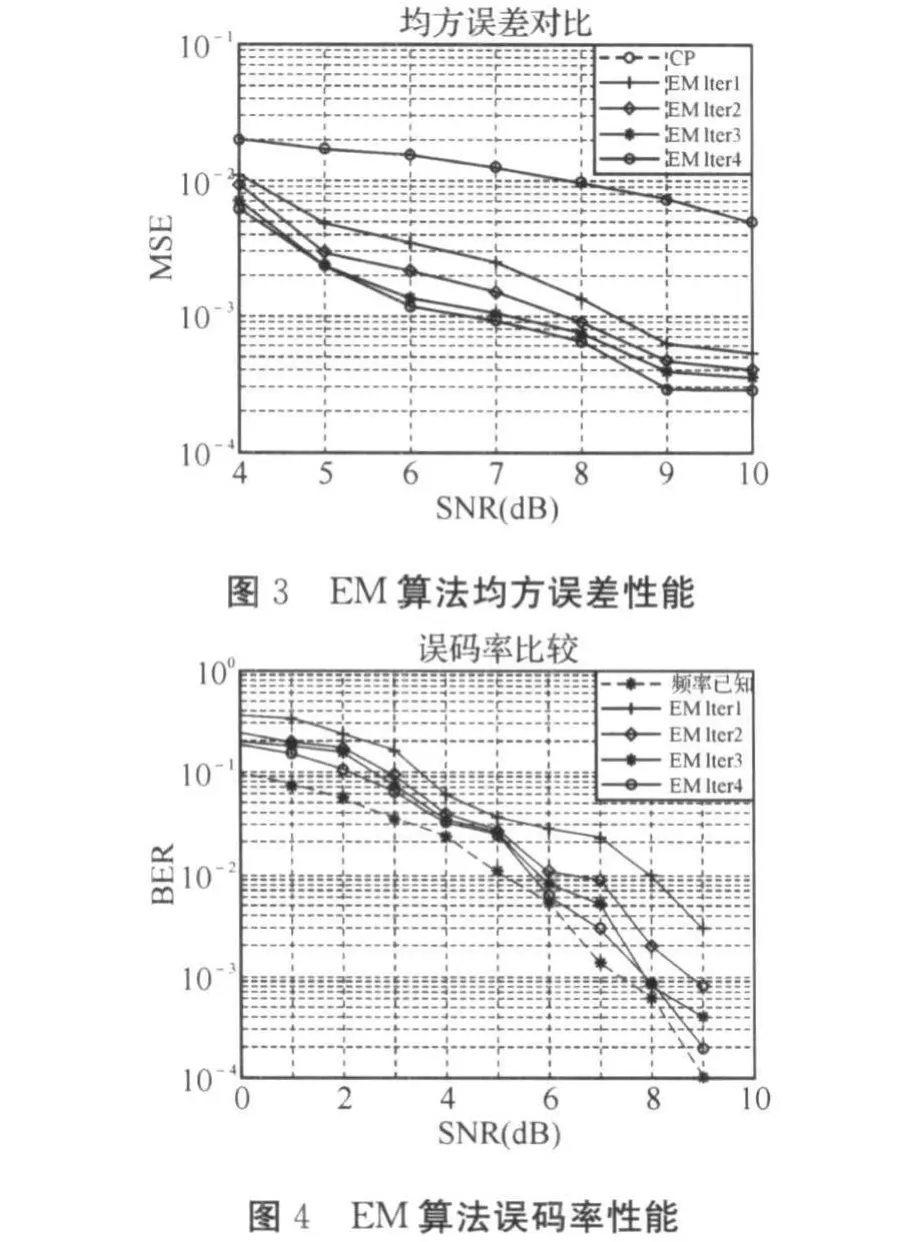
圖3給出了EM算法頻偏跟蹤與利用循環前綴進行頻偏跟蹤[10]的均方誤差(MSE)比較。由圖可知基于EM算法的頻偏跟蹤算法的跟蹤精度要優于利用循環前綴進行頻偏跟蹤算法。隨著EM算法迭代次數的增加跟蹤的精度也隨之增加,這樣就能有效的跟蹤時變的頻偏。試驗設計中頻偏波動較大可以有效跟蹤頻偏,在實際的通信系統頻偏波動不大的情況下更能準確的跟蹤頻偏。由圖3還可以看出算法的收斂速度比較快,基本上經過3次迭代就基本收斂了。

圖4給出了隨機頻偏條件下EM算法信號檢測的誤碼率與頻偏已知時的誤碼率比較。由圖可知隨著迭代次數的增加,EM算法的誤碼率性能可以接近頻偏已知時的誤碼率性能。這也從一個側面說明了EM算法可以有效的跟蹤通信系統的時變頻偏。其原因為EM算法是根據ML檢測準則推導得出的,因此可以達到最佳檢測的目的。

5 結語

本文考慮到實際信道下OFDM系統的頻偏是一個時變量,因此除了利用導頻對頻偏進行估計外,還必須對頻偏進行實時的跟蹤。本論文根據這個思想提出了基于EM算法的頻偏跟蹤和信號檢測技術。本算法以ML檢測為依據,使頻偏跟蹤值能夠滿足最佳檢測的條件,因此得出的跟蹤值是最有效的。經過仿真分析得知這種方法可以得到比較準確的頻偏跟蹤效果,從而改善由于頻偏的漂移而引起的系統性能下降。算法的不足之處在于算法較復雜,實現要求比較高,因此怎樣簡化算法,從而在真正OFDM系統中實現算法將是下一步的研究重點。

[1]Chang R.W,Gibby R.A.A Theoretical study of performance of an orthogonal multiplexing data transmission scheme[J].IEEE Transaction on Communications,1968,16(4):529～540

[2]R.W.Chang.Synthesis of band-limited orthogonal signals for multichannel data transmission[J].Bell Syst.Tech.J.Dec,1966:1775～1796

[3]ESTI.Digital video broadcasting framing structure channel coding,and modulation for digital terrestrial television[J].1997(8):300～744

[4]ANSI/IEEE STD 802.11,Part 11:Wireless LAN Medium Access Control(M AC)and PhysicalLayer(PHY)Specification,2003

[5]A.Chuang,N.Sollenberger.Design considerations and initial physical layer performance results for a space time coded OFDM 4G cellular network[J].in Proc.IEEE PIM RC'02,2002,2(9):192～ 196

[6]T.Pollet,M.V.Bladel,M.Moeneclaey.BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise[J].IEEE Transactions on Communication,1995,43(2/3/4):191～193

[7]Timothy M.Schmidl and Donald C.Cox,Robust frequency and timingsynchronization for OFDM[J].IEEE Transactions on Communication,1997,45(12):1613～1621

[8]P.H.Moose.A technique for orthogonal frequency division multiplexing frequency offset correction[J].IEEE Transactions on Communication,1994,42(10):2908～2914

[9]Michele Morelli,Umberrto Mengali.An improved frequency offset estimator for OFDMapplications[J].IEEE Communications Letters,Mar,1999(3):75～77

[10]J.J.van de Beek,M.sandell,P.O.Borjesson.M L estimation of time and frequency offset in OFDM systems[J].IEEE T ransactions on Signal Processing,1997,45(7):1800～1805

[11]G.J.Mclachlan,T.Krishnam.The EM Algorithm and Extension[M].Wiley,New York,1997:126～178

[12]B.Lu,X.Wang.Bayesian blind turbo receiver for coded OFDM systems with frequency offset and frequency-selective fading[J].IEEE J.Select.Areas Comm,2001,19(12):2516～2527