一種基于RSSI的無(wú)線傳感器網(wǎng)絡(luò)的改進(jìn)定位算法*

馮成旭 劉 忠 程遠(yuǎn)國(guó)

(海軍工程大學(xué)電子工程學(xué)院 武漢 430033)

1 引言

在無(wú)線傳感器網(wǎng)絡(luò)的許多應(yīng)用中,監(jiān)測(cè)到事件的位置信息至關(guān)重要,定位技術(shù)是關(guān)鍵的技術(shù)之一。提到定位技術(shù),我們不難想到全球定位系統(tǒng)GPS。但是采用GPS技術(shù)的系統(tǒng),往往用戶節(jié)點(diǎn)能耗高、體積大、成本高,這些特點(diǎn)使得GPS技術(shù)并不適用于低成本自組織的無(wú)線傳感器網(wǎng)絡(luò)。因此,無(wú)線傳感器網(wǎng)絡(luò)定位已經(jīng)成為當(dāng)今一個(gè)很重要的研究方向和熱點(diǎn)問(wèn)題。

在傳感器網(wǎng)絡(luò)中,定位算法通常劃分為基于距離(range-based)的定位算法和與距離無(wú)關(guān)(rangefree)的定位算法[2]。基于距離的定位中,常采用的方法有:基于到達(dá)時(shí)間 TOA的定位、基于到達(dá)時(shí)間差TDOA的定位、基于接受信號(hào)強(qiáng)度指示RSSI的定位和基于到達(dá)角度AOA的定位等。與距離無(wú)關(guān)的定位算法主要有:質(zhì)心算法、DV-Hop算法、Amorphous算法、APIT算法等等[1]。其中最常用的是利用錨節(jié)點(diǎn)到未知節(jié)點(diǎn)的RSSI(接受信號(hào)強(qiáng)度指示)[4]值來(lái)估算未知節(jié)點(diǎn)到錨節(jié)點(diǎn)的距離,從而實(shí)現(xiàn)未知節(jié)點(diǎn)的定位,因?yàn)樗恍枰砑尤魏晤~外的硬件設(shè)備,只是在現(xiàn)有的硬件基礎(chǔ)上讀取信號(hào)的場(chǎng)強(qiáng)值再經(jīng)過(guò)數(shù)據(jù)處理和算法實(shí)現(xiàn)便可定位。

2 算法原理

2.1 三邊測(cè)量法

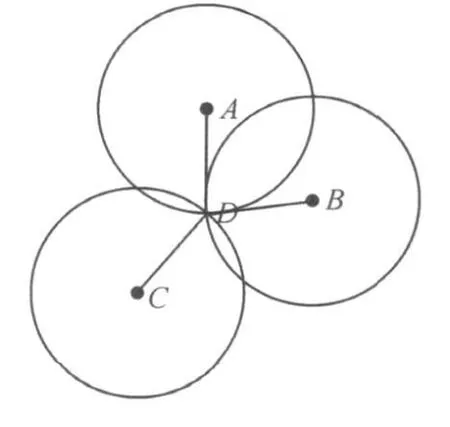
圖1 三邊測(cè)量法

在基于RSSI的定位中,最常見(jiàn)的便是三角形質(zhì)心定位算法[6]和加權(quán)質(zhì)心定位算法[3]。而三角形質(zhì)心定位算法的理論基礎(chǔ)是三邊測(cè)量法[1]。如圖1所示。

如圖 1所示,已知A、B、C三個(gè)節(jié)點(diǎn)的坐標(biāo)分別是(xa,ya)、(xb,yb)、(xc,yc),D點(diǎn)的坐標(biāo)是(x,y),它們到D點(diǎn)的距離分別為da,db,dc,則它們存在下列關(guān)系:

2.2 三角形質(zhì)心定位法

然而,在實(shí)際的基于RSSI距離的定位中,由錨節(jié)點(diǎn)到未知節(jié)點(diǎn)的RSSI值換算出來(lái)的距離值并不是精確的,而且由于電磁場(chǎng)信號(hào)的衰減,換算出來(lái)的這個(gè)距離值要大于從未知節(jié)點(diǎn)到錨節(jié)點(diǎn)的實(shí)際距離。因此,三邊測(cè)量法只是理想狀態(tài)下的模型,然而真實(shí)的模型應(yīng)該是如圖2所示。

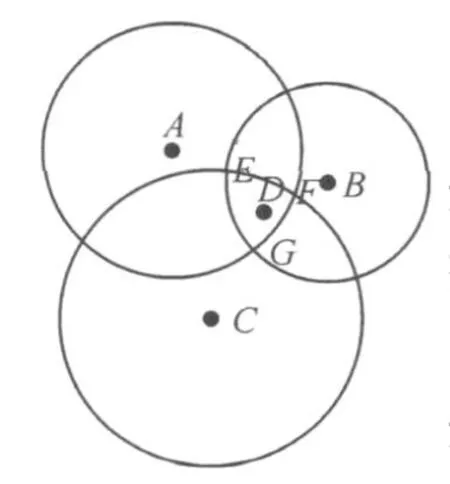
圖2 三角形質(zhì)心定位算法

如圖2所示,D為未知節(jié)點(diǎn),A、B、C為錨節(jié)點(diǎn)。分別以通過(guò) A、B、C 到D 的 RSSI值換算出的距離值為半徑作圓。由于D必定在A、B、C相應(yīng)的通信半徑以內(nèi),因此三圓必定會(huì)有重疊的區(qū)域,如圖中弧EF、弧FG和弧GE所包圍的區(qū)域就是該重疊區(qū)域。而且,未知節(jié)點(diǎn)D的實(shí)際位置必定在該重疊區(qū)域內(nèi)。然后,再對(duì)△EFG求質(zhì)心,未知節(jié)點(diǎn)D的位置就是該質(zhì)心的坐標(biāo)。即D的坐標(biāo)為

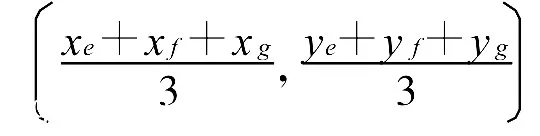
2.3 改進(jìn)的算法分析

但是,三角形質(zhì)心定位算法在實(shí)際環(huán)境測(cè)試中也有諸多不足:

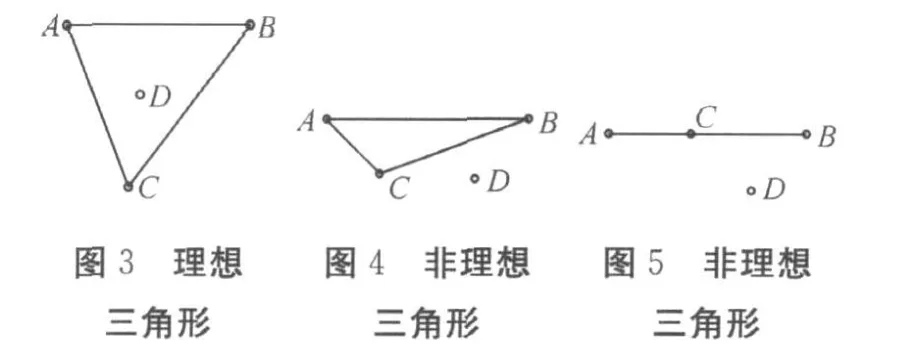
1)三角形質(zhì)心定位算法只適用于理想三角形,即未知節(jié)點(diǎn)的位置在三個(gè)參與定位的錨節(jié)點(diǎn)所構(gòu)成的三角形的內(nèi)部如圖3。在實(shí)際的環(huán)境中,因?yàn)殄^節(jié)點(diǎn)是大規(guī)模隨機(jī)布放的,因此必定存在一些非理想的三角形的情形并不適用于三角形質(zhì)心定位算法,如圖 4未知節(jié)點(diǎn)并不在錨節(jié)點(diǎn)三角形ABC的內(nèi)部;如圖5,與未知節(jié)點(diǎn)相鄰的3個(gè)錨節(jié)點(diǎn)并不能構(gòu)成三角形。在這些非理想三角形的情形下,三角形質(zhì)心定位算法并不適用,如果不予考慮的話必定帶來(lái)更嚴(yán)重的誤差。所以,考慮將該算法進(jìn)行優(yōu)化,在進(jìn)行三角形質(zhì)心定位算法之前進(jìn)行理想三角形驗(yàn)證。驗(yàn)證未知節(jié)點(diǎn)D是否在由三個(gè)錨節(jié)點(diǎn)所構(gòu)成的三角形內(nèi)部,如果不在其內(nèi)部則將該三角形進(jìn)行舍棄,繼續(xù)尋找,直到找到理想的三角形后再進(jìn)行三角形質(zhì)心定位算法。

2)三角形質(zhì)心定位算法只是采用了3個(gè)錨節(jié)點(diǎn)的RSSI數(shù)據(jù)進(jìn)行定位,并未利用整個(gè)網(wǎng)絡(luò)的數(shù)據(jù),從而造成了有效資源的浪費(fèi)。而且,當(dāng)這錨節(jié)點(diǎn)因偶然因素造成數(shù)據(jù)失真時(shí),會(huì)給定位帶來(lái)更大的誤差。因此,考慮將網(wǎng)絡(luò)中更多的理想三角形參與定位,從而給未知節(jié)點(diǎn)一個(gè)更準(zhǔn)確的定位。

3)三角形質(zhì)心定位算法并沒(méi)有考慮RSSI數(shù)值對(duì)距離的影響程度。在實(shí)際的無(wú)線電傳播路徑損耗模型中,RSSI值的衰減與距離的增加并不是線性關(guān)系。隨著未知節(jié)點(diǎn)到錨節(jié)點(diǎn)距離的增加,由RSSI數(shù)值的偏差產(chǎn)生的換算距離的誤差會(huì)迅速增大。因此,考慮在進(jìn)行定位算法時(shí)引入權(quán)重系數(shù)來(lái)體現(xiàn)錨節(jié)點(diǎn)對(duì)未知節(jié)點(diǎn)位置的影響程度,從而來(lái)減小誤差。其基本思想是:RSSI數(shù)值越大的錨節(jié)點(diǎn),對(duì)未知節(jié)點(diǎn)位置的影響力越大。在進(jìn)行質(zhì)心定位算法時(shí),將每一個(gè)決定質(zhì)心的點(diǎn)的坐標(biāo)都乘以一個(gè)權(quán)重系數(shù),以此來(lái)綜合權(quán)衡計(jì)算得出最終的未知節(jié)點(diǎn)位置。

2.4 改進(jìn)的算法原理

針對(duì)第一個(gè)問(wèn)題,理想三角形優(yōu)選的解決方案,最佳莫過(guò)于近似三角形內(nèi)點(diǎn)測(cè)試法APIT[4]中的核心思想。APIT測(cè)試的基本原理如圖6、圖7所示。

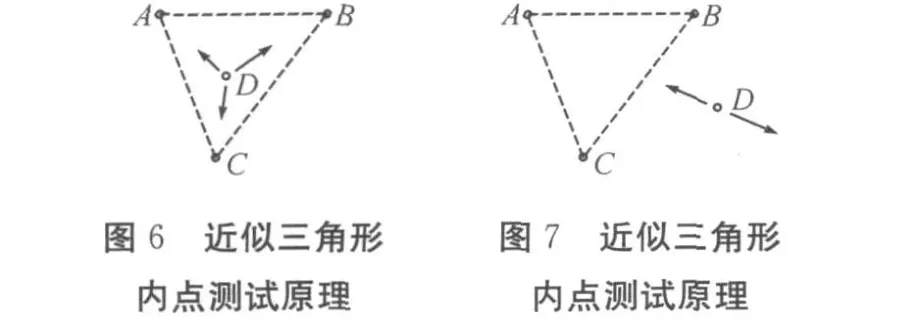
假設(shè)存在一個(gè)方向,節(jié)點(diǎn)D沿著這個(gè)方向移動(dòng)時(shí)會(huì)同時(shí)接近或者遠(yuǎn)離A、B、C三個(gè)節(jié)點(diǎn),那么節(jié)點(diǎn)D位于△ABC之外,如圖7;否則節(jié)點(diǎn)D位于△ABC之內(nèi),如圖6。

而在實(shí)際的環(huán)境測(cè)試中,如果未知節(jié)點(diǎn)D收到的RSSI數(shù)值在增大,則說(shuō)明D在遠(yuǎn)離錨節(jié)點(diǎn);反之,如果D收到的RSSI數(shù)值在減小,則說(shuō)明D在接近錨節(jié)點(diǎn)。

利用APIT算法的核心思想來(lái)進(jìn)行理想三角形的優(yōu)化選擇,可以看到如上圖中的兩種非理想三角形在APIT測(cè)試中會(huì)得出未知節(jié)點(diǎn)D在△ABC之外,對(duì)這種三角形予以舍棄,只保留未知節(jié)點(diǎn)在其內(nèi)部的理想三角形。

對(duì)于第二個(gè)問(wèn)題,改進(jìn)后的算法采用了更多的錨節(jié)點(diǎn)的有效數(shù)據(jù)。對(duì)RSSI數(shù)值達(dá)到一定門限的錨節(jié)點(diǎn)都認(rèn)為是可以參與定位算法的有效節(jié)點(diǎn)。而RSSI數(shù)值低于這個(gè)門限的錨節(jié)點(diǎn)因?yàn)闀?huì)帶來(lái)比較大的誤差所以就予以舍棄。

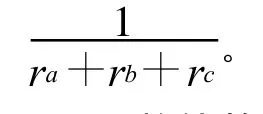
3 算法過(guò)程

定位算法的整體流程:

1)收集所有錨節(jié)點(diǎn)到未知節(jié)點(diǎn)的RSSI數(shù)值,并多次采集取其均值。然后,設(shè)定一個(gè)RSSI值門限,將RSSI數(shù)值低于這個(gè)門限的錨節(jié)點(diǎn)予以舍棄,高于這個(gè)門限的錨節(jié)點(diǎn)視為有效節(jié)點(diǎn),將其數(shù)據(jù)保留。

2)將所有有效節(jié)點(diǎn)按照 RSSI數(shù)值的大小進(jìn)行降序排序,假設(shè)有n個(gè)有效的錨節(jié)點(diǎn)即(R1,R2,R3,…,Rn),這里R1為最大的 RSSI值,Rn為最小的RSSI值。

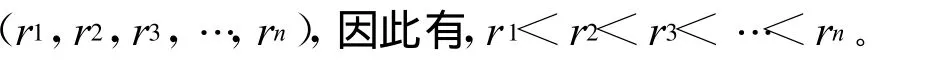
4)將所有的有效錨節(jié)點(diǎn)所組成的三角形集,進(jìn)行理想三角形的優(yōu)化選擇。因此,共有個(gè)三角形,進(jìn)行次近似三角形內(nèi)點(diǎn)測(cè)試后,將測(cè)試結(jié)果為理想的三角形予以保留,非理想的三角形予以舍棄。

5)將保留的理想三角形進(jìn)行如圖2所示的質(zhì)心定位算法,得出未知節(jié)點(diǎn)第一階段定位的近似位置(xi,yi),共有m組近似位置。

7)將所有的理想三角形的輸出結(jié)果(即未知節(jié)點(diǎn)第一階段定位的近似位置(xi,yi))分別與其相應(yīng)的權(quán)重系數(shù)相乘,進(jìn)行加權(quán)質(zhì)心定位。最后的輸出結(jié)果就是未知節(jié)點(diǎn)的坐標(biāo)(X,Y),即

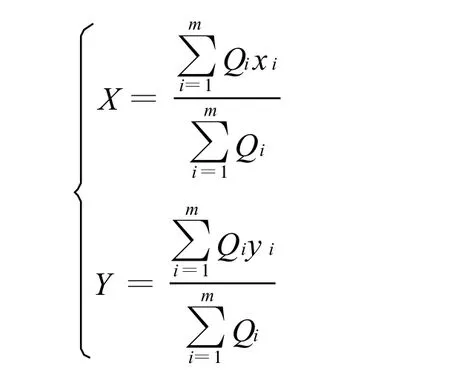
4 算法仿真

在Matlab平臺(tái)上進(jìn)行該改進(jìn)的定位算法仿真。組建一個(gè)虛擬的實(shí)驗(yàn)場(chǎng)景,初始條件為無(wú)線傳感器網(wǎng)絡(luò)在一個(gè)100m*100m的正方形區(qū)域內(nèi)。在此,錨節(jié)點(diǎn)是隨機(jī)的分布在這個(gè)正方形的區(qū)域內(nèi)的。節(jié)點(diǎn)的有效通信半徑設(shè)定為50m。每次仿真結(jié)果都是通過(guò)運(yùn)行算法100次,然后取平均值得到的。

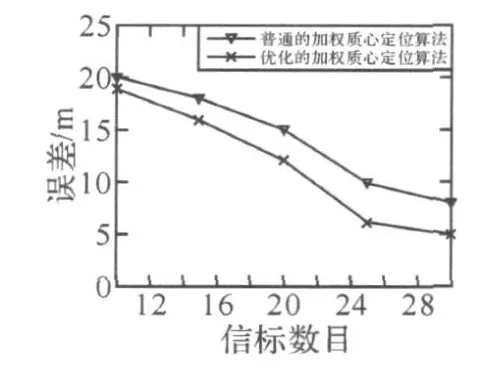
圖8 仿真結(jié)果分析

由圖 8分析可知,當(dāng)錨節(jié)點(diǎn)數(shù)目較少(10個(gè))的時(shí)候,改進(jìn)的算法對(duì)于普通的質(zhì)心定位算法誤差并沒(méi)有明顯的提升。但是隨著錨節(jié)點(diǎn)數(shù)目的增加(20個(gè)以上),誤差就明顯減小了。

5 結(jié)語(yǔ)

本文提出了一種基于RSSI的改進(jìn)定位算法。仿真結(jié)果表明,本文算法比傳統(tǒng)的RSSI定位算法有更好的定位精度。將近似三角形內(nèi)點(diǎn)測(cè)試的核心思想引入理想三角形的篩選,加權(quán)算法中權(quán)重系數(shù)模型的選擇,都能夠明顯減小定位誤差。但是同時(shí)也帶來(lái)了算法復(fù)雜度的提高。因此,下一步的工作是研究理想三角形的優(yōu)化選擇機(jī)制,以降低算法的復(fù)雜度。以進(jìn)一步優(yōu)化算法的整體性能,從而得到更好的定位效果。

[1]孫利民,李建中,陳渝,等,無(wú)線傳感器網(wǎng)絡(luò)[M].北京:清華大學(xué)出版社,2005

[2]王福豹,史龍,任豐原.無(wú)線傳感器網(wǎng)絡(luò)中的自定位系統(tǒng)和算法[J].軟件學(xué)報(bào),2005,16(5):1148～1157

[3]陳維克,李文峰,首珩,等.基于 RSSI的無(wú)線傳感器網(wǎng)絡(luò)加權(quán)質(zhì)心定位算法[J].武漢理工大學(xué)學(xué)報(bào)(交通科學(xué)與工程版),2006,30(2)

[4]He T,Huang C,Blum B M,et al.Range-free localization schemes for large scale sensor networks[C]//Proc 9th Annual Int'l Conf on M obile Computing and Networking(M obiCom),San Diego,CA.,2003:81～95

[5]趙昭,陳小惠.無(wú)線傳感器網(wǎng)絡(luò)中基于RSSI的改進(jìn)定位算法[J].傳感技術(shù)學(xué)報(bào),2009(3)

[6]林瑋,陳傳峰.基于RSSI的無(wú)線傳感器網(wǎng)絡(luò)三角形質(zhì)心定位算法[J].現(xiàn)代電子技術(shù),2009(2)

[7]周四清,陳銳標(biāo).無(wú)線傳感器網(wǎng)絡(luò)APIT定位算法及其改進(jìn)[J].計(jì)算機(jī)工程,2009(4)