多肋式梁橋在全過程中應力重分布研究

張 劍，黃劍峰，葉見曙，俞 博

(1.南京航空航天大學結構工程與力學系，南京210016，jianzhang78@126.com;2.云南農業大學水利水電與建筑學院，昆明650201;3.東南大學橋梁工程研究所，南京210096)

多肋式梁在實際工程中有著廣泛的應用，其在荷載作用下的結構響應一直為工程界關心［1－2］.目前，用三維彈性有限元分析多肋式梁的線彈性行為是容易的，已有多種商業有限元軟件能夠完成.但對于多肋式梁的非線性分析而言，特別是對于預應力混凝土多肋式梁結構，由于預應力效應準確模擬的困難以及三維非線性有限元分析程序編制的復雜性，迄今為止這方面的研究成果出現甚少，大部分研究成果集中在單梁的非線性:如文獻［3］考慮了塑性鉸長度，采用具有假定彎矩－曲率關系的梁單元分析了預應力混凝土T梁結構行為;文獻［4］采用分層梁單元對T梁結構行為進行了非線性分析;文獻［5］應用分層殼單元方法進行了Leonhard鋼筋混凝土深梁的非線性全過程分析;文獻［6］采用梁單元模擬T梁的梁肋，采用分層板單元模擬T梁的翼緣板進行了分析;文獻［7］采用帶剛臂的3節點Timoshenko梁單元模擬T梁的梁肋，采用8節點的Mindlin單元模擬T梁的翼緣板.還有用ANSYS中較受青睞的Solid65單元來進行梁、柱等簡單結構的非線性分析［8－10］，但由于Solid65單元的非線性計算穩定性和收斂性較差［11］，難以用于預應力混凝土多肋式梁和箱梁等較為復雜結構的非線性分析，目前也沒有這方面的研究文獻報道.

由于破壞試驗本身的難度較大，其規模和限制影響因素之多是室內試驗所無法比擬的.迄今為止，國內外進行多肋式梁破壞試驗的文獻資料較為少見.借助于僅有寶貴的工程結構破壞試驗數據，尋求可靠的計算理論來研究多肋式梁成為重要途徑［12］.因此，研究多肋式梁非線性行為的計算方法、編制相應的計算程序是具有理論價值和實際工程意義的.本文著重研究預應力鋼筋對組合殼單元剛度矩陣的貢獻和統一的非線性殼單元模式，并研究工程薄壁多肋式梁的破壞全過程分析方法和應力重分布規律.

1 非線性單元模式的研究

1.1 實體退化殼單元

體單元及相應的退化殼元如圖1和圖2所示.圖1中體單元的控制節點18個，退化殼元的控制節點9個，用于描述退化殼元的信息明顯減少［13］.且假設:退化殼元的垂直于中面的法線在變形后仍為直線，且垂直于殼中面的應力分量假設為零.

圖1 體單元描述

預應力混凝土多肋式梁由混凝土、普通鋼筋和預應力鋼筋組成，其材料性能和應力是ζ的不連續函數.而混凝土的屈服、開裂等結構行為需用到沿殼厚方向的積分來表達.分層法簡潔而有效地解決了此問題，將不連續函數的積分問題化為有限項級數求和問題，且能保證工程精度.沿ζ方向的分層模型如圖3所示.

圖2 退化殼單元描述

圖3 殼元分層模型

2.2 組合殼單元

對于彎曲的預應力鋼筋，用層單元等模擬過于近似，本文研究用組合殼元模擬.組合殼元中預應力鋼筋單元起點A和終點B如圖2所示，利用實體退化殼單元位移插值公式［13］，則鋼筋單元的節點位移可用殼元節點位移表示為

式中:n為殼元節點數，hi為節點i處殼元厚度，為節點i的節點坐標系ν與x軸夾角余弦值，其1余類推、分別為形函數Ni在節點A和節點B的值;ζA、ζB分別為預應力筋起點A和終點B的ζ向局部坐標，δi為殼元的節點位移列陣，Ri為轉換矩陣.并記，則式(1)可寫為:δS=RδC.

則應用虛功原理［14］，推得預應力鋼筋單元對組合殼元剛度矩陣的貢獻:

式中:KP為預應力鋼筋對組合殼元剛度矩陣的貢獻;KS為整體坐標系下預應力鋼筋單元剛度矩陣.

混凝土和普通鋼筋采用分層殼單元模擬，預應力鋼筋采用組合殼單元模擬，則統一的非線性殼單元剛度矩陣推導為

式中:l、m分別為非線性殼單元中混凝土和普通鋼筋的層數，Ke為非線性殼單元剛度矩陣，KjC為殼元中第j層混凝土層的剛度矩陣為殼元中第k層普通鋼筋層的剛度矩陣和均可利用高斯求積公式計算.KP為式(3)的預應力鋼筋對非線性殼元剛度矩陣的貢獻.

2 非線性力學性能描述

2.1 混凝土屈服準則

由于殼元需考慮橫向剪切作用，本文選擇Owen雙參數三軸屈服準則，表達式為

式中:I1為應力張量第一不變量;J2為應力偏量第二不變量;σ0為等效應力，取為單軸抗壓強度fc; α、β為材料參數，由式(4)根據單軸抗壓試驗和雙軸等壓試驗標定

2.2 混凝土強化準則

強化準則確定了塑性變形過程中后繼屈服面(加載表面)的運動.它決定了加載面以及累計塑性應變之間的關系.利用有效應力和有效塑性應變的物理意義，使得混凝土力學行為的描述可用單軸試驗來外推得到多軸時的情況.彈塑性矩陣中的強化參數H'可由有效應力σ對有效塑性應變εp的斜率表示，即

Madrid線型的單軸有效應力σ和有效塑性應變εp關系式為

式中:E0為初始彈性模量;ε0為單軸抗壓強度fc時的總應變，可取為為彈性應變，即為

式中:強化參數H'即可由式(6)和式(8)求出.

2.3 混凝土壓碎準則

混凝土的壓碎斷裂由應變控制，Hinton壓碎準則表達式為

式中:I'1為應變張量第一不變量;J'2為應變偏量第二不變量;εu為混凝土極限壓應變.

2.4 鋼筋材料非線性特性

預應力混凝土多肋式梁的鋼筋材料分為普通鋼筋和預應力鋼筋.普通鋼筋采用殼元中等效厚度的層單元考慮［13］.假定每一鋼筋層的力學性能是單向的，只能承受沿鋼筋方向的軸向力.本文預應力鋼筋采用組合殼單元考慮.采用雙折線強化彈塑性模型模擬鋼筋的本構關系［15］.

單軸有效應力σ和有效塑性應變εp的關系式為

3 非線性分析的收斂準則

在預應力混凝土多肋式梁的非線性分析中，由于考慮了鋼筋混凝土材料非線性效應，涉及到大型非線性有限元方程組的求解問題，本文采用增量－迭代法求解.現有的迭代方法分為:直接迭代法、切線剛度法、割線剛度法和等剛度法等.等剛度法只需一次形成土多T梁分層殼整體剛度矩陣，其后無需重新生成整體剛度矩陣，在一定程度上節省了計算時間，提高了計算效率.本文綜合采用等剛度法和切線剛度法，即在各增量步的第一次迭代時采用切線剛度法，各增量步內的其余迭代計算采用等剛度法.

收斂準則一般分為:力收斂準則和位移收斂準則.在預應力混凝土多T梁橋的非線性分析中，不平衡力常可形成一些平衡力系，使得解不能單調收斂，故本文采用位移收斂準則，取

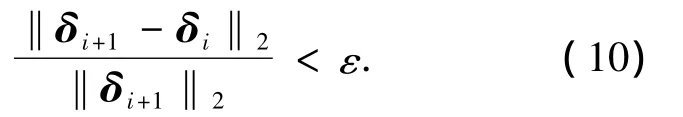
式中:δi為第i增量步的非線性方程組迭代時的收斂解，即預應力混凝土多肋式梁第i增量步整體位移向量;δi+1為第i+1增量步的非線性方程組迭代時的收斂解;ε為收斂容差，取為2.5%.

4 非線性全過程分析

4.1 試驗資料

文獻［12］進行了滬寧高速公路上一預應力混凝土多肋式梁的破壞性試驗研究，這在國內尚屬首次.該多肋式梁橋由6片單梁組成，單梁截面如圖4所示，并沿縱向設有5道橫隔板(2道端橫隔板，3道中橫隔板).單梁長20 m，翼板寬2.08 m，梁高 1.4 m，腹板寬 0.18 m，馬蹄寬0.40 m.橋梁所用材料為50號混凝土和強度級別為1 600 MPa高強鋼絲.橋梁采用在現場整體拼裝式大型鋼模板預制施工，孔道采用金屬波紋管成型，6根預應力鋼束，控制張拉應力1 200 MPa，有效張拉應力1 000 MPa.橋梁支座采用板式橡膠支座，普通鋼筋和預應力鋼筋的詳細布置見文獻［12］.考慮到實橋破壞性試驗加載量巨大，試驗采用鋼材加載方案，以確保試驗順利進行.同時為提高加載效率，文獻［12］采用圖5所示(G1表示第一片單梁肋中心所在位置，其余類推)的偏載加載方式，主梁G1所受均布荷載為主梁G2至主梁G5的2倍，主梁G6近似不受荷載作用，即通過鋼材偏向橋面一側來實現.

圖4 預應力混凝土單T梁的截面圖(m)

圖5 鋼材沿橋面橫向布置

4.2 預應力混凝土多肋式梁的組合殼單元建模

預應力混凝土多肋式梁是典型的工程薄壁結構，采用殼單元模擬是適合的.梁體(主梁和橫隔板)共劃分成715個單元，2 739個節點，其中組合殼單元180個，有限元模型如圖6所示.有限元計算加載方式采用文獻［14］的加載方案，每級每20 m加載49.6 t的均布荷載.橫向加載時，加載點為T梁肋板和頂板的交點處.

4.3 撓度計算結果

應用本文編制的三維非線性有限元程序，在各級荷載作用下，預應力混凝土多肋式梁的偏載端主梁G1的1/4跨、跨中和3/4跨梁底的撓度計算結果與破壞性試驗資料的比較如圖7所示.

從荷載－撓度曲線圖7可知，用非線性有限元程序得到的計算值和試驗值趨勢相同，兩者數據吻合程度良好，這說明了本文采用的實體退化殼單元、鋼筋混凝土材料非線性描述以及預應力鋼筋的組合殼單元模擬等用于預應力混凝土多肋式梁非線性分析的有效性和可靠性.破壞性試驗得到多肋式梁極限承載力約為1 139.37 t，有限元得到多肋式梁極限承載力約為1 240.00 t，相對誤差約為8.82%.

提取各主梁跨中截面梁底的撓度數據，可得相應的荷載－撓度曲線如圖8所示.隨著加載量增加，各主梁截面會出現剛度折減現象.由于加載偏載于主梁G1，在各級荷載作用下，主梁G1撓度最大，撓度發展最迅速，主梁G2至主梁G5撓度依次減小，主梁G6撓度變化不明顯.

4.4 預應力鋼筋應力發展

各主梁1/4跨和跨中截面梁底的預應力鋼筋應力發展規律如圖9，跨中處鋼筋應力的相應數據見表1.

圖6 預應力混凝土多肋式梁有限元模型

圖7 撓度計算結果

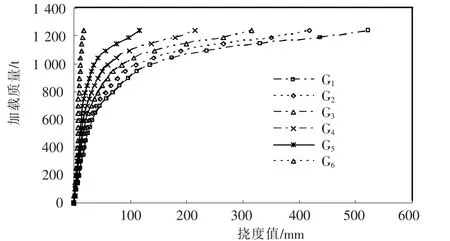
圖8 各主梁跨中荷載－撓度曲線

圖9 各主梁預應力鋼筋應力

由圖9(a)可知，隨著加載量增加，1/4跨截面各主梁的預應力鋼筋應力都有增加，但在整個非線性過程中預應力鋼筋均未發生屈服.由圖9(b)和表1可以看出，隨著加載量增加，跨中截面主梁G6的預應力鋼筋應力變化幅度不大，其余各主梁的預應力鋼筋應力都呈現明顯的增大趨勢.由于偏載作用，主梁G1的預應力鋼筋應力增長速度最快，在加載第19級時，主梁G1的預應力鋼筋首先屈服;繼續加載，主梁G2至主梁G5的預應力鋼筋應力也相繼屈服，直至整個結構破壞.

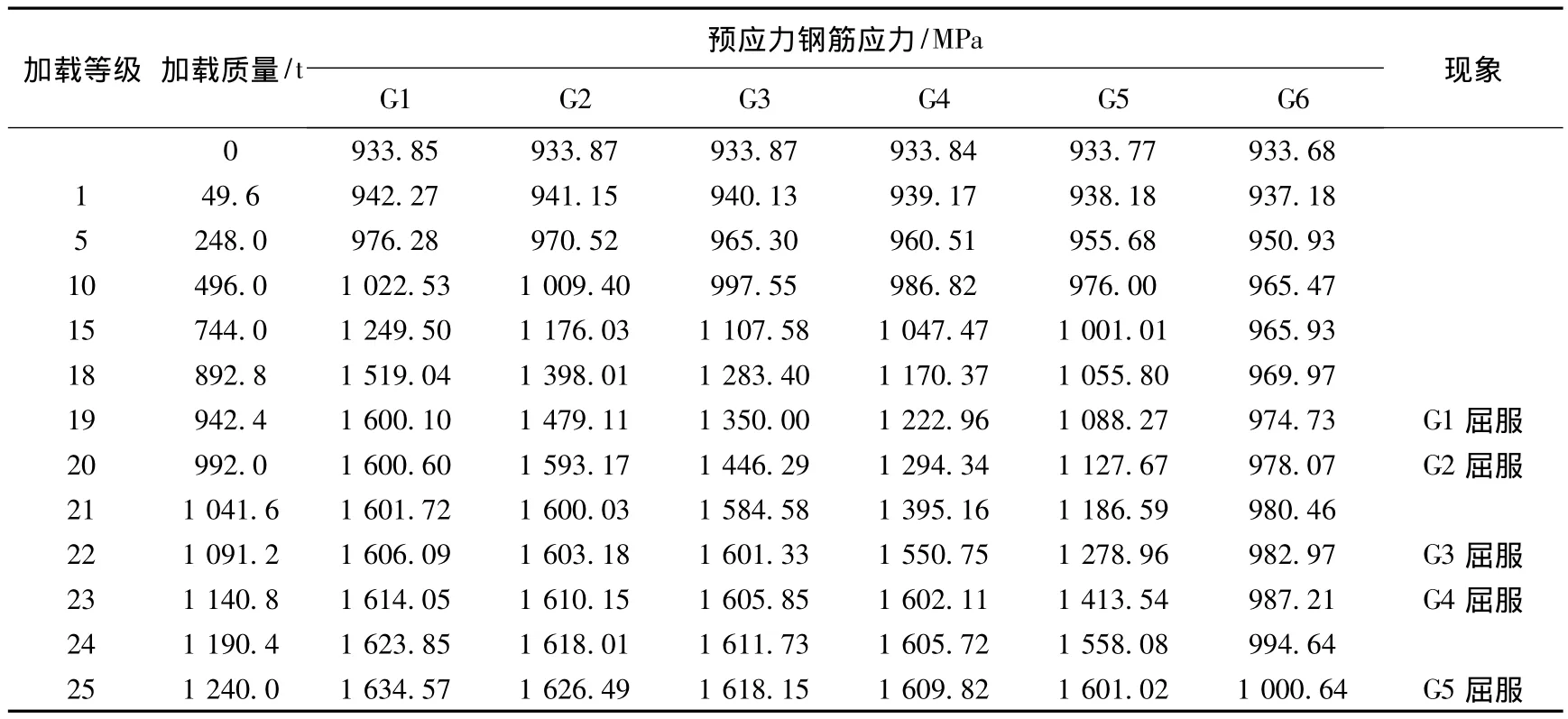
表1 各主梁跨中截面梁底的預應力鋼筋應力

5 結論

1)用實體退化殼單元模擬預應力混凝土多肋式梁是適合的，單元用于非線性分析時表現出良好的數值穩定性和收斂性，計算精度較高.

2)預應力效應的準確模擬是重要的，采用組合殼單元模擬預應力鋼筋及其非線性效應是有效的，這也是對一般用層單元等模擬預應力鋼筋的一種改進.

3)編制預應力混凝土多肋式梁非線性全過程分析程序，計算結果包含大量的有用信息，對典型截面撓度和預應力鋼筋應力發展規律進行了統計分析.該方法也有望在箱梁等結構的非線性分析中得到應用.

［1］SONG H W，YOU D W，BYUN K J，et al.Finite element failure analysis of reinforced concrete T-girder bridges［J］.Engineering Structures，2002，24(2):151－162.

［2］張劍，葉見曙.鋼筋混凝土多T梁結構的分層殼元計算法［J］.水利學報，2006，37(11):1372－1377.

［3］LIN Z D，MICHEL G，A，JOAN R C.Nonlinear flexural behavior of prestressed concrete girder bridges［J］.Journal of Bridge Engineering，2001，6(4):276－284.

［4］FRAGIACOMO M，AMADIO C，MACORINI L.Finiteelement model for collapse and long-term analysis of steel-concrete composite beams［J］.Journal of Structural Engineering，2004，130(3):489－497.

［5］方自虎，孫璨.鋼筋混凝土結構的三維有限元非線性分析［J］.計算力學學報，2006，23(3):377－380.

［6］WENDEL M S，RICHARD E M.Nonlinear FE analysis of steel-concrete composite structures［J］.Journal of Structural Engineering，2000，126(6):662－674.

［7］WONSEOK C，ELISA D S.Nonlinear finite-element analysis of composite steel girder bridges［J］.Journal of Structural Engineering，2005，131(2):304－313.

［8］SANTHAKUMAR R，CHANDRASEKARAN E，DHANARAJ R.Analysis of retrofitted reinforced concrete shear beams using carbon fiber composites［J］.Electronic Journal of Structural Engineering，2004(4):66－74.

［9］梅力彪，周云，陰毅.穿心暗牛腿鋼管混凝土柱單梁節點空間非線性有限元分析［J］.工業建筑，2004，34(9): 81－83.

［10］QUEIROZ F D，VELLASCO P C，NETHERCOT D A.Finite element modelling of composite beams with full and partial shear connection［J］.Journal of Constructional Steel Research，2007，63(4):505－521.

［11］司炳君，孫治國，艾慶華.Solid65單元在混凝土結構有限元分析中的應用［J］.工業建筑，2007，37(1):87－92.

［12］張宇峰.滬寧高速公路擴建工程橋梁極限狀態實橋試驗研究試驗［R］.南京:江蘇省交通科學研究院，2006.

［13］HINTON E，OWEN D R J.Finite element software for plates and shells［M］.Swansea:UK Pineridge Press Ltd，1984.

［14］江見鯨，陸新征，葉列平.混凝土結構有限元分析［M］.北京:清華大學出版社，2005.

［15］呂西林，金國芳，吳曉涵.鋼筋混凝土結構非線性有限元理論與應用［M］.上海:同濟大學出版社，1999.