神經網絡應用于大壩安全評價的方法研究

王玉成

（江蘇省電力設計院，江蘇南京211102）

0 引言

大壩安全評價是一個非常復雜的過程，其過程實際上可以理解為：y=f（x1，x2，……，xn），其中y為大壩安全度，x1，x2，……，xn為影響大壩安全的各種因素，例如變形、裂縫、滲流等。傳統的大壩評價方法往往是富有經驗的專家依據工程實際情況、歷史經驗、物理力學關系等，給出合理恰當的評價，一旦有新情況就需要重新做出判斷。而神經網絡模型可以通過對歷史樣本的自主學習，在輸出的評價結果中再現專家的思維和經驗，得出比較合理的評價結論，節省大量人力物力。

傳統大壩安全評價方法是對變形、滲流、應力分別建立統計模型，然后對監測資料進行回歸分析，不能為神經網絡模型提供合適的學習樣本，因此提出一種新的大壩安全評價方法，為神經網絡應用于大壩安全評價提供可能。

1 大壩安全評價新方法

大壩安全評價是一個極其復雜的過程，各種因素相互影響，錯綜復雜。例如大壩結構安全由變形、滲流、應力等方面決定，而其中變形的安全又由徑、切向水平位移和垂直位移的安全程度決定，徑、切向水平位移的安全程度又由某些重點壩段的徑、切向位移監測值的安全程度決定。因此，可行的方法是逐級而上，對某些重點壩段徑、切向位移監測值的安全度進行評價，得到評價值，然后把它們對大壩整體徑、切向水平位移安全程度的影響值（所占權重）剝離出來，兩者結合考慮得到大壩整體徑、切向水平位移的安全程度值。依此層層而上，最終得到整個大壩的安全程度值。圖1為某大壩安全度評價結構示意圖。

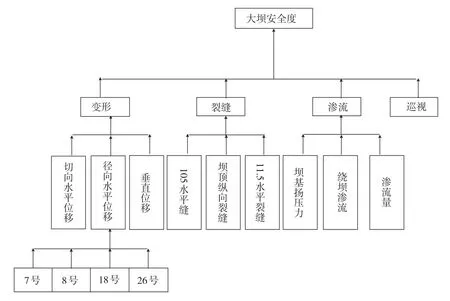
圖1 某大壩安全度評價結構示意圖Fig.1 Schematic drawing of safety evaluation for a dam

采用此種方法理論上可以進行大壩安全度評價，但是需要解決兩個主要問題：如何對評價結構中處于底層位置的重點壩段徑、切向位移觀測值安全度進行評價；如何科學合理剝離出下一級因素對上一級因素安全值的影響程度（權重）。

1.1 安全度值評價

參考有關文獻，將大壩安全指標等級定為5級（正常，基本正常，輕度異常，重度異常，惡性失常），將其用數軸上（0～1）區間內相對應的5段范圍進行量化。

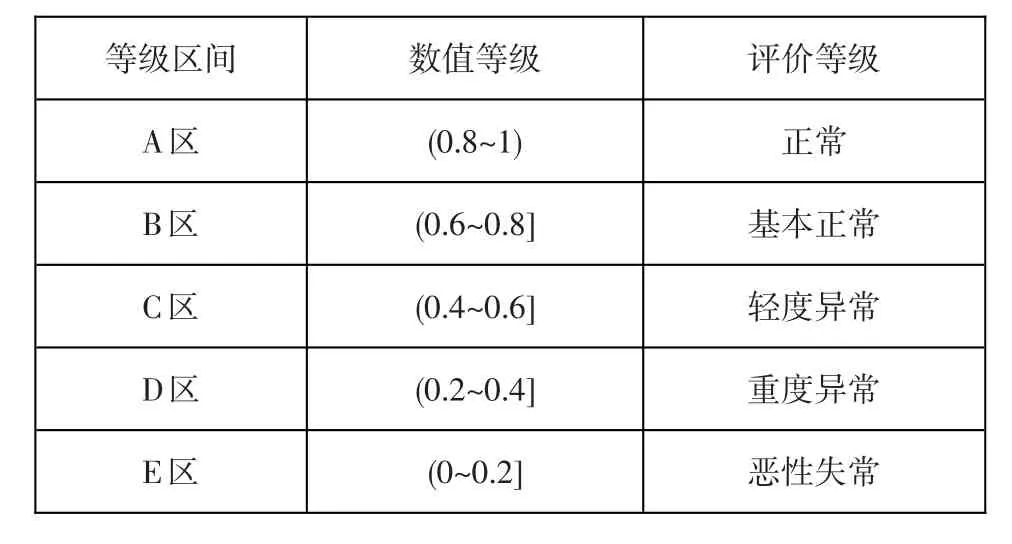
表1 大壩安全指標等級Table 1:Grades of dam safety indexes

大壩原位監測資料在參與大壩安全評價時可以從效應量的數值表現來考慮，主要是將實測值與模型擬合值及所建立的大壩安全監控指標來進行比較。監控指標是用來衡量大壩運行是否正常、安全的一種數值界限。當實測值在監控指標規定的范圍以內或數值以下，一般認為大壩運行是正常的，否則就不安全。大壩安全監控指標可分為警戒值和危險值兩類。警戒值是反映大壩正常與否的界限值，它主要根據觀測量與荷載間的物理關系并結合以往測值的變化范圍和規律來擬定。界限值是反映大壩安全與否的界限值，它主要根據安全要求所限定的效應量數值來確定。

設數學模型表示為：y?=f（x1，x2，……，xn），則監控指標一般可表示為：

式中，[y]為監測量y的監控指標界限；y?為監測量y的統計估計值；xi為影響監測量y的主要環境因素變量；ε為置信帶寬，當采用監控模型法確定監控指標時，可取ε=pS，其中p=1～3，S為模型剩余標準差：

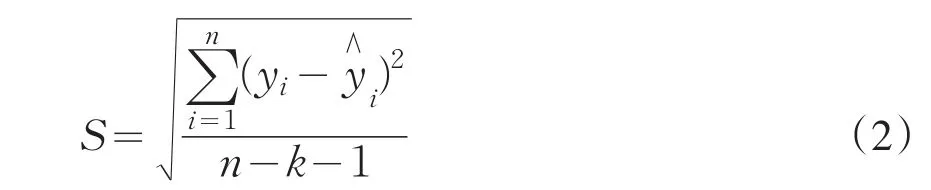
式中n為模型中實測效應量總數，k為實測效應量的自由度。

所以監控指標公式可表示成：

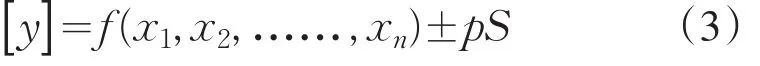
因此評價指標等級區間A區、B區、C區、D區、E區也可以用監控指標來劃定，這樣能使人為劃定的等級區間和通過統計模型回歸分析所得的監控指標相掛鉤，使評價結果更合理，更具科學性。

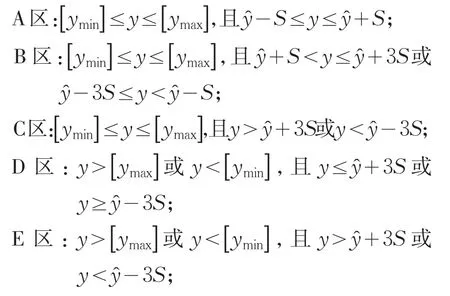
ymax,ymin為監控指標的限制值。

推導可得安全度值計算公式見表2。

表2 安全度值計算公式Table 2:Formulas for dam safety calculation

這樣，評價指標等級區間A區、B區、C區、D區、E區和監控指標相聯系，使人為劃定的等級區間和通過統計模型回歸分析所得的監控指標相掛鉤，解決了大壩安全評價結構最底層因子的安全度評價問題。

1.2 權值分析

在得到大壩安全評價結構最底層因子的安全度評價度值后，如果能確定底層因子相對于上一層因子安全度所占的權重，就能確定上層因子的安全度。本文提出用主成分分析法和層次分析法相結合的方法來確定下層因子的權重。

1.2.1 主成分分析法（PCA）

根據主成分理論，主成分分析直接依據原始實測資料的信息，通過正交變換，把多個相關指標轉化為少量不相關評價指標，并定量描述交互指標在整體系統中貢獻，并通過貢獻量大小來識別對應的各個評價指標的權重值。

PCA的主要步驟是依據大壩監測資料建立監測資料相關矩陣，然后進行一系列的矩陣變換運算，最后得到權重矩陣（過程略）。

1.2.2 層次分析法（AHP）

層次分析法（Analytic Hierarchy Process，AHP）是系統工程中對非定量事件作定量分析的一種簡便方法，它能實現大壩專家主觀判斷的客觀描述。其主要步驟如下：

（1）確定評價目標A和評價因素集U。

（2）構造判斷矩陣P。以A表示目標，ui表示評價因素，ui∈U(1，2，…，n)，uij表示ui對uj的相對重要性數值（也稱為“標度”）(j=1，2，…，n)，則

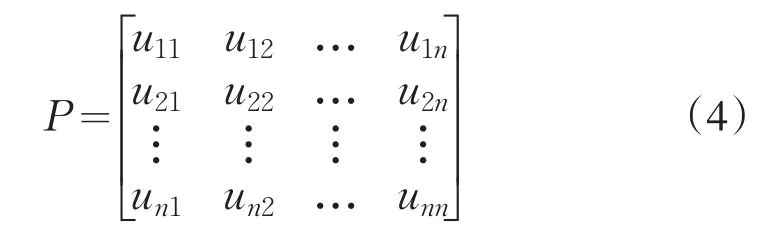
P也稱為A-U判斷矩陣。

（3）權數分配。由A-U矩陣求出最大特征值所對應的單位特征向量。所求單位特征向量各分量即為各評價因素重要性排序，也即權數分配。

（4）檢驗。以上得到的單位特征向量即為所求權向量，為了檢驗權重的分配是否合理，需要對判斷矩陣進行一致性檢驗，使用公式：

式中：CR——判斷矩陣的隨機一致性比率；

CI——判斷矩陣的一般一致性指標，由公式CI=(λmax-n)/(n-1)計算；

RI——判斷矩陣的平均隨機一致性指標，對于1～9階判斷矩陣，RI的值列于表3。

表3 RI值表Table 3:RI values

當CR＜0.1時，即認為判斷矩陣具有滿意的一致性，說明權重系數分配合理，否則就需要調整判斷矩陣，直到取得滿意的一致性為止。

2 實例計算

為了驗證本文提出方法的可行性，采用某大壩1999～2006年間的變形數據進行計算。

該大壩變形因子下屬有徑向水平位移因子、切向水平位移因子、垂直位移因子。根據該大壩本身壩體結構，參考專家意見，選擇底層因子見表4。

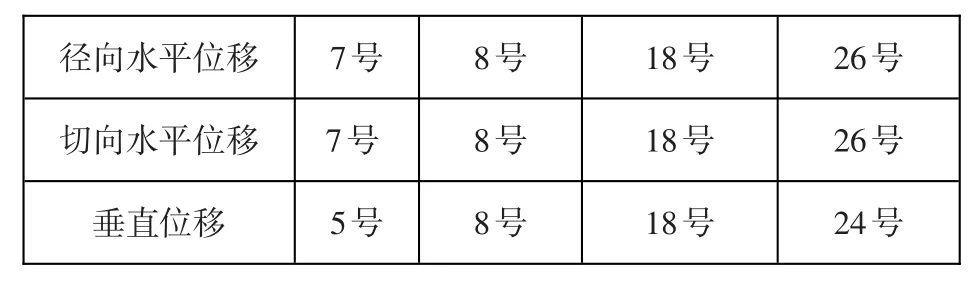
表4 底層因子選擇Table 4:Underlying factors selected

采用1999～2004年的數據進行建模分析，選取2005年1月17日、2月20日、2006年1月6日、2月4日當日的變形安全度值作為檢驗數據（篇幅原因，只選取少量進行說明）。

依照前文所述，先對底層因子進行建模分析，確定監控模型，然后進行安全度判斷，再進行求權工作，層層而上，最后得到位于頂層的大壩整體變形安全度。

現僅將部分中間計算結果列出。

根據所建監控模型及大壩原位觀測數據，根據表2計算得底層因子安全度值。

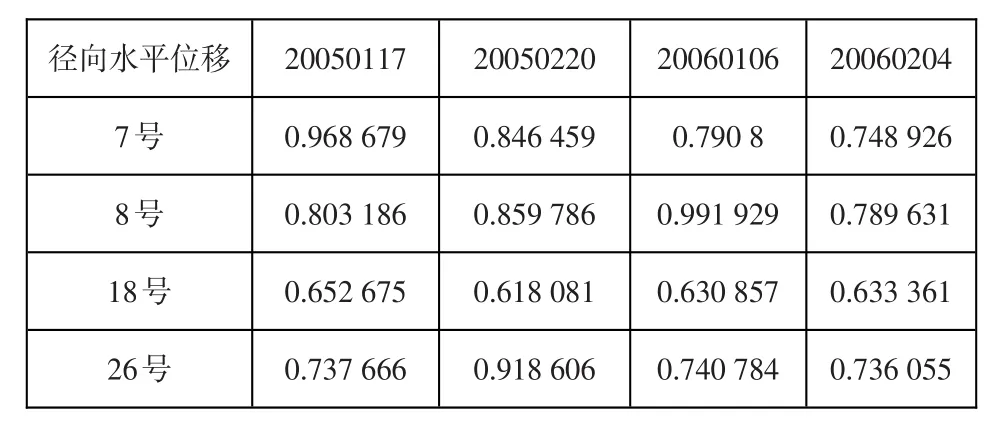
表5 徑向水平位移下屬因子安全度值Table 5:Safety values of subordinate factors of the radial hori?zontal displacement

依據大壩監測資料，建立監測資料相關矩陣進行主成分分析，可得底層因子相對于上層因子安全度的權重。

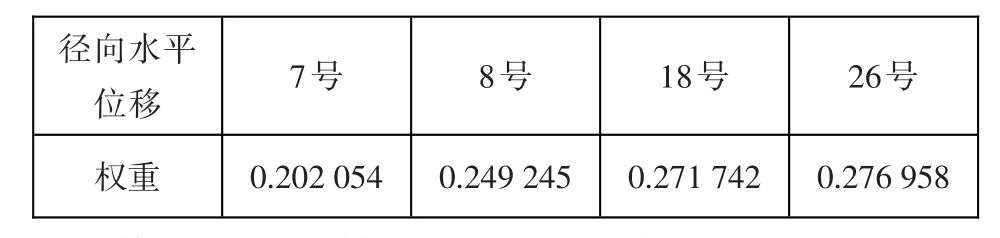
表6 徑向水平位移下屬因子權重Table 6:Weights of subordinate factors of the radial horizontal displacement

依據上述計算結果，兩者綜合考慮即可得徑向水平位移因子安全度值。

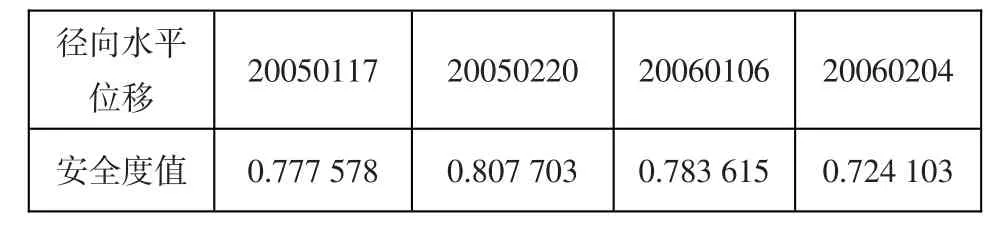
表7 徑向水平位移因子安全度值Table 7:Safety values of the radial horizontal displacement factor

同理可得切向水平位移因子和垂直位移因子安全度值。

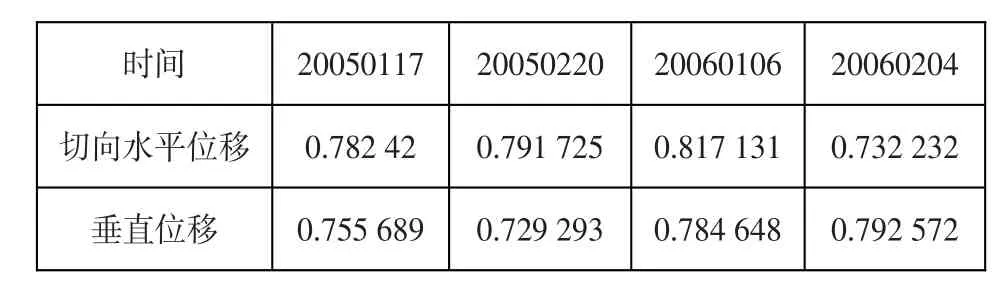
表8 切向水平位移因子及垂直位移因子安全度值Table 8:Safety values of the tangential horizontal displacement fac?tor and vertical displacement factor

在進行變形因子安全度求解時，徑向水平位移和垂直位移采用不同的回歸模型，回歸參數不同，如果采用PCA法進行求權的話，很難選擇數據，也不能保證結果的可靠性，因此采用層次分析法進行求權工作，結果見表9。

表9 徑向水平位移因子、切向水平位移因子、垂直位移因子權值Table 9:Weights of radial horizontal displacement factor,tan?gential horizontal displacement factor and vertical displace?ment factor

最后可得變形安全度值。

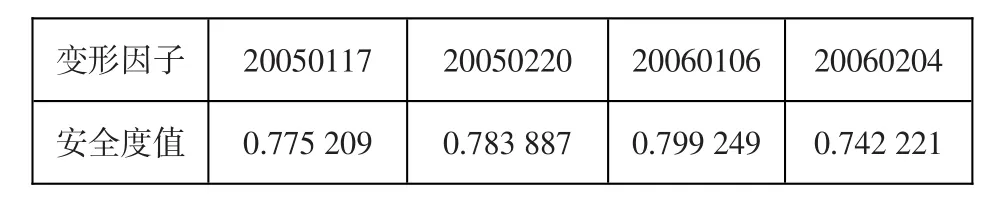
表10 變形因子安全度值Table 10:Safety value of the deformation factors

該大壩已運行30余年，其工作狀態基本正常，處于正常可控范圍之內。從表10計算結果中可看出，大壩在2005、2006年1、2月份氣溫較低、水位較低的不利運行工況下，安全度值處于基本正常水平，與大壩實際監測結果相符，與傳統分析方法結果相符，證明本文方法具有一定的可行性。

3 結語

神經網絡方法應用于大壩安全評價具有其不可比擬的優勢，但現有評價方法無法為其提供學習樣本。本文提出了一種新的大壩安全評價方法，實現了傳統安全度評價值的量化，以及從底層因子開始層層向上，最終判斷大壩整體安全度的過程，為神經網絡應用于大壩安全評價提供了可能。另外，在此基礎上進行了實例計算，所得結果與常規方法所得結果相符，與實際情況相符，證明該方法具有一定的可行性，將神經網絡應用于大壩安全度評價領域是可行的。■

[1]吳中如，沈長松，阮煥祥.水工建筑物安全監控理論及其應用[M].南京:河海大學出版社，1990.

[2]吳中如，朱伯芳.三峽水工建筑物安全監測與反饋設計[M].中國水利水電出版社，1999：81～104.

[3]汪培莊.模糊集合論及其應用[M].上海科學技術出版社，1983：201～224.

[4]黃健元.模糊集及其應用[M].寧夏人民教育出版社，1999：15～35.

[5]趙斌，吳中如.BP模型在大壩安全監測預報中的應用[J].大壩觀測與土工測試，1999,23(6).

[6]楊杰，吳中如，顧沖時.大壩變形監測的BP網絡模型和預報研究[J].西安理工大學學報，2001,17(l):25～29.