偏最小二乘法（PLS)在體育科研中的應用與實踐

李江華，范葉飛，劉文鋒

1 前言

計算機的普及與發展使得對海量數據進行分析與處理成為可能，與此相適應，采用“系統論”的方法從系統、整體的角度進行研究也日漸成為 21世紀科學研究的主流趨勢。體育科研也不例外，尤其是運動人體科學、基因組學、蛋白質組學、代謝組學等主流的系統生物學研究方法已開始頻繁用于相關的研究中。由于對系統性和整體性的追求，系統論指導下的研究方法往往會產生大量的數據，要想解讀如此復雜的信息，或者說從中提取有用的信息，就必須借助以計算機信息技術為基礎發展起來的模式識別技術。偏最小二乘法 （PLS)是 20世紀 80年代才發展起來的一種新型的模式識別方法，它集多元線性回歸法（MLR)和主成分分析法 （PCA)的基本功能于一體[7]。在高維數據處理中，如果樣本類別已知，PLS不但比傳統降維方法“PCA”的降維效果更好，而且以此為基礎發展起來的偏最小二乘法判別分析 （PLS-DA)也比傳統的線性判別分析 （LDA)具有更好的預測識別能力[10，12]；另外，PLS進行降維的同時還可以輕松實現“奇異樣本”的發現與剔除和自變量因子 （各觀測指標)的重要性程度分析，而其他類似的數據處理方法功能相對比較單一，難以同時實現這些分析。因其對高維度數據強大的處理能力，PLS已在生物信息學、藥學、社會科學等領域得到了廣泛的應用，而在體育界，PLS的研究與應用相對緩慢，其功能還有待于更多的研究與開發。為此，本研究以參加第 15屆亞運會中短距離比賽的中國游泳隊男運動員的核磁共振 （NMR)數據為例，通過與 SPSS軟件中常用的 PCA降維及 LDA數據處理效果進行比較，闡述 PLS分析的優越性以及如何利用PLS進行降維、發現奇異樣本、分析自變量因子 （各觀測指標)的重要性程度和實現判別分析。

2 研究方法

2.1 數理分析

通過簡單分析 PLS的計算過程，闡述 PLS分析的基本原理與思路。

2.2 案例分析

利用 SIMCA-P 10.0軟件，以參加第 15屆亞運會中短距離比賽的中國游泳隊男運動員的核磁共振 （NMR)數據為例，闡述 PLS分析的基本功能與實現過程，并通過與SPSS軟件中的 PCA降維及 LDA數據處理效果進行比較，闡述 PLS分析的優越性。

2.2.1 取樣與測試

亞運會賽前一個月內，每周 1次，連續收集運動員晨尿 3次。運動員根據亞運會的比賽成績是否進入前 8名，分為決賽運動員組 （FG)和非決賽運動員組 （NF)，其中， FG樣本 19個，NF樣本 30個。所有樣品進行預處理后，在500.13MHZ磁場共振頻率下進行一維核磁共振氫譜（1H NMR)測試。

2.2.2 數據處理

為了消除核磁共振采集信號過程中壓水峰所造成的影響，去除了水峰和尿素峰附近 6.2～4.6 ppm這一區段（圖 1)。然后對 10～0.2 ppm進行分段積分，每段為 0.02 ppm，結果從每個樣本的1H NMR獲得了 409個相應的積分數據[1，2]。積分數據經過常規歸一化處理后，即可導入SIMCA-P 10.0軟件，進行 PLS分析，計算公式如下：

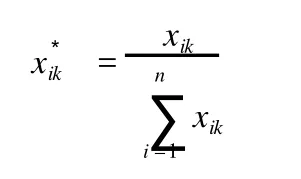
式中，xik為第k個樣本，i區段的原始積分數據；為標準化以后的數據。

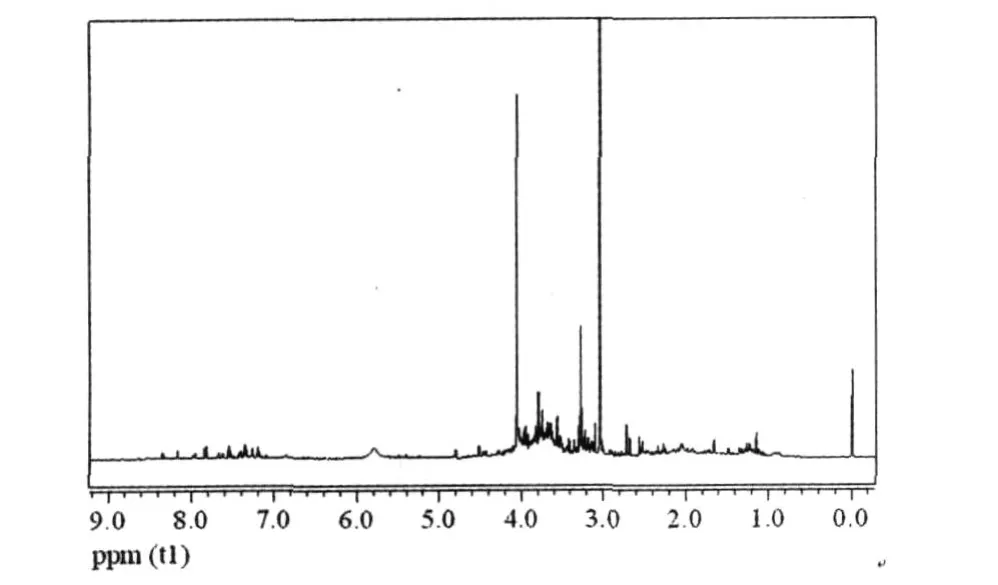
圖 1 傅立葉變換后的一維核磁共振氫譜圖

3 偏最小二乘法（PLS)分析的基本原理

與主成分分析一樣，PLS也是通過提取主成分的方法達到降維的目的，即將原變量進行轉換，從而產生少數幾個新變量（主成分)，這些新變量是原變量的線性組合，同時，這些新變量要盡可能多地表征原變量的數據結構而盡量少丟失信息，并且新變量即主成分互不相關，即正交。如果從數學上進行解釋，即為：設有p個原始指標（x1，x2， x3，Λ，xp)，用來對n個樣本進行評價，則共有np個數據。提取主成分的目的是要將這些原始指標組合成新的相互獨立的綜合指標：y1，y2，y3，L，yp，這些綜合指標表現為原始指標的線性函數[3]：

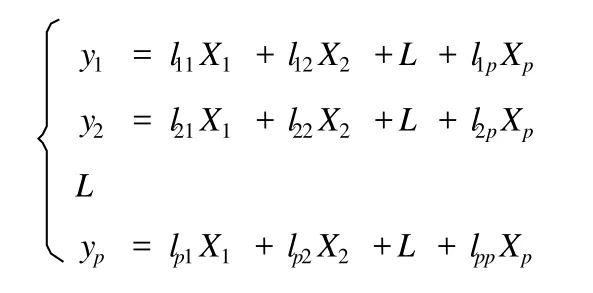
PLS與主成分分析不同點在于主成分分析法只考慮一個自變量矩陣，而偏最小二乘法還有一個因變量矩陣，在各自提取主成分的同時還要考慮兩個矩陣之間相關關系。因此，PLS分析的基本思路可以概括為：“同時提取因變量主成分和自變量主成分并使兩者的相關性達到最大”。具體要求：1）各主成分必須是原變量的線性組合，為了盡可能多地攜帶變量的變異信息，要求它們的方差達到最大；2）為了使自變量成分對因變量成分有最大的解釋能力或預測能力，要求兩者的相關性達到最大[4]。從數學上進行解釋，即為：設有因變量Y={Y1，Y2，…，Ym}和自變量集合X={X1，X2，…，Xm}，為了研究Y與X間的統計關系，首先在X與Y中提出主成分t1和u1，PLS方法在提取這兩個主成分時要求同時滿足：1)t1和u1盡可能多地攜帶它們各自數據表中的變異信息；2)t1和u1的相關程度能夠達到最大[9]。綜合以上兩點要求，可以歸結為使兩者的協方差達到最大[4]。

4 偏最小二乘法（PLS)分析的基本功能

4.1 降維與發現奇異樣本

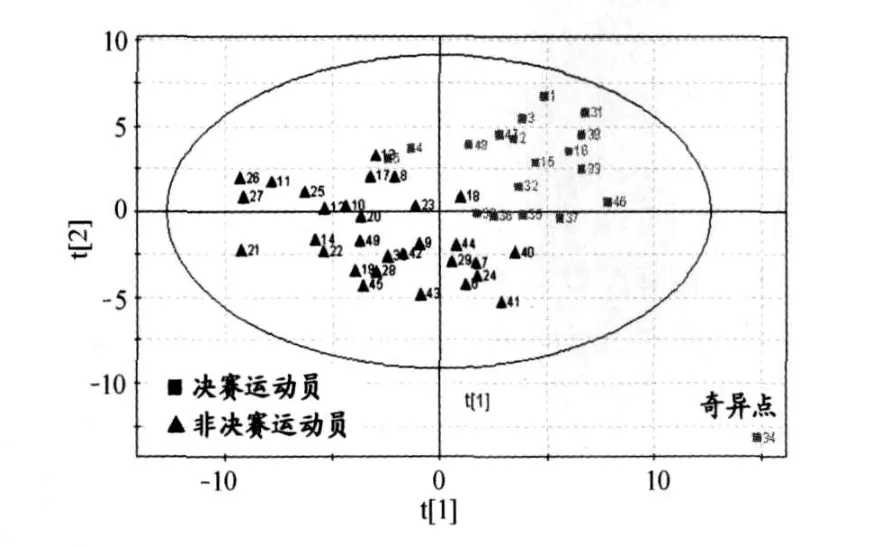
圖 2 偏最小二乘法（PLS)降維效果圖（t1 vs t2)

PLS分析的中心目的是降維，以排除眾多信息共存中相互重疊的信息。與傳統降維方法相比，由于考慮了樣本的類別信息，其后續分類效果較好，并且往往只需提取較少的幾個主成分進行分析即可實現對總體的綜合評價。這一優點使得數據可視化成為可能，通過 PLS的二維或三維主成分散點圖的直觀表征，人們可以輕易地對樣本類別信息進行觀察與分析，有利于進一步挖掘數據的內在特征。經 PLS降維后，第一成分t1對第二成分t2的散點圖顯示(圖2) ,決賽運動員組( FG)和非決賽運動員組(NF)樣本各自聚集，分離性較好。這一結果表明，高水平運動員尿液核磁共振 （NMR)數據能在一定程度上反映運動員之間競技水平的差異，利用 NMR進行尿液分析實現對高水平運動員的狀態監控具有一定的可行性。

同時，在實驗或觀測過程中難免會有偶然誤差產生，由此引起某些樣本的數據出現異常，PLS在實現降維的過程中還可以實現異常數據的發現與剔除。其基本原理是通過第i個樣本點對第h個成分th的貢獻率t2hi來發現樣本點集合中的異常數據[6]。

在 PLS模型中，定義樣本點i對成分t1，t2，…，tm的累計貢獻率為：

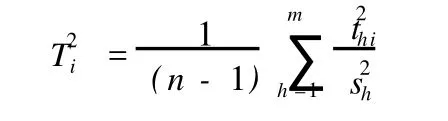
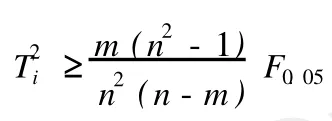
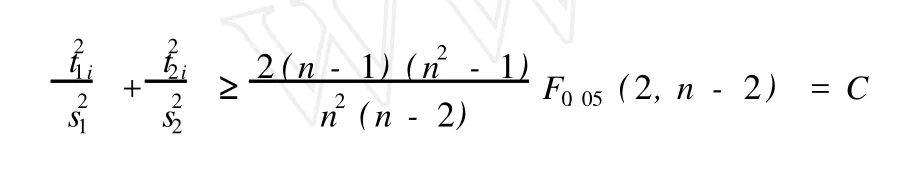
上式表示的圖形為一橢圓，在t1/t2二維平面圖上，可以做出 T2橢圓圖。如果所有的樣本點都落在橢圓區內，則認為所有樣本點的分布是均勻的，落在橢圓區外的樣本點為異常點[6]。

圖 2中的絕大多數樣本點都落在橢圓區內，第 34號樣本落在橢圓區外，可見本研究的案例中，運動員的樣本點總體上是分布均勻的，只有 34號樣本屬于奇異值。至此，一方面，在建模時或進一步進行數據處理時應將此樣本剔除；另一方面，還可以據此對實驗過程進行回顧，查找奇異值產生的原因。剔除 34號樣本后，重新進行 PLS的結果如圖 3所示，相對于圖 2，決賽運動員組 （FG)和非決賽運動員組 （NF)樣本得到了更好的分離效果。而主成分分析 （PCA)的降維效果則明顯較差 （圖 4)，決賽選手和非決賽選手的樣本分布散亂，相互交錯，沒有出現明顯的分離。

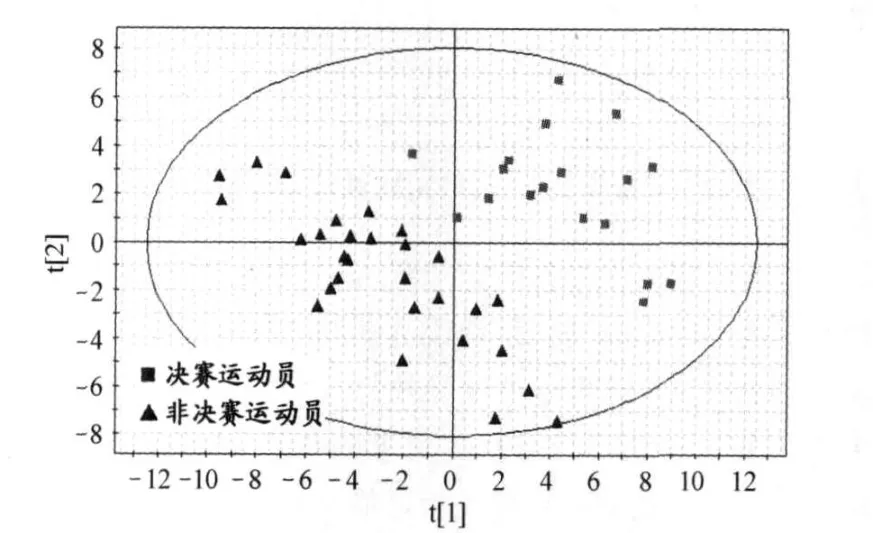
圖 3 剔除奇異點后的偏最小二乘法（PLS)降維效果圖（t1 vs t2)

4.2 自變量因子 （各觀測指標)的重要性程度分析

PLS分析主要用于多維數據的降維，需要進行 PLS的數據往往含有多個觀測指標 （也稱自變量因子)，如本研究所分析的案例，從每個樣本的1H NMR就產生了 409個相應的數據，即有 409個自變量因子。那么，這么多的自變量因子對因變量的解釋能力都相等嗎?因此，在對多維數據進行分析的過程中，往往需要找出對因變量的解釋能力較強的自變量因子，即重要性較高的觀測指標進行進一步分析。PLS分析中，觀測指標的重要性程度可以用變量投影重要性指標VIPj（variab le importance in p rojection，V IP)來量化。從 PLS建模過程可知，若所提取的成分th對Y的解釋能力越強，而自變量因子xj在構造th時又起到了相當重要的作用，則xj對Y的解釋能力就越大。所以，對于自變量因子x，可計算其重要性指標VIP[8]：

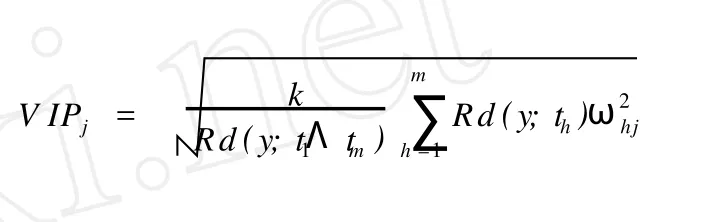
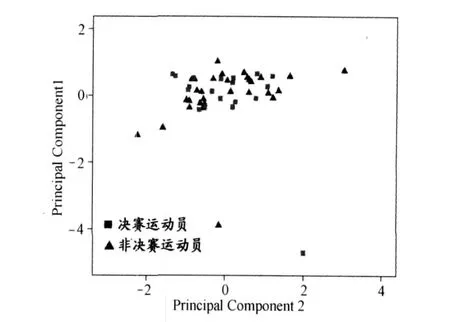
圖 4 主成分分析（PCA)降維效果圖（PC1 vs PC2)

通過對運動員尿液樣本的1H NMR所產生的 409個自變量因子的VIPj進行計算和排序，1H NMR譜中對運動員之間競技水平差異解釋能力較強的各區段及其所代表的代謝產物如表 1所示，對這些代謝產物的進一步的分析與討論可見筆者前期發表的相關文獻[11，12]。

表 1 對競技水平差異解釋能力較強的1 H NM R各區段及其所代表的代謝產物一覽表

4.3 實現判別分析 （PLS-DA)

偏最小二乘法判別分析 （partial least squares-discrim iannt analysis，PLS-DA)是基于 PLS回歸的一種判別分析方法，由于在構造因素時考慮到了輔助矩陣以代碼形式提供的類成員信息，因此，比傳統的判別分析法具有更高效的鑒別能力，也使出現假陽極鑒別的概率有所降低[5]。其核心思想是將測試的樣本人為地分為“訓練集”和“預測集”，其中，“訓練集”用來訓練建模，“預測集”則用來檢驗所建模型的預測能力，具體判別過程如下：

表 2 偏最小二乘法判別分析（PLS-DA)與線性判別分析（LDA)對運動員預測集樣本類別的識別結果比較一覽表

1.利用“訓練集”數據對計算機進行訓練 （建立模型)。例如，對于兩類的情況，在訓練集中，有一些樣本屬于 A類，另外一些樣本屬于 B類，然后教給計算機，建立分類變量與觀測數據間的 PLS回歸模型。

2.根據所建立的 PLS模型，輸入“預測集”各樣本的觀測數據，計算機計算識別這些“未知樣本 （不輸入這些樣本的分類信息)”的類別。

本研究的案例共有樣本 49個，其中的 33個樣本 （約2/3)為訓練集，16個樣本 （約 1/3)為預測集。計算機經過訓練之后，對預測集樣本類別的識別結果如表 2所示：3個樣本的類別識別錯誤，13個樣本的類別識別正確，總判別正確率為 81.25％。而在所有的數據條件完全相同的情況下，線性判別分析的結果則相對較差，總判別正確率僅為68.75％（表 2)。

5 結論

偏最小二乘法 （PLS)對高維度數據具有強大的處理能力。在體育科研中，同樣可以根據 PLS分析的基本原理，利用 PLS進行降維、發現異常數據、分析自變量因子 （各觀測指標)的重要性程度和實現判別分析，并且在已知樣本類別的條件下，PLS比傳統降維方法“PCA”及“LDA”具有更好的數據處理效果。

[1]李江華，劉承宜，徐曉陽，等.2006多哈亞運會短距離游泳男運動員志愿者代謝組學研究[J].體育科學，2008，28（2)：42-46.

[2]李江華，劉承宜，沙海燕，等.高水平男子中短距離游泳成績預測代謝組學模型[J].體育學刊，2010，17（4)：103-106.

[3]聶馥霖.淺談統計綜合評價中主成分分析法的應用[J].陜西綜合經濟，2007，（5)：46-48.

[4]錢國華，茍鵬，程陳峰，等.偏最小二乘法降維在微陣列數據判別分析中的應用[J].中國衛生統計，2007，24（2)：120-123.

[5]楊忠，任海青，江澤慧，等.PLS-DA法判別分析木材生物腐朽的研究[J].光譜學與光譜分析，2008，28（4)：793-796.

[6]楊杰，方俊，胡德秀，等.偏最小二乘法回歸在水利工程安全監測中的應用[J].農業工程學報，2007，25（3)：136-140.

[7]張琳，張黎明，李燕，等.偏最小二乘法在傅里葉變換紅外光譜中的應用及進展[J].光譜學與光譜分析，2005，25（10)：1610-1613.

[8]周強，歐陽一鳴，胡學鋼，等.數據挖掘中應用偏最小二乘法發現異常值[J].微電子學與計算機，2005，22（1)：25-27.

[9]周秀平，王文圣，曾懷金.偏最小二乘與人工神經網絡耦合模型在酸雨 pH值預測中的應用[J].水利水電科技進展，2006，26 （4)：50-52.

[10]BOULESTEIX A L，PORZEL IUSC，DAUM ERM.M icroarray-based classification and clinical p redictors：on combined c lassifiers and additional p redictive value[J].B ioinformatics，2008，24（15)： 1698-706.

[11]L IJH，L IU TCY，YUAN JQ，etal.Performance-enhancing photobiomodu lation[J].Laser Su rgM ed，2007，39（S19)：68.

[12]NGUYEN D，ROCKE D M.Tumor classification by partial least squares usingm icroarray gene exp ression data[J].B ioinformatics， 2002，18（1)：39-50.