基于Elman 網絡的傳遞對準容錯聯合濾波器設計與仿真

胡健，馬大為，程向紅，周百令

(1.南京理工大學 機械工程學院，江蘇 南京210094;2.東南大學 儀器科學與工程學院，江蘇 南京210096)

在機翼撓曲變形不可忽略的情況下，采用速度加姿態匹配的方法可進行快速傳遞對準［1-2］。但用于快速傳遞對準的Kalman 濾波器的階數將高達21維，故需要進行大處理量的濾波計算，這將導致快速傳遞對準所要求的快速濾波更新率得不到滿足。文獻［3］采用聯合Kalman 濾波器解決這一問題。但在聯合濾波器中，對應于各子濾波器和主濾波器的信息分配系數β1，…，βm的取值決定了聯合濾波器的性能，而文獻［3］并未對信息分配系數進行優化。此外，Kalman 濾波器對系統模型和噪聲等不確定性因素的魯棒性能較差。文獻［4］采用強跟蹤Kalman濾波器來提高系統魯棒性，但是該方法在克服濾波發散的過程中，破壞了濾波器的最優條件，導致濾波精度降低。文獻［5］推導了一種能根據每個狀態噪聲的變化來調節誤差協方差陣中相應的漸消因子的強跟蹤濾波算法，進一步提高了強跟蹤Kalman 濾波器的自適應能力，但濾波精度并未得到明顯改善。

本文綜合考慮以上各因素，提出采用聯合強跟蹤Kalman 濾波器進行快速傳遞對準。提出了一種基于模糊加權系數的誤差方差陣估計方法，以提高傳統強跟蹤Kalman 濾波算法的精度，并在此基礎上設計了聯合強跟蹤Kalman 濾波器的結構和算法，并利用改進的Elman 網絡進行信息分配系數的自適應調節。仿真結果表明，在載機進行搖翼機動的情況下，應用聯合強跟蹤Kalman 濾波器進行快速傳遞對準，不僅大大減小了計算量，提高了濾波器的解算速度，而且實現了融合信息在各子系統中的自適應分配，提高了系統故障魯棒性和狀態估計精度。

1 改進的強跟蹤Kalman 濾波算法

1.1 模糊加權系數的引入

在強跟蹤Kalman 濾波算法中，誤差方差陣的估計公式［4］為

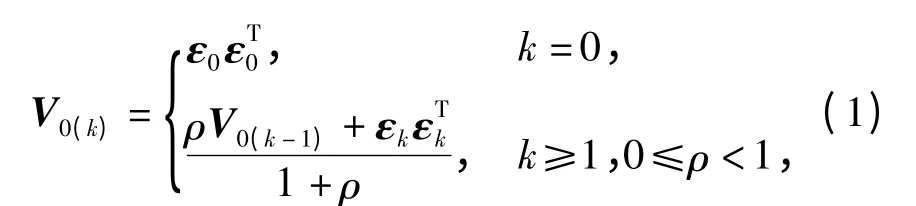
取歷史均方誤差信息矩陣V0(k)的對角線元素構成向量Vs(k)，簡記為Vs(k)=diag［V0(k)］.同理，取當前殘差信息矩陣εkεTk的對角線元素構成向量Vε(k)，簡記為Vε(k)=diag［εkεTk］.相似系數rij表示2個樣本xi與xj之間的相似程度，它可以用數量積分法、夾角余弦法、距離法等確定。本文采用夾角余弦法計算向量Vs(k-1)和Vε(k)之間的相似系數rv(k)，即顯然，相似系數rv(k)的大小反映了當前殘差信息矩陣與歷史信息陣V0(k-1)的相似程度。基于相似系數rv(k)，本文給出V0(k)估計公式V0(k)=(1 -γ)·根據相似系數rv(k)和狀態估計方差陣的跡tr(Pk-1)確定，本文稱之為模糊加權系數。

1.2 模糊加權系數的自適應調節

本文根據模糊理論對參數γ 進行在線調節，以提高濾波器性能。模糊自適應調節系統的輸入為當前時刻的相似系數rv(k)和前一時刻狀態估計方差陣的跡tr(Pk-1)，它們按照Gauss 隸屬度函數進行模糊化，系統的輸出按照重心法進行反模糊化。

當rv(k)較小，tr(Pk-1)也較小時，表明當前信息陣與歷史信息陣的相似程度低，且前次濾波精度較高，歷史信息陣的估值較準，則γ 應取較小值，以減小對當前信息陣的利用程度;當rv(k)較小，tr(Pk-1)較大時，表明當前信息陣與歷史信息陣的相似程度低，且前次濾波精度較低，歷史信息陣的估值不太準，則γ 應取較大值，以加大對當前信息陣的利用程度;其余依此類推，從而得到系統的模糊推理規則如下:

1)如果rv(k)很小且tr(Pk-1)很小，則γ 較小;

2)如果rv(k)很小且tr(Pk-1)較小，則γ 較小;

3)如果rv(k)很小且tr(Pk-1)較大，則γ 較大;

4)如果rv(k)較小且tr(Pk-1)很小，則γ 較小;

5)如果rv(k)較小且tr(Pk-1)較小，則γ 較小;

6)如果rv(k)較小且tr(Pk-1)較大，則γ 較大;

7)如果rv(k)較大且tr(Pk-1)很小，則γ 較大;

8)如果rv(k)較大且tr(Pk-1)較小，則γ 較大;

9)如果rv(k)較大且tr(Pk-1)較大，則γ 較小。

2 聯合強跟蹤Kalman 濾波器結構設計

本文針對速度加姿態匹配快速傳遞對準設計了一個聯合強跟蹤Kalman 濾波器，其結構如圖1所示。該濾波器是一種兩級數據融合結構，具有2 個子濾波器，分別為速度子濾波器和姿態子濾波器，前者使用主慣導的速度數據作觀測量，后者使用主慣導的姿態數據作觀測量，它們均采用改進的強跟蹤Kalman 濾波算法給出各自狀態變量的最優估計，再由主濾波器融合2 個子濾波器的輸出，給出2 個子濾波器共同狀態的全局最優估計.結構中改進的Elman 網絡用于將信息系數β1，β2，βm自適應分配到各子濾波器和主濾波器中。圖中，Pcv，，Pcθ，和Pcm分別為速度子濾波器、姿態子濾波器以及主濾波器對公共狀態變量的局部最優估計和誤差協方差陣;為Xc的全局最優估計;Pc為全局最優估計的誤差協方差陣;Qc為公共狀態的過程噪聲方差強度陣。

圖1 快速傳遞對準聯合強跟蹤Kalman 濾波器結構Fig.1 Structure of federated strong tracking Kalman filter for rapid transfer alignment

3 聯合強跟蹤Kalman 濾波器信息分配

聯合濾波器的信息分配原則對于提高系統的可靠性、精度等具有重要意義，Carlson［7］最先提出的信息分配原則是固定比例的，考慮到在實際的高動態導航環境中，各子濾波器的性能和估計質量都是不斷變化的，這時Carlson 提出的固定信息分配策略就不能夠滿足應用的需求了。文獻［8 -10］提出了不同的信息分配原則。文獻［8］利用局部濾波和全局濾波一步預測信息陣的跡之比作為信息分配系數，從而使聯合濾波局部濾波器的設計也成為最優。文獻［9］提出一種引入權衡因子的信息分配策略，能夠根據具體應用場合靈活調整局部濾波精度和容錯性。文獻［10］提出了一種基于子系統在不同環境下可能發生的故障概率的魯棒信息分配方法，對于提高子濾波器的抗干擾能力有一定的效果。雖然關于信息分配研究成果很多，但目前為止還沒有一個統一的認識。尤其是當發生傳感器故障時，怎樣通過信息分配提高具有反饋結構的聯合濾波器無故障子系統抗污染能力的問題，未引起足夠的重視，而這對于提高聯合濾波器的魯棒性和快速重構能力具有重要意義。

Elman 神經網絡［11-12］模型在前饋網絡的隱含層中增加一個承接層，作為一步延時算子，達到記憶的目的，從而使系統具有適應時變特性的能力，能直接反映動態系統的特性。因此，本文利用改進的Elman 網絡根據局部濾波器和主濾波器的實時動態性能來調整信息分配系數，可有效提高系統故障魯棒性和快速重構能力。

3.1 改進型Elman 網絡結構與訓練算法

標準Elman 網絡中自反饋增益α 是固定值，一般是根據經驗來選取，α 值選擇得不好會導致系統出現發散現象，而本文考慮把各α 當作連接權值投入到網絡的訓練中，從而實現自反饋增益系數的動態修正。此外，為了增加神經元對歷史數據的敏感程度，在原Elman 網絡中增加了輸出層關聯單元，以存儲輸出層的歷史數據，并反饋給輸出單元，設計了一個適于本系統的改進型Elman 網絡，其結構如圖2所示。改進后的Elman 網絡具有較高的收斂精度和較短的學習時間。設網絡的輸入層為r 個節點，隱層和隱層關聯單元為n 個節點，輸出層和輸出層關聯單元為m 個節點，則網絡的狀態空間表達式為

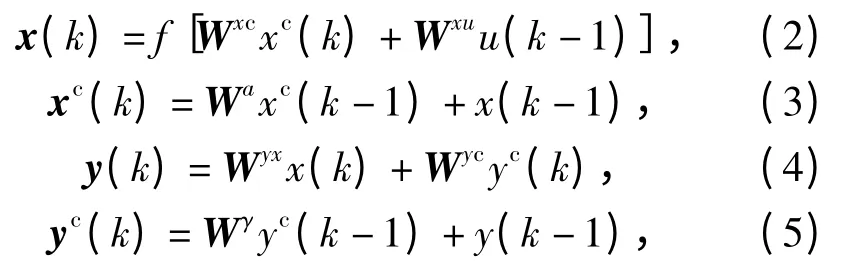
式中:Wxc，Wxu，Wyx，Wyc分別為隱層關聯單元到隱層，輸入單元到隱單元，隱單元到輸出單元及輸出層關聯單元到輸出單元的權矩陣;Wα=diag［α1，…，αn］，Wγ=diag［γ1，…，γn］為自反饋增益矩陣;f 為Sigmoid 函數。

設第k 步系統的實際輸出為yd(k)，定義誤差函數為將E 對連接權Wγ，Wyx，Wyc，Wα，Wxu，Wxc分別求偏導，由梯度下降法可得Elman 網絡的學習算法為

圖2 改進型Elman 網絡結構Fig.2 Structure of improved Elman network

3.2 基于改進型Elman 網絡的信息系數分配方法

將第i 個子濾波器的估計誤差協方差陣Pi進行特征值分解，即Pi=LΛiLT，其中Λi=diag{λi2，…，λiN}，定義第i 個子濾波器的精度因子Ei=trΛi，它反映了第i 個子濾波器的濾波精度。定義第i 個子濾波器的故障因子ρi(k)=‖Zi(k)-Hi(k)Xi(k，k-1)‖，它反映了第i 個子濾波器的故障程度。令所有子濾波器的Ei，ρi和主濾波器的Em構成Elman網絡的輸入向量u={E1，ρ1，…，El，ρl，Em}T，令所有子濾波器和主濾波器的信息分配系數βi構成Elman網絡的輸出向量y={β1，…，βl，βm}T，則利用訓練好的Elman 網絡就可以進行信息分配系數自適應調節。根據精度越低，故障程度越大，分配的信息分配系數越大的原則［8-9］，并結合聯合Kalman 濾波器的仿真結果給出網絡訓練樣本，進行離線訓練。

為保證信息分配系數滿足信息守恒原理，再對Elman 網絡的輸出進行修正

4 聯合強跟蹤Kalman 濾波器算法設計

4.1 聯合濾波算法流程

結合圖1，本文提出聯合強跟蹤Kalman 濾波算法如下:

1)給定初值

初值包括濾波估計初值，協方差陣P0，系統協方差陣Q0以及系統信息分配系數向量初值;

2)信息分配

利用改進的Elman 網絡解算出新的信息分配系數向量，自適應調整信息分配系數，公共狀態變量信息按信息守恒原理在各濾波器間進行分配

3)子濾波器進行時間更新和測量更新

①時間更新:各子濾波器根據各自的狀態方程進行時間更新，算法如下

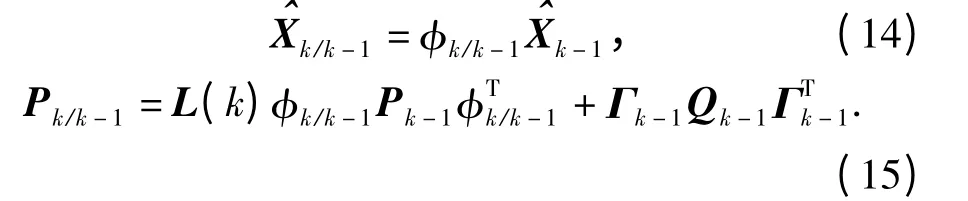
②測量更新:當有量測值時，各子濾波器根據量測值進行修正，即進行量測更新，算法如下

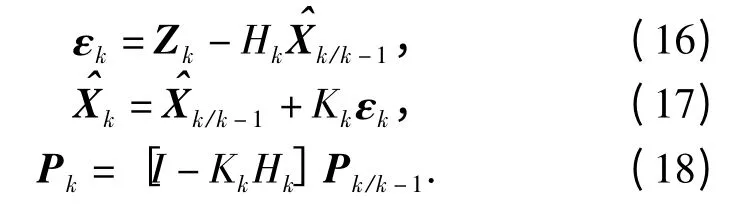
4)主濾波器時間更新

主濾波器根據自己的狀態方程進行時間更新，算法如下

式中:L(k)為時變的漸消矩陣;λi(k)≥1，i =1，…，n，為n 個時變的漸消因子，

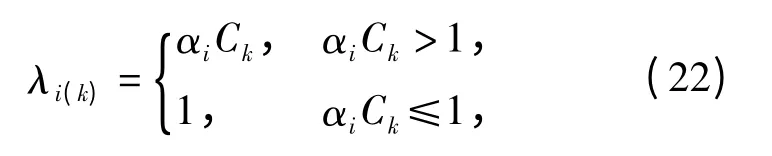
5)信息全局融合

在各濾波器計算出各自的局部估計之后，由主濾波器把各濾波器的公共狀態和Pcm按照(23)式和(24)式進行信息的全局融合，得到全局估計信息

融合后，返回步驟2)作循環。

4.2 聯合濾波算法的簡化

應用模糊方法進行模糊加權系數的計算較為麻煩。在實際應用中，可以預先進行各種歸一化輸入量的模糊加權系數計算，并將計算結果存入計算機。在實時計算中只要將輸入量按照同樣的方法進行歸一化，然后通過查表即可得到模糊加權系數的量值，而不必進行復雜的計算。相似系數本身在［0，1］內，無需再進行歸一化;對于tr(Pk-1)，可事先根據導航子系統濾波的實測值或理論計算值，得到導航子系統精度最差值，即tr(Pk-1)的最大值，將子濾波器的tr(Pk-1)除以最大值，由此可將tr(Pk-1)的歸一化值約束在［0，1］內，從而完成歸一化過程。

5 系統仿真

假定載機進行搖翼機動，橫滾角的最大偏角為20°，機動周期為6 s，飛行速度200 m/s.子慣導陀螺常值漂移1°/h，隨機漂移1°/h;加速度計常值偏置500 ×10-6，隨機誤差100 ×10-6.主濾波器初始信息分配系數為0.2，2 個子濾波器的初始信息分配系數為0.4，Elman 網絡輸入層節點數為5，隱層節點數取為8，輸出層節點數為3，從而形成5 -8 -3 的網絡結構，學習步長均選為0.15.

1)假定速度觀測噪聲是以二階馬爾可夫為隨機過程的有色噪聲。分別應用聯合強跟蹤Kalman濾波器和集中Kalman 濾波器對系統狀態進行估計。圖3給出了2 種濾波器的東、北、天向失準角估計誤差(δφe，δφn，δφu)對比曲線，表1列出了2 種濾波器的對準精度。通過比較可以看出，聯合強跟蹤Kalman 濾波器在10 s 內對東、北、天向失準角的估計誤差可以收斂到3'以內，估計精度比集中Kalman 濾波器要高，而對安裝誤差角和機翼撓曲變形角的估計精度比集中Kalman 濾波器要提高一個數量級。

圖3 觀測噪聲為有色噪聲時的2 種方法比較Fig.3 Comparison of two methods under coloured noise

2)假設速度傳感器在10～15 s 之間發生故障而后恢復正常。使用本文的方法與使用集中Kalman 濾波器對東、北、天向失準角估計誤差對比曲線，如圖4所示。從圖4中可以看出，使用聯合強跟蹤Kalman 濾波器時，速度傳感器恢復正常后，濾波器迅速恢復正常工作，而使用集中Kalman 濾波器，濾波結果出現發散。這表明，使用本文的方法，系統對故障的魯棒性較好。

表1 使用不同濾波器進行對準的對準精度對比(10 s 內)Tab.1 The comparison of alignment accuracy of two different filter (in 10 s)

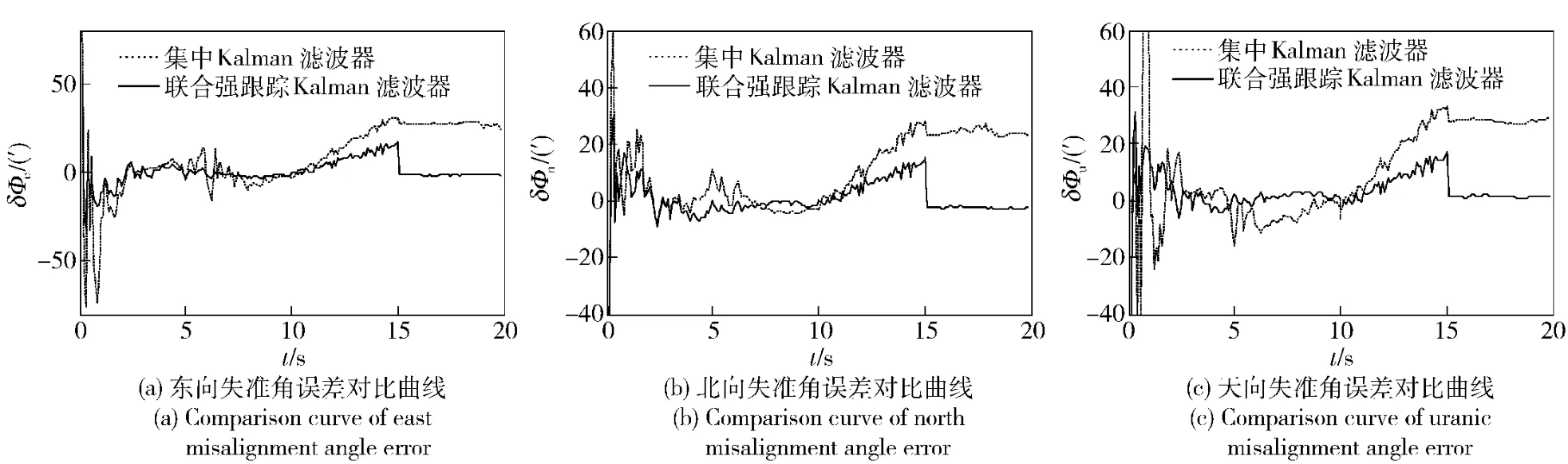
圖4 速度傳感器故障時的2 種方法比較Fig.4 Comparison of two methods when speed sensor malfunctions

由此可見，本文設計的聯合強跟蹤Kalman 濾波器顯著減少了有色噪聲對濾波器誤差特性的干擾，且具有較強的故障魯棒性，提高了系統狀態估計精度和抗干擾能力，并大大減小了計算量，提高了濾波器的解算速度。

6 結論

本文提出了一種適用于快速傳遞對準的聯合強跟蹤Kalman 濾波器，它利用模糊加權系數對誤差方差陣進行估計以提高傳統STF 的濾波精度，并利用改進的Elman 網絡進行信息分配系數的自適應調節。仿真結果表明該算法可以降低系統模型和噪聲不確定性的影響，提高系統故障魯棒性和對準精度，并大大減小計算量，提高解算速度。

References)

［1］Shortelle K J，Graham W R，Rabourn C.F-16 flight tests of a rapid transfer alignment procedure［C］∥IEEE Position Location and Navigation Symposium，Piscataway:IEEE，1998:379 -386.

［2］Joon Lyou，You-Chol Lim.Transfer alignment error compensator design based on robust state estimation［C］∥Transactions of the Japan Society for Aeronautical and Space Sciences，Tokyo:Japan:Society for Aeronautical and Space Sciences，2005:143 -151.

［3］GU Dong-qing，QIN Yong-yuan，PENG Rong，et al.Rapid transfer alignment using federated kalman filter［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2005，22(2):139 -143.

［4］付夢印，鄧志紅，張繼偉.Kalman 濾波理論及其在導航系統中的應用［M］.北京:科學出版社，2003.FU Meng-yin，DENG Zhi-hong，ZHANG Ji-wei.Kalman filtering theory and its application in the navigation system［M］.Beijing:Science Press，2003.(in Chinese)

［5］王新國，許化龍，李愛華.一種應用于星光觀測導彈姿態確定的強跟蹤濾波算法［J］.宇航學報，2008，29(3):873 -877.WANG Xin-guo，XU Hua-long，LI Ai-hua.A novel strong tracking EKF algorithm in application of missile attitude determination by star observations［J］.Journal of Astronautics，2008，29(3):873 -877.(in Chinese)

［6］程向紅，萬德鈞.分布式系統中捷聯慣性系統動基座對準研究［J］.中國慣性技術學報，2004，12(6):8 -12.CHENG Xiang-hong，WAN De-jun.Initial alignment of distributed strapdown inertial system on moving base［J］.Jounal of Chinese Inertial Technology，2004，12(6):8 -12.(in Chinese)

［7］Carlson N A.Federated Kalman filter simulation results［J］.Navigation，1994，41(3):297 -321.

［8］Jamshaid Ali，Fang Jian Cheng.SINS/ANS/GPS integration using federated Kalman filter based on optimized information-sharing coefficients［C］∥AIAA Guidance，Navigation，and Control Conf，Reston:AIAA，2005:6028 -6040.

［9］李金梁，吳訓忠，張宗麟.基于矩陣攝動理論的聯邦濾波信息分配方法［J］.系統工程與電子技術，2007，29(11):1940-1944.LI Jin-liang，WU Xun-zhong，ZHANG Zong-lin.Information-sharing approach to federated filtering based on matrix perturbation theory［J］.Systems Engineering and Electronics，2007，29(11):1940 -1944.(in Chinese)

［10］胡志強，張瑛，邱愷.基于故障概率的聯邦濾波魯棒信息分配方法［J］.系統工程與電子技術，2008，30(9):1801 -1804.HU Zhi-qiang，ZHANG Ying，QIU Kai.Robust information sharing scheme for federated filter based on fault probability［J］.Systems Engineering and Electronics，2008，30(9):1801 -1804.(in Chinese)

［11］HE Hai-tao，TIAN Xia.An improved Elman network and its application in flatness prediction modeling［C］∥Second International Conference on Innovative Computing，Information and Control，ICICIC 2007，Piscataway:IEEE Computer Society，2008:44 -48.

［12］REN Xue-mei，CHEN Jie，GONG Zhi-hao，et al.Approximation property of the modified elman network［J］.Journal of Beijing Institute of Technology，2002，11(1):19 -23.