一種用于自適應噪聲抵消的變步長LMS算法

李善姬

（延邊大學 工學院,吉林 延吉 133002）

一種用于自適應噪聲抵消的變步長LMS算法

李善姬

（延邊大學 工學院,吉林 延吉 133002）

為了提高LMS自適應濾波算法的性能,在分析已有變步長算法的基礎上進行了一些改進。改進算法用誤差信號的自相關來調節步長以實現對不相關噪聲的更好抑制,且采用先固定后變化的方法控制步長,兼顧了暫態和穩態性能。利用改進算法進行了自適應噪聲抵消的仿真實驗,結果表明,基于改進變步長LMS算法的自適應噪聲抵消器能有效抵制噪聲干擾,對含噪信號具有良好的消噪能力。

自適應濾波;噪聲抵消;LMS算法;變步長

1 引 言

自適應噪聲抵消器作為自適應濾波器的一種具體應用,能夠從背景噪聲中提取出有用信息,目前在語音處理、生物醫學等領域得到廣泛的應用。自適應噪聲抵消器的核心是自適應濾波器,其研究始于20世紀50年代末。目前,自適應濾波器最常用的算法結構為1965年Windrow提出的橫向結構LMS算法。由于該算法具有簡單、易于實時實現等優點,廣泛應用于系統辨識、信號處理、噪聲抵消等領域。收斂速度、時變系統跟蹤能力及穩態失調是衡量自適應濾波算法優劣的3個重要技術指標。傳統的固定步長LMS算法在收斂速度、時變系統的跟蹤能力和穩態失調之間的要求存在很大矛盾。為了解決步長因子與各方面性能之間的矛盾,有關變步長LMS算法的研究非常活躍。如文獻[1]提出了步長與均方瞬時誤差建立關系的算法,文獻[2]提出了基于箕舌線的變步長算法等。

本文在分析文獻[1]算法的基礎上,提出了一種改進的變步長LMS算法,并將改進算法應用到自適應噪聲抵消器中。算法分析及計算機仿真結果表明,利用改進算法的自適應噪聲抵消器在一定輸入信噪比下對含噪信號具有良好的消噪能力。

2 算法原理

2.1 基本LMS算法

基本LMS算法的迭代公式為

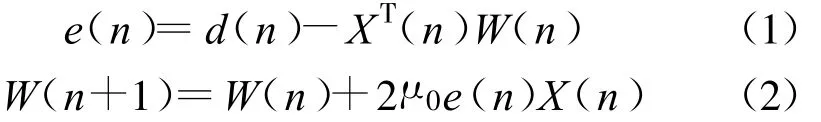
式（1）中,W（n）為自適應濾波器在時刻n的權向量;式（2）表示抽頭權向量更新公式,其中,μ0為控制收斂速度的常數,稱為步長因子。LMS算法收斂的條件為0<μ0<1/λmax,λmax是輸入信號自相關矩陣的最大特征值。

LMS算法具有計算簡單、易于實現等優點,因此在自適應濾波原理中得到了很好的應用。但由于輸入端不可避免地存在干擾噪聲,LMS算法將產生失調噪聲,干擾噪聲越大,引起的失調噪聲也就越大;減少步長因子 μ0,可以減少自適應濾波算法的穩態失調噪聲,提高算法的收斂精度。然而步長因子 μ0的減小,將降低算法的收斂和跟蹤速度。因此,這種固定步長的LMS算法在收斂速度、跟蹤速度及穩態失調噪聲等方面對步長因子 μ0值大小的選取要求是相互矛盾的。為了解決誤差和收斂間的矛盾,提高LMS算法的收斂性能,可以采用變步長的LMS算法。與固定步長的LMS算法相比,變步長算法的優越性在于:自適應算法的初始階段,誤差e（n）比較大,步長 μ（n）也相應較大,從而得到較快的收斂速度;當誤差逐漸減小時,步長 μ（n）變小,因此穩態誤差也很小。

2.2 改進的變步長LMS算法

為了克服步長因子與收斂速度及穩態失調誤差之間的矛盾,人們提出了各種各樣的變步長LMS自適應濾波算法或改進算法[1-4],如步長與均方瞬時誤差建立關系[1],基于箕舌線的變步長算法[2]等。

文獻[1]中的步長更新公式為

3 自適應噪聲抵消及其仿真

3.1 自適應噪聲抵消原理

自適應噪聲抵消技術是自適應信號處理理論的一種具體應用,它在具有噪聲背景下的信號提取與處理方面有著廣泛的應用,有關自適應噪聲抵消方面的研究[5-6]也廣泛進行。

自適應噪聲抵消系統的核心是自適應濾波器,自適應算法對其參數進行控制,以實現最佳濾波。因為這種方法比其它方法多用了一個參考噪聲作為輔助輸入,從而獲得了比較全面的關于噪聲的信息,因而能得到更好的降噪效果。特別是在輔助輸入噪聲與信號中的噪聲完全相關的情況下,自適應噪聲抵消法能完全排除噪聲的隨機性,徹底地抵消信號中的噪聲成分。但對不相關或相關性很弱的噪聲信號無能為力,這些噪聲信號不但不能被抵消,反而會對濾波器產生干擾,使算法效果受到影響。

自適應噪聲抵消器原理圖如圖1所示。

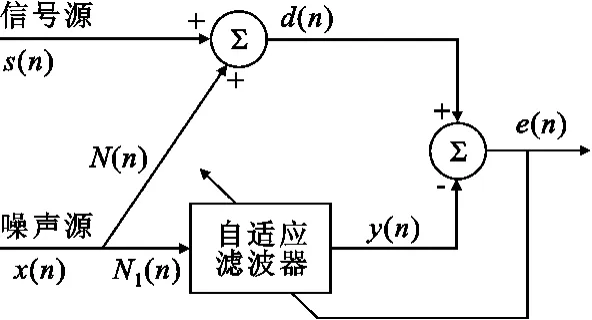
圖1 自適應噪聲抵消器原理圖Fig.1 Block diagram of an adaptive noise canceller

3.2 自適應噪聲抵消仿真

式中,N0的取值可根據初始步長 μ1和信號長度適當選取,本文中選擇N0=200。

圖2為采用文獻[1]算法（原算法）處理后自適應噪聲抵消器的輸出結果,圖3為采用本文算法（改進算法）處理后自適應噪聲抵消器的輸出結果,圖4為采用原算法處理后的均方誤差曲線,圖5為采用改進算法處理后的均方誤差曲線。

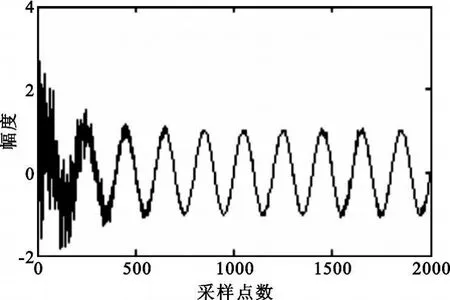
圖2 原算法處理結果Fig.2 Processing result of original algorithm

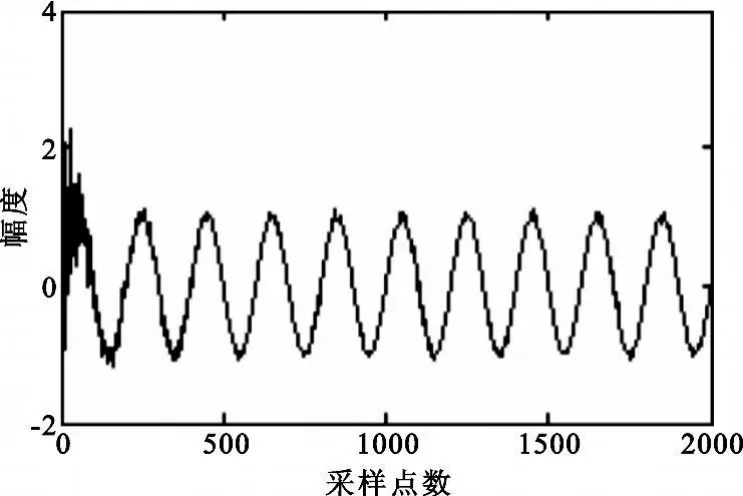
圖3 改進算法處理結果Fig.3 Processing resu lt of improved algorithm

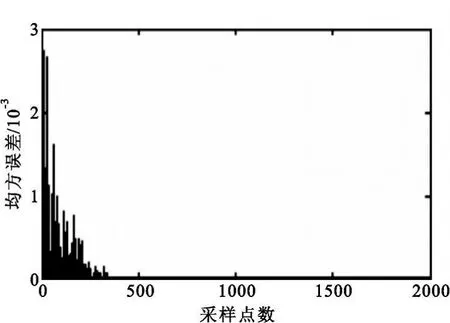
圖4 原算法的均方誤差Fig.4Mean-square error of original algorithm

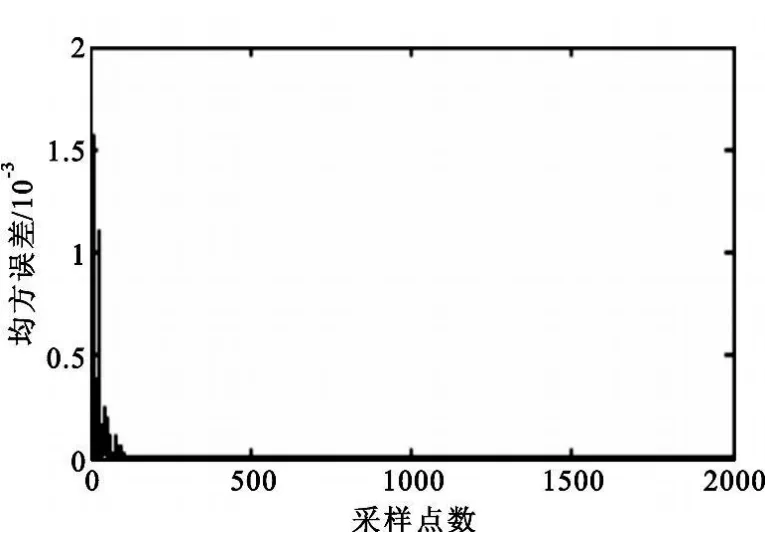
圖5 改進算法的均方誤差Fig.5Mean-square error of improved algorithm

從仿真結果可看出改進算法在初始階段有更好的處理效果。采用原算法時,輸入信噪比為-3.114 6 dB時輸出信噪比為9.897 2 dB,信噪比提高量為13.012 dB。采用改進算法時,輸入信噪比為-3.124 5 dB時輸出信噪比為16.29 dB,信噪比提高量是19.414 dB。仿真結果及分析表明,采用本文算法的自適應噪聲抵消器在一定輸入信噪比下對含噪信號具有良好的消噪效果。

4 結束語

自適應噪聲抵消系統的性能取決于自適應濾波算法。本文在分析文獻[1]提出的變步長LMS自適應算法的基礎上,對算法進行了一些改進。利用改進算法在MATLAB環境下對含噪信號進行了自適應噪聲抵消仿真實驗,仿真結果及算法分析表明改進算法具有更好的暫態性能,且對輸入端不相關噪聲的干擾具有更好的抑制能力。利用改進算法構成的自適應噪聲抵消器在一定輸入信噪比下得到了良好的消噪效果,但本文仿真只是在單頻正弦信號疊加高斯白噪聲的情況下進行的,對更復雜的實際情況還有待于進行進一步的研究。

[1] 高鷹,謝勝利.一種變步長LMS自適應濾波算法及分析[J].電子學報,2001,29（8）:1094-1097.

GAO Ying,XIE Sheng-li.The algorithm and analysis of variable-step LMS adaptive filtering[J].Acta Electronica Sinica,2001,29（8）:1094-1097.（in Chinese）

[2] 鄧江波,侯新國,吳正國.基于箕舌線的變步長LMS自適應算法[J].數據采集與處理,2004,19（3）:282-285.

DENG Jiang-bo,HOU Xin-guo,WU Zheng-guo.The algorithm of variable-step LMS adaptive filtering based on versiera[J].Journalof Data Acquisition&Processing,2004,19（3）:282-285.（in Chinese）

[3] 覃景繁,歐陽景正.一種新的變步長LMS自適應濾波算法[J].數據采集與處理,1997,12（2）:171-174.

QIN Jing-fan,OUYANG Jing-zheng.The new algorithm of variable-step LMS adaptive filtering[J].Journal of Data Acquisition&Processing,1997,12（2）:171-174.（in Chinese）

[4] 呂振肅,熊景松.一種改進的變步長LMS自適應算法[J].信號處理,2008,24（1）:144-146.

LV Zhen-su,XIONG Jing-song.The improved algorithm of variable-step LMS adaptive filtering[J].Signal Processing,2008,24（1）:144-146.（in Chinese）

[5] 蔣明峰,鄭小林,彭承琳.一種新的變步長LMS自適應算法及其在自適應噪聲對消中的應用[J].信號處理,2001,17（3）:282-286.

JIANG Ming-feng,ZHENG Xiao-lin,PENG Cheng-lin.The new algorithm of variab le-step LMS adaptive filtering and the application in adaptive noise cancellation[J].Signal Processing,2001,17（3）:282-286.（in Chinese）

[6] 李建奇,曹斌芳,彭元杰.一種自適應噪聲抵消系統的仿真與設計[J].噪聲與振動控制,2007,27（6）:76-79.

LI Jian-qi,CAO Bin-fang,PENG Yuan-jie.The simulation and design of adaptive noise cancellation system[J].Noise and Vibration Control,2007,27（6）:76-79.（in Chinese）

A Variable-Step LMS Algorithm for Adaptive Noise Canceller

LI Shan-ji
（College of Engineering,Yanbian University,Yanji 133002,China）

To improve the performance of LMS adaptive filtering algorithm,an improved variable-step LMS algorithm is proposed based on analysis of existing algorithms.With the autocorrelation step regulation of error signal,the improved algorithm realizes the better uncorrelated noise inhibiting ability.It gives consideration to both transient and steady performance by the step control method of first fixation and last variation.The simulation experiments of adaptive noise cancellation illustrate that the adaptive noise canceller based on modified variable step LMS algorithm has a better de-noising performance for the noise signal.

adaptive filtering;signal de-noising;LMS algorithm;variable step

TN911.7

A

10.3969/j.issn.1001-893x.2010.11.007

1001-893X（2010）11-0030-04

2010-07-16;

2010-08-30

李善姬（1959-）,女（朝鮮族）,吉林延吉人,1997年獲碩士學位,現為延邊大學工學院教授、碩士生導師,主要研究方向為信號與信息處理。

LI Shan-ji was born in Yanji,Jilin Province,in 1959.She

the M.S.degree in 1997.She is now a professor and also the instructor of graduate students in Engineering College of Yanbian University.Her research direction is signal and information processing.

Email:lishanji@ybu.edu.cn