金屬桿熱傳導的數值計算研究

康曉宇 吳惠 劉應開

(云南師范大學物理與電子信息學院 云南 昆明 650092)(昭通師專物理系 云南 昭通 657000)

1 引言

隨著計算機技術的發展和數值計算方法的改進，求解偏微分方程組等早期不能完成的任務現在逐步變為現實.在數值計算的各種軟件和軟件平臺中，MATLAB簡單易學且具有強大的可視化功能，為科學研究提供了極大的方便.特別是MATLAB中的PDE工具箱，無需編程則可直接求解具有特殊邊界條件的導熱問題，并將結果可視化，從而對物理過程和有關特征量的演化有一個直觀的認識.

在熱學中，熱傳導問題是一個基礎性的課題，對其進行研究有助于理解熱傳導的基本規律，澄清基本物理概念.在數學物理方法中，熱傳導問題是由熱傳導方程來描述.熱傳導方程的求解因邊界條件不同而難度各異.有的問題沒有嚴格的解析解，只能求得數值解；有的則存在嚴格的解析解，其解的形式可能是積分形式.也可能是級數形式，從這些解中很難準確知道溫度、熱流密度等物理量在空間的分布和隨時間的演化規律.本文利用MATLAB中的PDE工具箱求解兩類一維熱傳導問題，它們分別屬于第一類和第二類邊界條件.通過求解兩類問題中的溫度場、熱流密度分布與演化規律，揭示熱傳導的本質，從而澄清穩定態與平衡態的區別與聯系.

2 一維熱傳導方程

均勻金屬桿可看作一維傳熱系統.如圖1所示，桿的左端作為坐標原點，則右端的坐標為L，桿上各點的溫度T(x,t)滿足偏微分方程

(1)

其中a=κ/cρ，κ，c和ρ分別為金屬桿的熱導率、比熱容和密度.

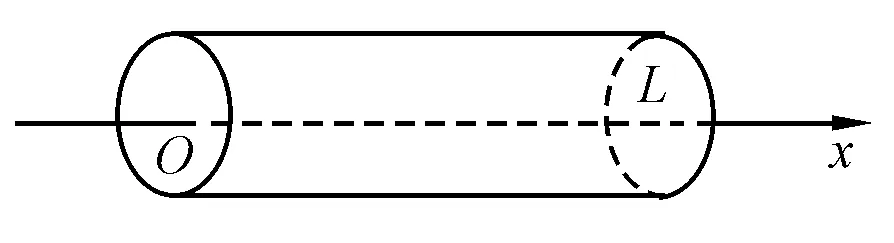
圖1 一維細桿熱傳導示意圖

3 兩類邊界條件的一維熱傳導問題

3.1 第一類邊界條件的一維熱傳導問題

長為L均勻鐵制金屬桿，桿的初始溫度為20℃，其左端與0℃的恒溫熱源接觸，右端與100℃恒溫熱源接觸，桿的側面與外界環境絕熱.現討論該金屬桿的溫度場分布、熱流密度分布及其演化情況，其方程如下

3.2 第二類邊界條件的一維熱傳導問題

長為L均勻鐵制金屬桿，初始時刻桿的左端溫度為0℃，右端溫度為100℃，桿上溫度梯度均勻分布，整個金屬桿與外界絕熱.現討論該金屬桿的溫度場分布、熱流密度分布及其演化情況，其方程如下

其中a=κ/cρ，計算中鐵制桿的密度，比熱容和熱導分別取ρ=7 800 kg/m3,c=500 J/(kg·℃),κ=48.6 W/(m·℃)[1].

3.3 求解的基本方法

問題的求解是基于有限元法[2]，其基本原理是把計算區域劃分成一系列的三角形單元，每個單元上取一個節點，選定一個形狀函數(拋物線型或雙曲線型)，并通過單元中節點上的被求解變量值表示該函數.有限元法的最大優點是對不規則區域的適應性好，故用MATLAB方法求解的結果在邊界上也比較精確[3].

MATLAB中的PDE工具箱在傳熱學中主要用于解如下兩類偏微分方程

式中，u為求解變量，t為時間變量，d，a，f，c為常數或變量.

MATLAB中的PDE工具箱定義了兩類邊界條件，即

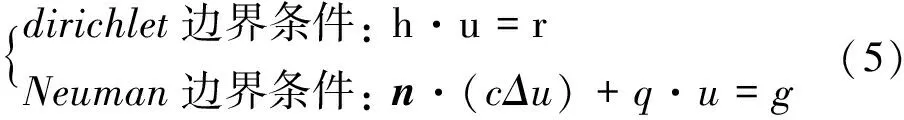
式中n為垂直于邊界的單位矢量，h,r,q和t為常量或與u有關的變量[1，4].

利用PDE工具箱求解導熱問題的一般步驟如圖2所示.

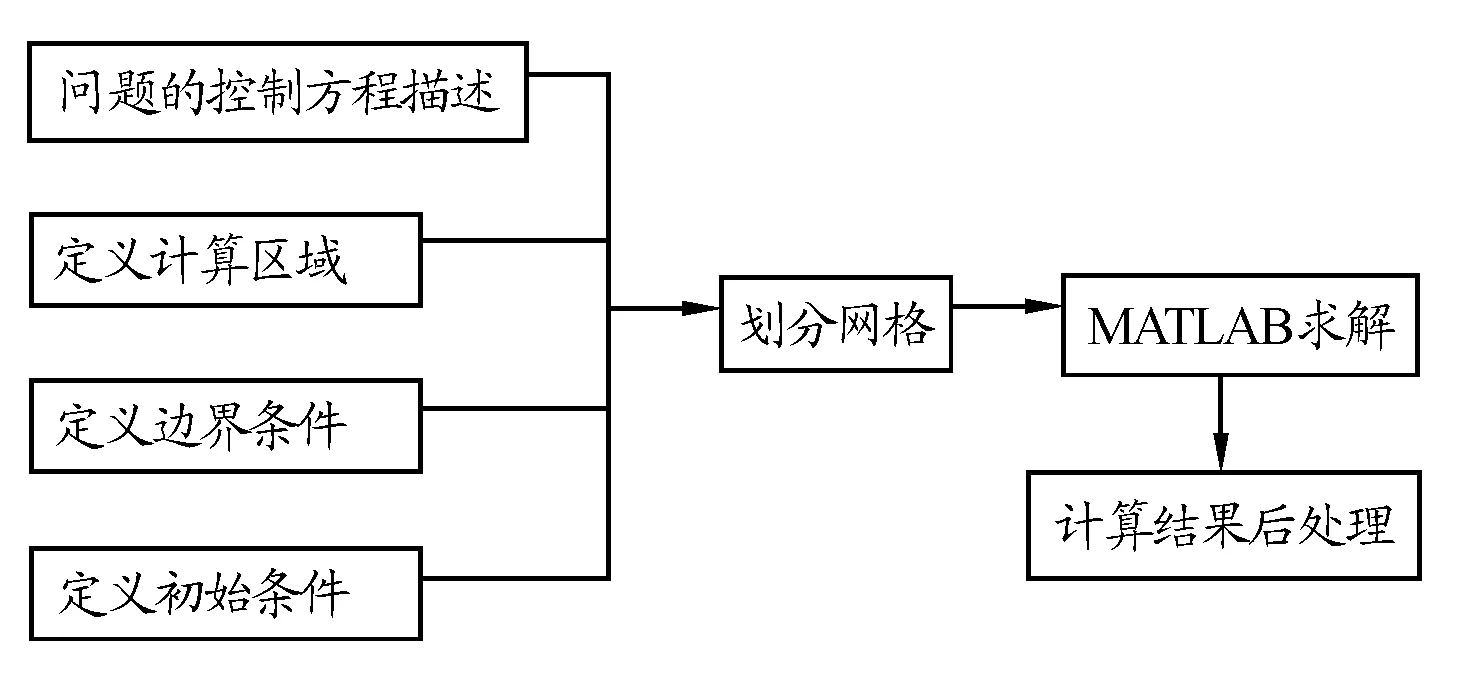
圖2 MATLAB的計算流程圖

4 結果與討論

下面我們用MATLAB中的PDE工具箱來求它們的數值解.

4.1 第一類邊界條件的一維熱傳導問題中的溫度場、熱流密度分布與演化規律

將坐標軸的范圍設為0≤x≤5，-1≤y≤1，求解區域為0≤x≤4,-0.2≤y≤0.2.

矩形的上下邊界為Neuman邊界條件，取q=0，g=0， 左右邊界均為Dirichlet邊界條件， 分別取

h=1，r=0和h=1，r=100.

方程的類型為拋物線類型，其參數分別取c=48.6，a=0，d=7 800×500，f=0，初始條件為u(t0)=20[2].

圖3是經過5小時，20小時，250小時后第一類邊界條件的金屬桿在空間的溫度分布云圖、熱流密度分布云圖，這些圖還顯示了有限元求解的網格.

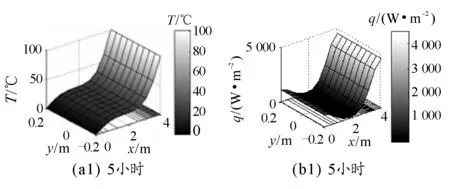
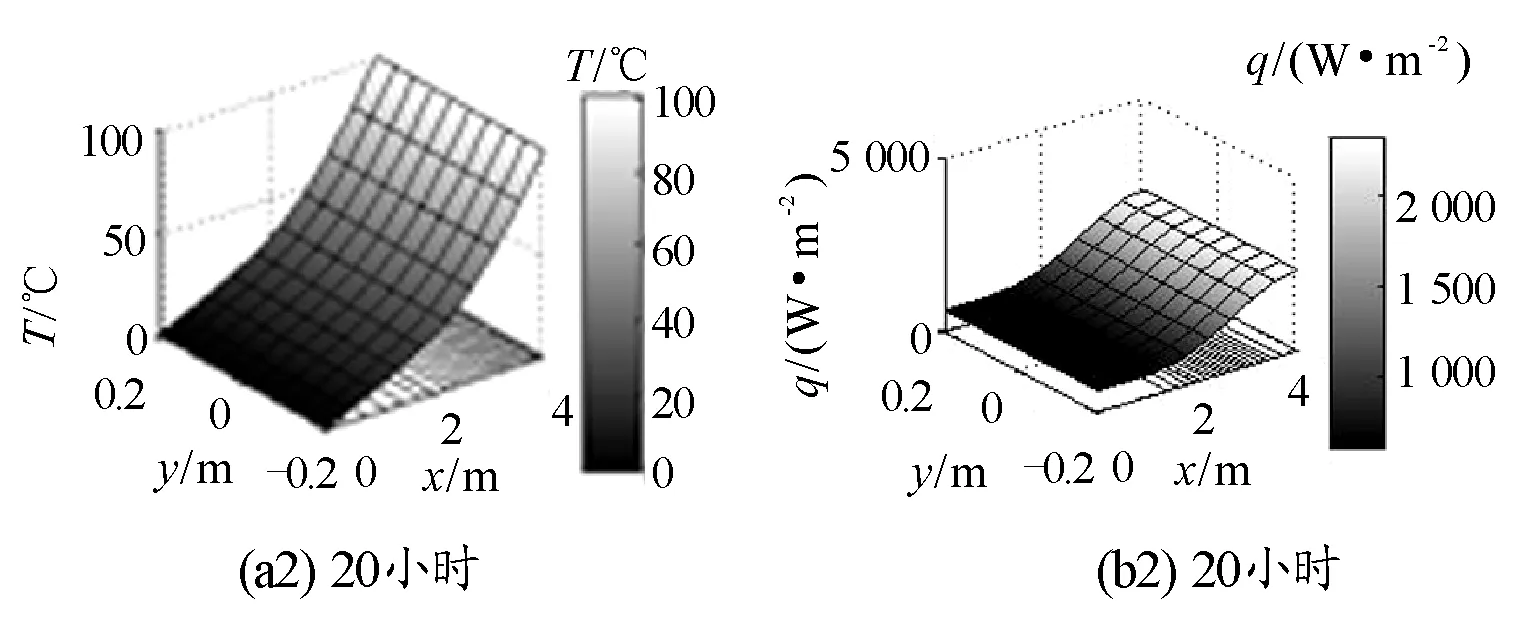
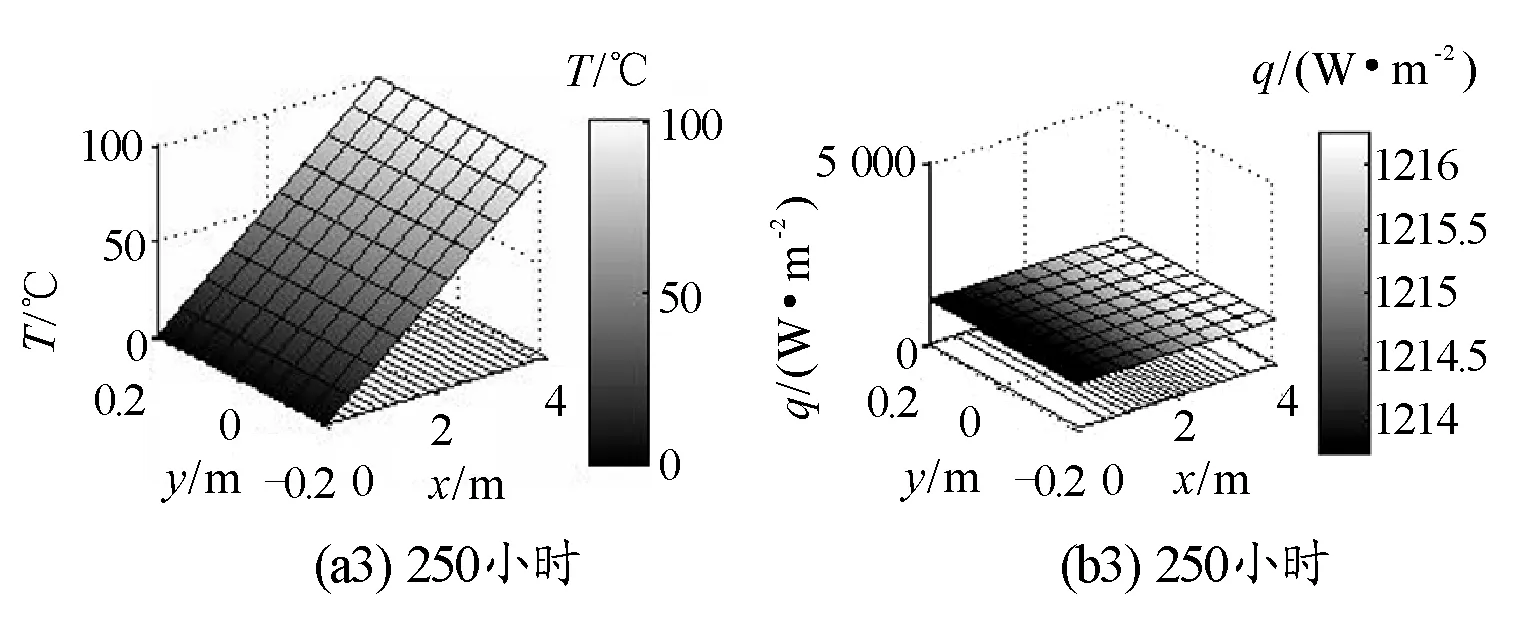
圖3 經過不同時間后第一類邊界條件的金屬桿溫度空間分布云圖及熱流密度分布云圖

由圖3(a1)可知，經過5小時后，金屬桿兩端溫度梯度較大，中間溫度梯度較小.圖3(a2)為，隨著時間的增加，金屬桿不同部位的溫度梯度差異縮小，但溫度分布面仍為曲面；圖3(a3)為，當時間進一步延長，溫度分布面變得平直，說明溫度梯度趨于相等，金屬桿的溫度在空間的分布形成穩定梯度，不同空間位置的溫度分布不再隨時間而發生明顯的變化.

由圖3(b1)可知，經過5小時后，金屬桿不同部位熱流密度的分布是不同的，低溫端熱流密度比較平穩，熱流密度小，而2 m～4 m區域，由于溫度從20℃～100℃變化，熱流密度變化較大，大量的熱由高溫熱源輸運到金屬桿中；圖3(b2)所示，金屬桿不同部位的熱流密度分布存在一定差異，即隨著時間的增加，空間各處熱流密度差異減小；圖3(b3)所示，表明經過足夠長的時間金屬桿各部位的熱流密度趨于相等，對于某一給定區域來說，熱流流入多少，就幾乎流出多少，也就是說，經過足夠長的時間后熱流穩定地從高溫熱源輸運到低溫熱源，這與溫度在空間的穩定分布一致.

4.2 第二類邊界條件的一維熱傳導問題的溫度場、熱流密度分布與演化規律

在使用PDE工具箱求解時，只需將上面求解過程中的左右邊界條件改為Neuman邊界條件，即取g=0，q=0和初始條件設為u(t0)=25×x即可，其余條件不變[2].

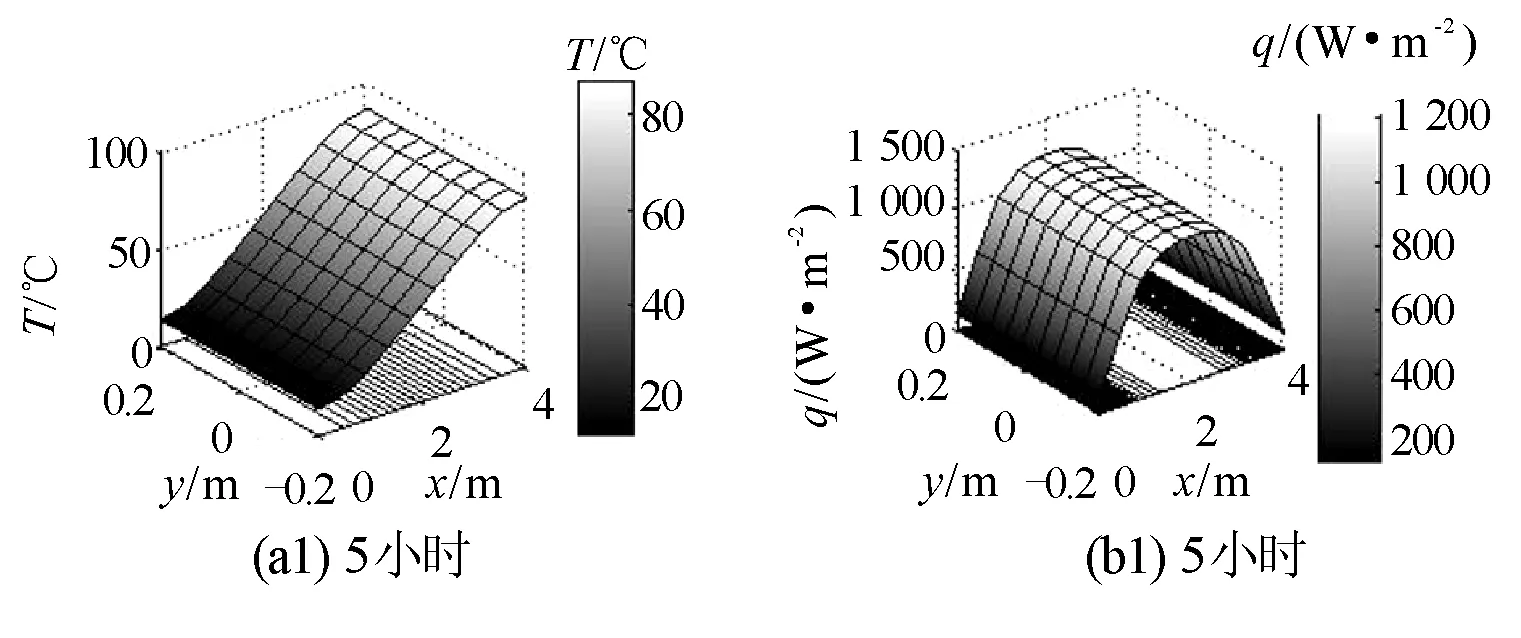
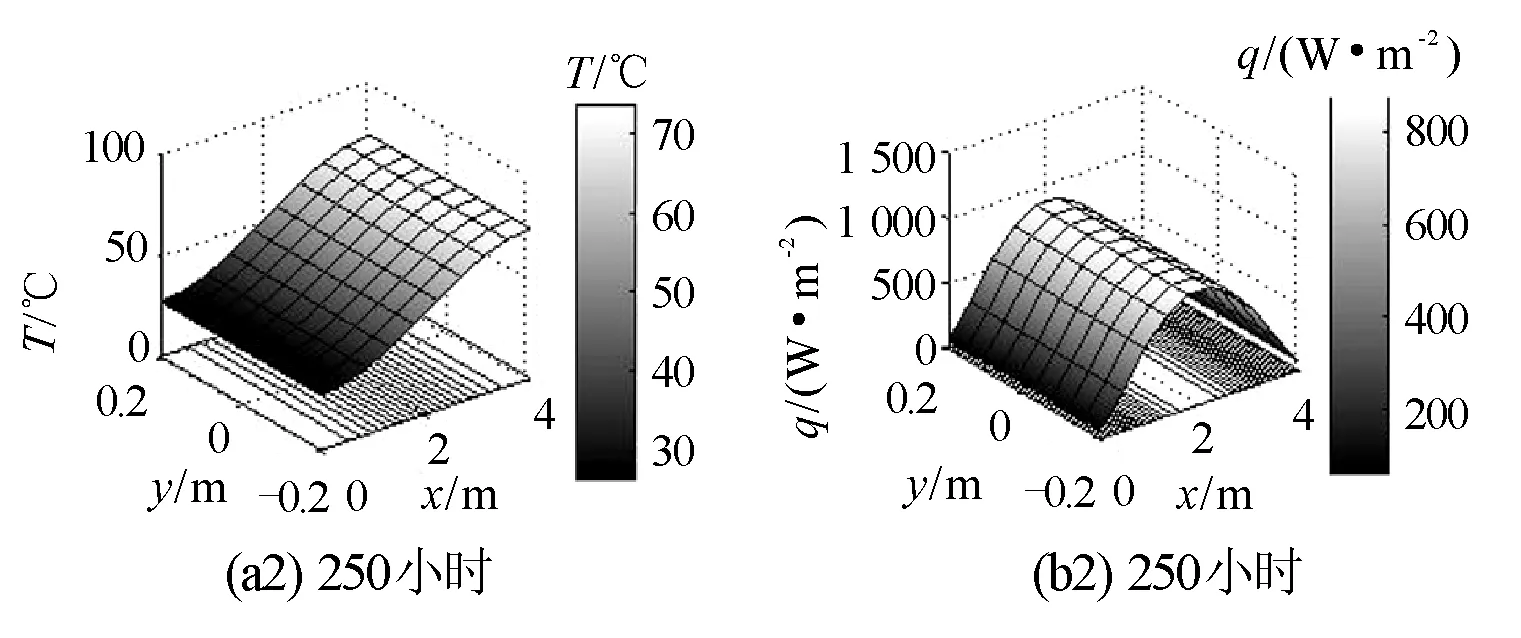
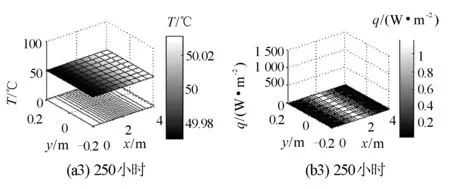
圖4 經過不同時間后第二類邊界條件的金屬桿溫度空間分布云圖及熱流密度分布云圖

圖4是經過5小時，20小時，250小時后第二類邊界條件的金屬桿在空間的溫度分布云圖、熱流密度分布云圖，這些圖還顯示了有限元求解的網格.

由圖4(a1)可知，經過5小時后，金屬桿的溫度分布已發生變化，溫度梯度不再是常量，空間的溫度分布平面變彎曲；圖4(a2)為，隨著時間的增加，斜面變得較平坦，溫度梯度進一步減小；圖4(a3)為，隨著時間的進一步增加，即經過250小時后，溫度分布平面變得幾乎是平行xOy平面，溫度約為50℃，說明金屬桿上各點溫度近似相等，不存在明顯的溫度梯度.即經過足夠長的時間后，金屬桿上的溫度為一個恒定的值50℃.

由圖4(b1)可知，經過5小時后，金屬桿的熱流密度在桿的兩端近似為零，而桿的中間部位的熱流密度相當大并且近似為1 200 W/m2；由圖4(b2)可知，經過20小時后，整個金屬桿中的熱流密度已經大大減小，即隨著時間的增加，金屬桿各部位的熱流密度在減小；由圖4(b3)可知，經過250小時后，金屬桿的熱流密度逐漸趨于零，也就是說，經過足夠長的時間后金屬桿內不存在能量的輸入與輸出，這與溫度在空間的均勻平衡分布是一致的.

5 結論

綜上所述，本文分別對第一類邊界條件下和第二類邊界條件下的金屬桿的一維熱傳導問題進行了可視化分析，從它們的溫度分布云圖和熱流密度云圖可以得出：第一類邊界條件下的金屬桿經過足夠長的時間后，將處在一個宏觀性質不隨時間變化的穩定狀態，即空間各點的溫度是定值，但仍有穩定的熱流從高溫熱源流向低溫熱源，能量在空間各點沒有堆積現象，是一個穩定態.而第二類邊界條件下的金屬桿經過足夠長的時間后，金屬桿上各點的溫度均為50℃，不會隨時間的而變化，而且空間各點的熱流密度也趨于零，是一個平衡態.從二者的比較可知：

(1)有外界影響的情況下，經過足夠長的時間后，金屬桿內空間各點的溫度有穩定分布，但熱流不為零，屬于穩定態.

(2)無外界影響的情況下，經過足夠長的時間后，金屬桿由非平衡態轉化為平衡態，空間各點溫度相等，也無熱流通過.

二者比較更能清楚地區分穩定態與平衡態的區別與聯系，有助于對穩定態和平衡態概念認識的深化.

參考文獻

1 彭芳麟.數學物理方程的MATLAB解法與可視化.北京:北京師范大學出版社,2004

2 陶文銓.數值傳熱學(第2版) .西安:西安交通大學出版社,2001

3 李燦,高彥棟,黃素逸.熱傳導問題的MATLAB計算.華中科技大學學報(自然科學版),2002,30(9):91-93

4 徐梓斌,閔劍青.基于PDE tool的熱傳導數值計算.佳木斯大學學報(自然科學版),2006,24(4):270-272