基于任務規劃的有限推力燃料最優交會①

閆循良,湯一華,徐 敏,陳士櫓

(西北工業大學航天學院,西安 710072)

0 引言

空間交會是實現空間操作和應用的關鍵。航天器往往通過一系列軌道機動實現交會,以完成對接、空間捕獲等任務。要使航天器在各種限制條件下完成不同的空間任務,進行軌道機動任務規劃和軌道優化研究是至關重要的。傳統的軌道機動方式為沖量機動[1-5],它是工程問題的簡單近似。沖量變軌對研究軌道機動仍具有重要意義。在許多情況下,沖量軌道可作為問題的初步模型,而且所得的數值結果可為問題的解決提供重要的參考數據。軌道機動最優需綜合考慮燃料和機動時間。因此,對于沖量變軌必須進行任務規劃,以確定最佳變軌程序。要確定能使總特征速度極小的最優速度變化程序,一般求取解析解是不可行的,必須用計算機來進行分析計算,以確定某個特定飛行任務的適當發射窗口。

實際變軌過程中,推力大小是有限的,推進也不是瞬間的。因此,必須研究有限推力下的變軌問題。目前,研究有限推力交會軌道優化問題的方法主要有間接法和直接法[6-11]。間接法主要應用龐特里亞金極值原理對優化數學模型進行處理,并采用數值方法求解兩點邊值問題,得到最優控制量和相應的軌道。此方法具有較好的求解精度,但需較為準確的、對沒有物理意義的協狀態初值進行猜測。直接法是將軌道優化轉化為參數優化問題,并采用非線性規劃進行數值求解。此方法不需求解兩點邊值問題,收斂半徑大,但求解精度較低,計算量大,控制曲線不光滑。

文中首先以沖量機動作為問題的初步模型,采用Battin-Vaughan算法對雙沖量機動初始位置和飛行時間的組合進行遍歷計算,通過分析和解釋特征速度等值線圖,進行空間交會的任務規劃,為有限推力燃料最優交會提供重要的初值條件。基于任務規劃分析,建立了有限推力燃料最優交會的最優控制模型;采用龐特里亞金極值原理,將最優控制問題轉化為兩點邊值問題,將對伴隨方程的初值猜測轉化為對物理意義明顯的控制量的猜測;采用共軛梯度算法,對兩點邊值問題進行數值求解。在變軌時間固定、連續變推力的情況下,以總沖最小、滿足終端位置和速度約束為指標,對推力大小和方向進行優化。通過仿真對以上算法進行了數值驗證。

1 問題描述

文中研究的問題可描述為追蹤器和目標(或虛擬目標點)分別在兩異面橢圓軌道上運動,在多種限制條件下,追蹤器進行有限推力變軌,并實現與目標點的燃料最優交會,以完成對接或發射有效載荷等任務。

求解有限推力燃料最優交會的關鍵,即尋求最佳飛行軌跡和推力大小、方向隨時間變化的規律,使之滿足交會的各種約束條件,并使燃耗達到最小。為了高效進行有限推力軌道優化,可將沖量機動作為問題的初步模型,通過任務規劃確定變軌初始位置r0、速度矢量v0,交會點位置rf、速度矢量vf,以及變軌時間Δt,進而利用這些重要的初始數據完成有限推力軌道優化。

2 空間交會快速任務規劃

2.1 雙沖量交會描述

假設目標不做機動,若已知轉移時間Δt,根據飛行軌道可計算出目標的末位置及速度矢量,即可得到交會目標點的位置和速度信息。該問題可描述為已知初始時刻追蹤器所在初始點P1的信息r1、v1,目標點P2的信息轉移時間Δt,求解2次沖量Δ使得在Δt時間后,追蹤器與目標點實現交會。可見,該問題實質是高斯問題,可通過解高斯問題得到施加第1次沖量后的速度、施加第2次沖量前的速度以及2次沖量Δ、Δ。

2.2 B-V算法解高斯問題

目前,求解高斯問題的多種方法已建立,除了文獻[3]中的解法以外,還有原始的高斯解法、普適變量法、p迭代法等。以上方法大多需對圓錐曲線類型進行討論,且均無法避免轉移角為π時的奇異性;由Battin等人建立的B-V算法[4]對Gauss算法作出重大改進,計算簡潔,移去了轉移角為的奇異性,并大幅度改善了算法對整個轉移角范圍0～2π的收斂性。

2.2.1 Battin-Vaughan算法

設地心為O,定義弦P1P2長度c=|r2-r1|,三角形OP1P2周長的一半s=(r1+r2+c)/2。經過中值點變換[4]后,設P2點的真近點角為f,偏近點角為E,軌道偏心率為e0,則開普勒方程為

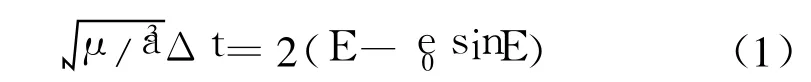
參考高斯代數方程,定義變量:

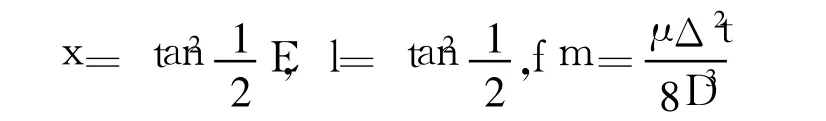
其中,D為連接P1、P2的共軛拋物軌道的中值點半徑:

定義y,滿足

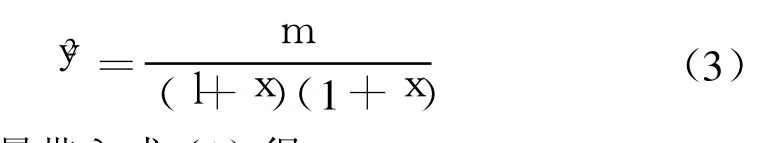
將以上變量帶入式(1),得

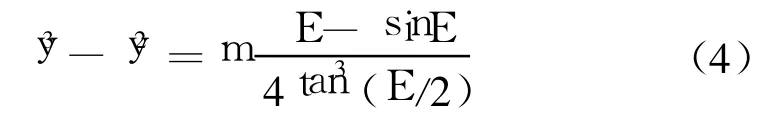
式(3)、式(4)與高斯第一、第二代數方程相似。

引入無量綱參數λ,滿足

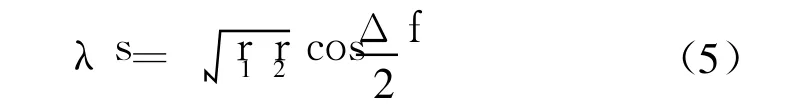
得

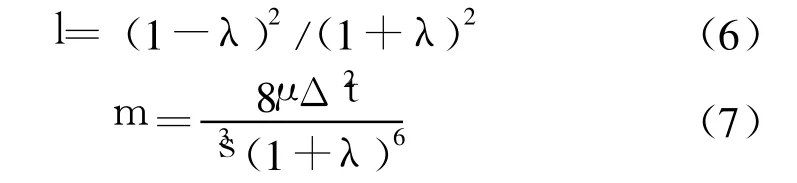
綜上所述,該方法消除了Δf=π處的奇異性。

為了改進求解非線性方程(3)、(4)的逐次代入算法的收斂性,引入h1、h2:

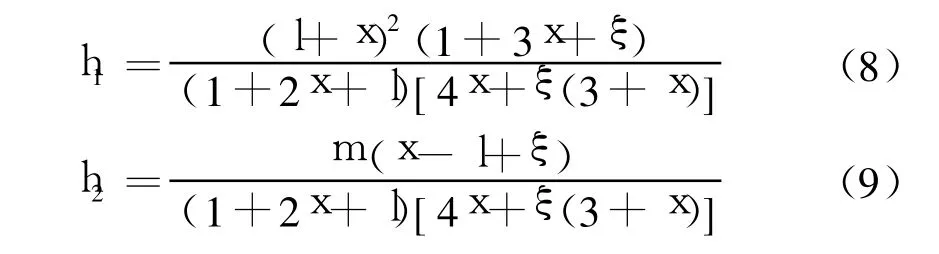
其中

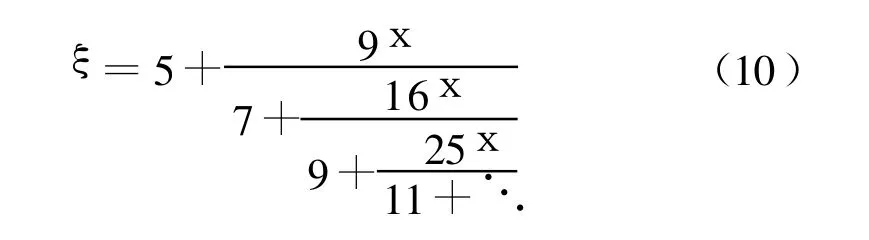
以上方程均適用于各種圓錐曲線。

最終可導出Battin第一和第二代數方程:

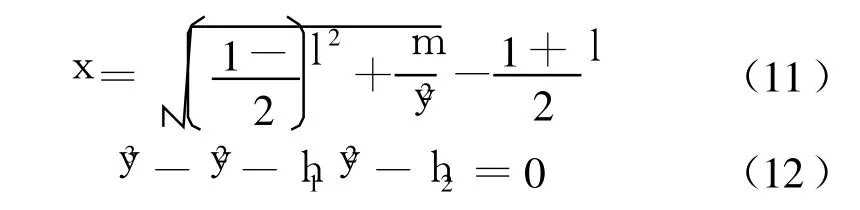
利用B-V算法求解高斯問題的具體步驟參見文獻[4]。

2.3 軌道機動任務規劃

2.3.1 任務規劃分析

追蹤器和目標分別在兩異面橢圓軌道上運動,對于某一雙沖量空間交會,需進行軌道機動任務規劃,以確定追蹤器的最佳初始位置、機動時機、轉移時間及為完成任務所需的特征速度Δv。其中,追蹤器轉移時間和燃料受限。追蹤器在原飛行軌道的初始位置可用當前時刻的真近點角f表示。由于追蹤器初始位置和轉移時間不定,需對初始位置對應的真近點角f和轉移時間Δt的不同組合遍歷求解,進而對結果進行分析。

仿真中,轉移時間限制Δt∈[tmin,tmax],考慮燃料限制,單次沖量大小滿足Δv≤Δvmax,計算步長為t-st;追蹤器初始真近點角f∈[0°,360°],計算步長為f-st。因此,2次沖量大小均可表示為Δ=(f,Δt),Δ=F2(f,Δt),總沖量為

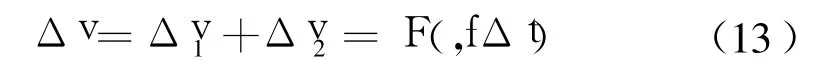
對不同的數據組合(Δt,f),按照2.2節所述方法進行數值求解,得到Δ、ΔΔv,并可作出Δv等值曲線圖,將繪制和分析Δv等值曲線圖作為任務規劃的輔助工具[5]。根據Δv等值線圖,可得到滿足要求的追蹤器初始位置點集(即追蹤區)以及可實現交會的轉移時間范圍。

2.3.2 仿真算例

追蹤航天器初始軌道根數:長半軸a=6 871 km,偏心率e=0.001,軌道傾角i=97.38°,升交點赤經Ψ=60°,近地點幅角ω=20°,真近點角滿足f∈[0°,360°]。目標航天器軌道根數:長半軸=7 171 km,偏心率et=0.01,軌道傾角=100°,升交點赤經Ψt=55°,近地點幅角ωt=30°,真近點角=140°。Δt∈[600 s,5 400 s],t-st=25 s,f-st=1°,追蹤器提供的單次沖量上限Δvmax=3 km/s。

通過數值計算,作出雙沖量交會的Δv等值線圖如圖1所示。

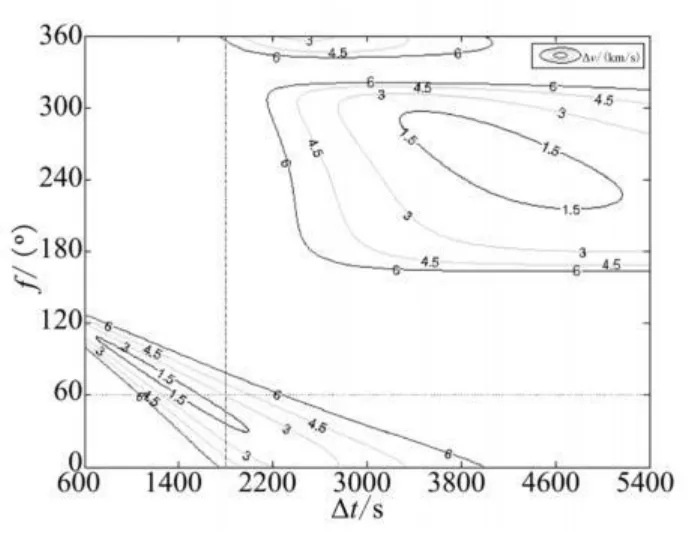
圖1 Δv等值線圖Fig.1 Contour ofΔv

由圖1可直觀地得到滿足燃料限制的(Δt,f)組合范圍,以及滿足燃料、轉移時間限制的f范圍。該f的范圍即對應滿足要求的追蹤器初始位置范圍,或稱之為追蹤區。通過追蹤區即可得到與之對應的發射窗口。對于燃料限制、轉移時間限制和追蹤器初始位置3個量,已知任意2個量的取值,由圖1均可迅速確定第3個量的取值范圍。例如,Δt=1 800 s時,滿足燃料限制的追蹤區為f∈[0°,76°]∪[358°,360°]。同理,若追蹤器初始位置一定,即f給定,亦可得到滿足燃料限制的轉移時間范圍。例如,f=60°時,滿足需求的Δt∈[1 250 s,1 800 s]。

由仿真數據亦可得到任一Δt對應交會問題的燃料最優數值解Δvmin,相應的Δt-Δvmin曲線,以及滿足近似最優解的Δt-f曲線,見圖2。

利用以上數值解及相應的近似解曲線,不需進行繁瑣低效的智能算法尋優,便可確定滿足任意給定初始狀態、燃耗及時間限制的最佳發射窗口,近似最小燃耗,以及燃料最優交會軌道,即可迅速方便進行軌道機動任務規劃。整個計算過程耗時小于10 s。由本節仿真結果可知,在給定的限制條件下,最優的Δvmin≈1.021 km/s,對應的轉移時間Δt≈1 h,追蹤器初始真近點角f≈280°,該組結果為有限推力交會提供了必需的初始條件。

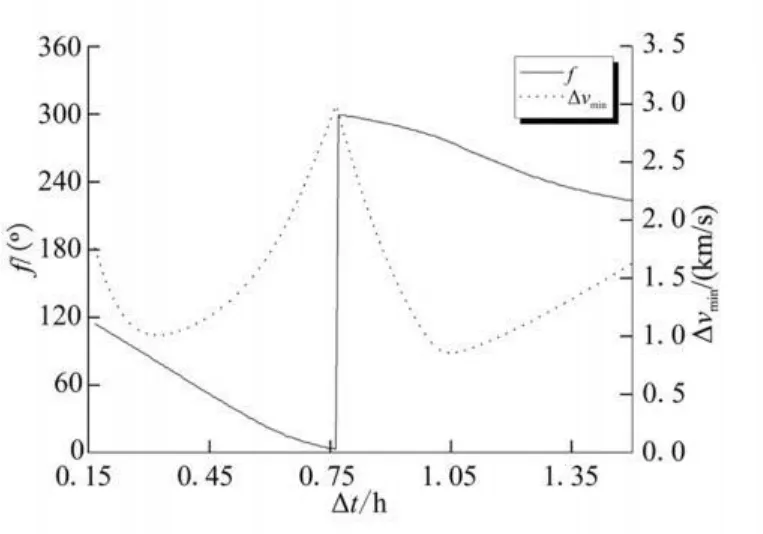
圖2 燃料最優交會f、Δvmin與Δt的關系曲線Fig.2 f vs t andΔv vs tdeterm ined by numerical solutions

3 有限推力燃料最優交會

3.1 動力學模型

考慮地球扁率攝動,在服從平方反比律的中心引力場和有限推力假設下,以相對于地心赤道慣性系的位置、速度為狀態量的變軌運動動力學方程為

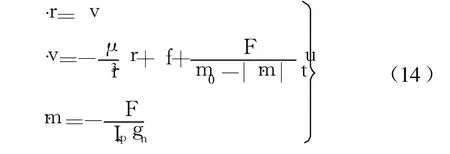
式中 r=[x,y,z]T為航天器地心距矢量;v=[x·,y·,z·]為航天器速度矢量;f為軌道攝動加速度矢量;μ為地球引力常數;F為發動機推力大小;m0為航天器初始質量;|m·|為發動機燃料秒耗量;t為飛行時間;u=[ux,uy,uz]T為推力方向在地心赤道慣性坐標系中的單位矢量;Isp為發動機比沖;gn為標準重力加速度值。

為計算需要,推力方向矢量u可用推力的2個控制方位角α和β表示,即

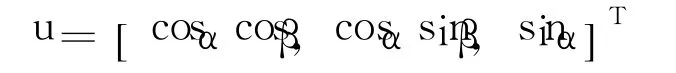
式中 α為俯仰控制角,定義為推力矢量與赤道面的夾角;β為偏航控制角,定義為推力矢量在赤道面的投影與ECI坐標系X軸的夾角。

3.2 最優控制

3.2.1 最優控制數學模型

基于上述的任務規劃,最優控制的目標為尋求最優的控制量α、β、F,使得經過固定時間Δt實現平臺與目標軌道上預定目標點軟交會,且燃料消耗達到最小。

變軌過程發動機推力連續可變,t0和tf為工作起始和終止時間,均可由上述任務規劃獲得。不失一般性,設初始變軌時刻t0=0。交會過程中燃料消耗最少等價于總沖量最小,性能指標為

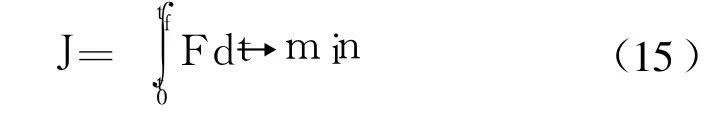
同時,滿足狀態變量邊界約束:

滿足控制變量約束:

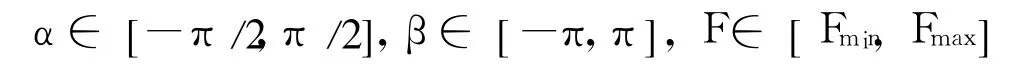
3.2.2 最優控制必要條件

引入哈密爾頓函數:

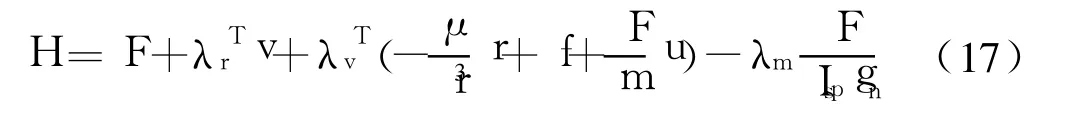
根據極小值原理,最優推力方向應使H達到最小,同時滿足uTu=1,得到

伴隨方程為

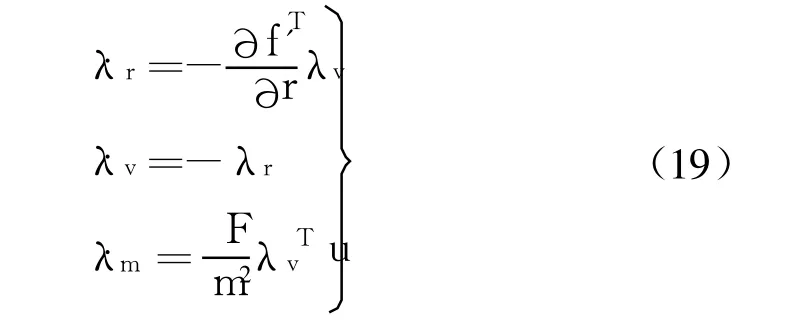
3.3 數值求解

3.3.1 約束處理

對終端條件約束,懲罰函數法(SUMT方法)是較有效的方法之一。由于靜態罰函數適應性較差,懲罰效率不高,利用動態SUMT方法進行約束處理。令X=[x,y,z,x·,y·,z·]T,引入罰函數:

則性能指標變為

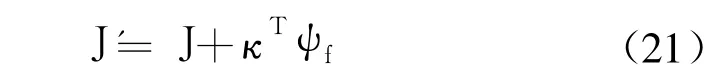
式中 ki為罰因子,其取值原則應使每一個罰函數都與積分項相當。

借鑒模擬退火思想,設計了具有自適應性的退火懲罰函數[10-11]。令ki=1/Ti,其中:

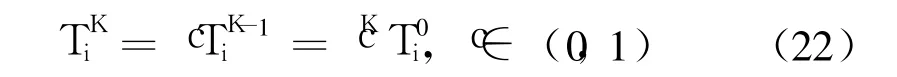
3.3.2 橫截條件

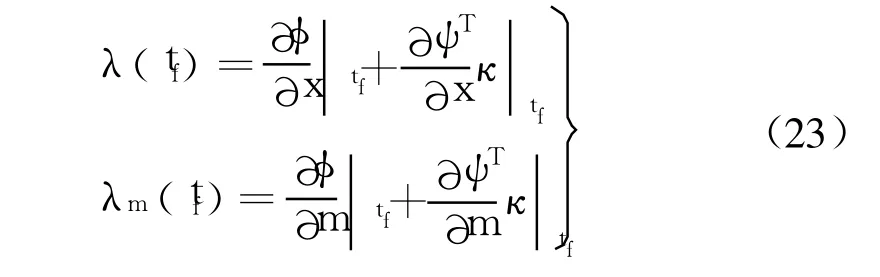
3.3.3 共軛梯度法

共軛梯度法是一種求解最優控制問題的行之有效的方法,通常采用以下公式:

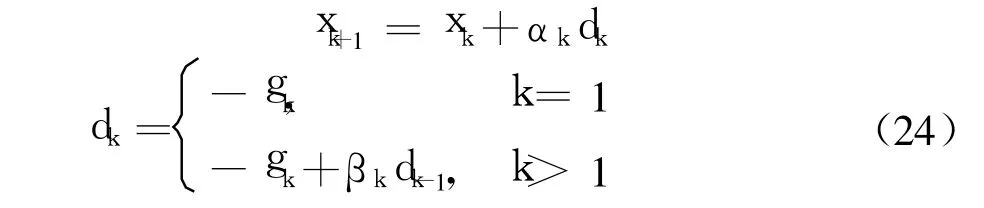
其中,βk為共軛系數,其選取對應了不同的共軛梯度法,PRP方法是目前認為數值表現最好的共軛梯度方法之一,故選取該方法,有=(gk-gk-1,gk)/(gk-1,gk-1),(＊,＊)表示矢量內積。

為了避免對無物理意義的協態量初值進行猜測而引起的初值敏感問題,文中選擇對控制量初值進行猜測,采用共軛梯度法進行求解。具體步驟如下:

(1)在容許控制集中適當猜測初始控制uk。置k=0;設定迭代計算精度ε1、ε2。

(2)用uk和初始條件x(t0)=x0從t0到tf正向積分狀態方程,得到xk。利用橫截條件λ()=λf,從tf到t0反向積分共軛方程,得到λk。

(3)用uk及計算得到的xk和λk計算梯度gk=

如果‖gk≤ε1‖,停止;否則,進行下一步。

(5)用一維精確線性搜索確定最優搜索步長αk＞0,使得

(6)引入控制約束算子

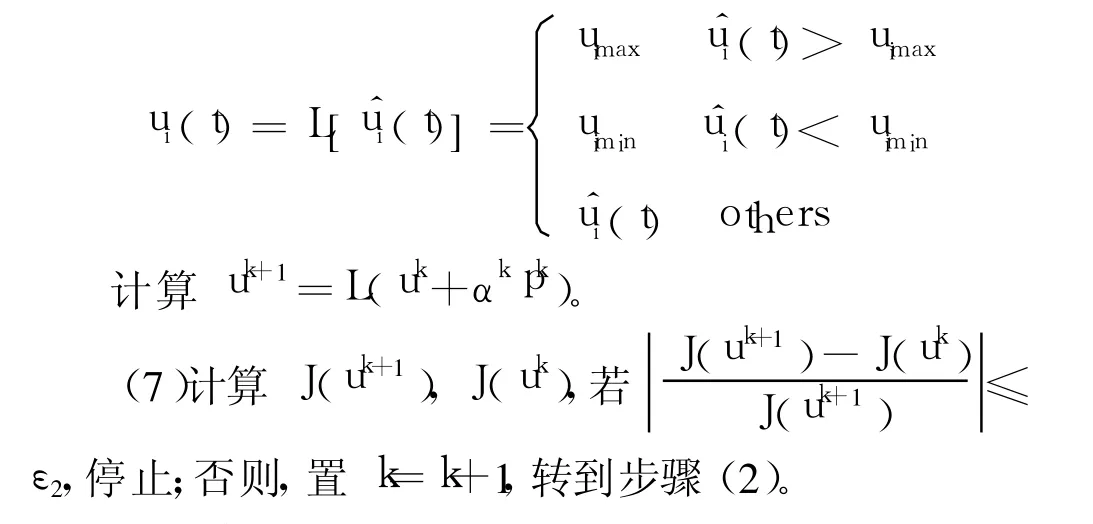
3.4 仿真算例

利用前述任務規劃的數值結果知,追蹤器初始真近點角f=280°,其余軌道根數與2.3.2節相同。追蹤器初始質量為3 000 kg,發動機比沖300 s。交會時間3 600 s,交會精度要求:相對位置±1 km,相對速度±1 m/s。控制量初值選為α=0°,β=0°,F=1 200 N。仿真曲線見圖3～圖6。

由仿真結果可知,滿足交會精度要求時,消耗特征速度1.976 km/s,追蹤器與目標的相對距離為916.4 m,相對速度0.999 8 m/s,在滿足各項限制條件的同時,達到了預設的遠程交會技術指標。有限推力交會消耗的特征速度與雙沖量交會相比,增加了92.9%。主要原因有:

(1)沖量交會假設推力無限大,推力作用是瞬間完成的,而實際的有限推力持續時間較長,存在較大的重力損失。

(2)由于該仿真中,發動機推力較小,將沖量交會時間作為有限推力交會時間,存在一定誤差,進而產生特征速度損失。但將沖量變軌作為初步模型進行空間交會任務規劃,可迅速高效地為有限推力最優變軌提供重要的參考數據,這對注重任務規劃時間的情況(如空間打擊)而言,具有積極而重要的意義。

同時,文中采用的數值求解技術,降低了初值猜測難度,提高了求解兩點邊值問題的效率,所得最優解平滑,精度較高。但由于間接法求解最優化問題的固有特性,文中方法仍無法完全避免初值敏感問題。

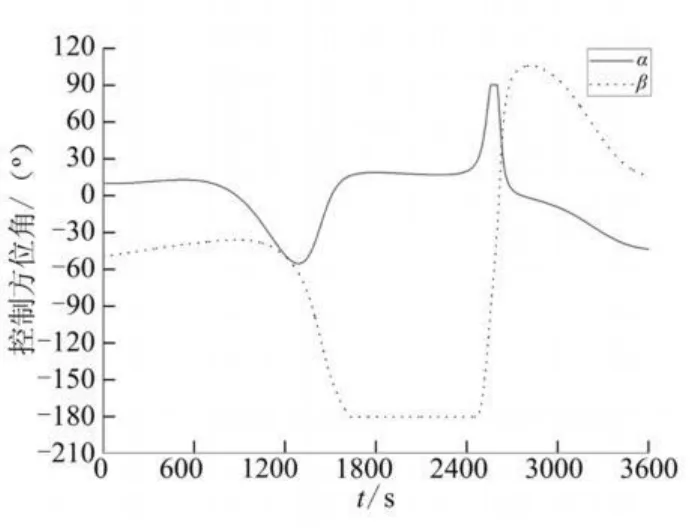
圖3 推力方向變化曲線Fig.3 Curves of thrust direction vs time

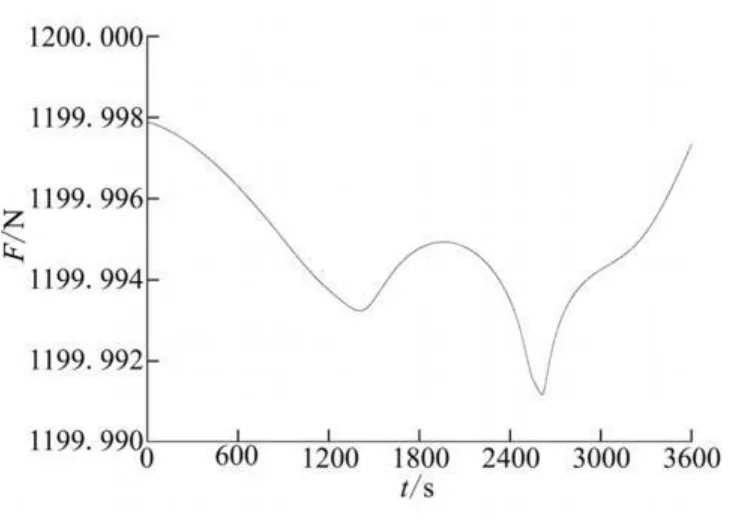
圖4 推力大小變化曲線Fig.4 Curves of thrustm agnitude vs time

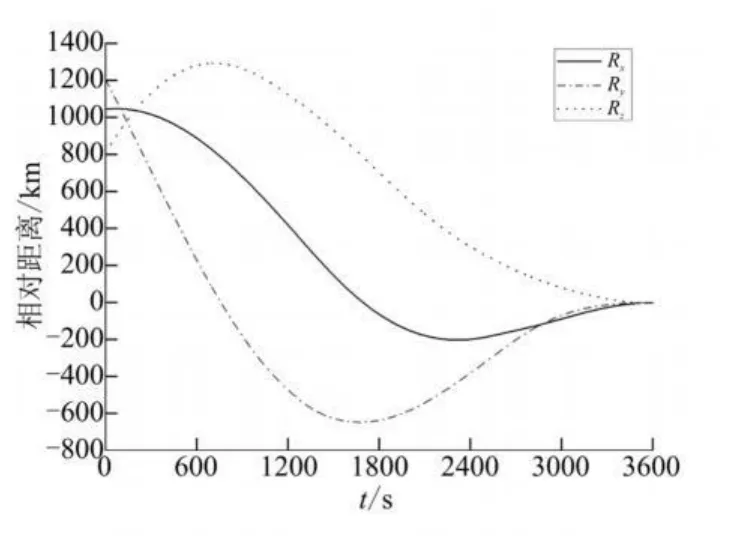
圖5 相對距離變化曲線Fig.5 Curves of relative distance vs time

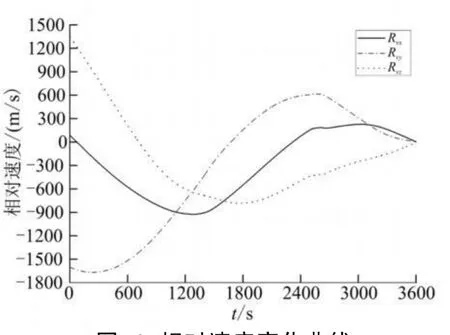
圖6 相對速度變化曲線Fig.6 Curves of relative velocity vs time

4 結論

(1)采用B-V算法求解高斯問題,不需對圓錐曲線類型進行討論,計算簡潔,移去了轉移角為π的奇異性,并大幅度改善了算法對整個轉移角范圍的收斂性。

(2)對空間交會等任務分析而言,將繪制和分析等值線圖作為任務規劃的輔助工具,是普遍適用和有效的,能直觀快速地為工程應用提供參考。

(3)將沖量變軌作為初步模型進行空間交會任務規劃,可迅速高效地為有限推力最優變軌提供重要的參考數據。

(4)將有限推力交會最優控制伴隨變量初值猜測轉化為對物理意義明顯的控制量初值的猜測,極大地降低了求解兩點邊值問題的難度,所得最優解平滑,精度較高,可作為工程應用的相關參考。

[1] Prussing JE,Chiu JH.Optimal multiple-impu lsetime-fixed rendezvous between circu lar orbits[R].AIAA-84-2036.

[2] 張立佳,郭繼峰,崔乃剛.伴飛航天器燃料最優交會[J].宇航學報,2007,28(4):870-874.

[3] 陳統,徐世杰.基于遺傳算法的最優Lambert雙脈沖轉移[J].北京航空航天大學學報,2007,33(3):273-277.

[4] Richard H Battin,Robin M Vaughan.An elegant lambertalgorithm[J].J.guidance,7(6):662-670.

[5] Haijun Shen,Panagiotis Tsiotras.Optimal two-impulse rendezvous using multip le-revolution lambert solutions[J].Journalof Guidance,Control and Dynamics,2003,26(1):50-61.

[6] John TBetts.Survey of numerical methods for trajectory optimization[J].Journal of Guidance,Control and Dynamics,1998,21(2):193-207.

[7] Gao Y,Kluever C A.Low-thrust interplanetary orbit transfers using hybrid trajectory optimization method with multiple shooting[R].AIAA 2004-5088.

[8] Paul J Enright,Brace A Conwayt.Optimal finite-thrust spacecraft trajectories using collocation and non linear programming[J].J.Guidance,1991,14(5):981-985.

[9] Yuri Ulybyshev.Continuous thrustorbit transfer optimization using large-scale linear programming[J].Journal of Guidance,Control and Dynamics,2007,30(2):427-436.

[10] 朱建豐,徐世杰.基于自適應模擬退火遺傳算法的月球軟著陸軌道優化[J].航空學報,2007,28(4):806-812.

[11] 任遠,崔平遠,欒恩杰.基于退火遺傳算法的小推力軌道優化問題研究[J].宇航學報,2007,28(1):162-166.