基于Copula模型的降雨量與土壤飽和度的模擬研究*

王沁，黃雁勇，湯家法，向波

(1.西南交通大學數學學院，四川成都610031;2.西南交通大學土木工程學院，四川成都610031)

對一次泥石流而言，前期有效降水量和當次有效降水量共同決定了泥石流的形成［1］，是泥石流預報的重要參數。前期降水的有效部分以土壤水的形式積累在土壤中，所以，流域的土壤飽和度狀況，是形成泥石流的關鍵性水文因素之一。了解土壤飽和度的變化狀況，對于泥石流預報中的前期降水條件評估以及理解泥石流的觸發水文條件等方面都有重要的科學意義。

Copula連接函數是一種靈活、穩健的相關性分析的工具，它將邊緣分布及相關性結構分開處理，度量了變量之間的相關程度和相依模式，與面向均值、方差和線性相關的建模方法不同，對整個聯合分布建模提供更多有用信息，在金融領域［2－4］、水文領域［5－9］、概率地震危險性［10］分析等方面得到廣泛應用。

Zhang L應用Copula函數對靜態與非靜態的洪水、降雨和枯水進行了兩變量及三變量的頻率分析［5］，并用Copula函數擬合河道中流速和水深的聯合分布，還進行了水質的多變量分析;Salvadori和De Michele［9］基于Copula函數進一步研究了暴雨統計量的聯合分布，進而推導出暴雨前某固定時段內降雨量和前期土壤飽和度的分布函數。

本文以云南東川蔣家溝為研究對象，以一個基于小流域水分循環的基本物理過程所開發的土壤飽和度模擬模型為基礎［11－12］，獲得了流域內的土壤飽和度與降水量兩個變量的數據。基于土壤飽和度與降水量的樣本數據，采用皮爾遜Ⅲ型分布擬合土壤飽和度與降雨量，選用能夠較好反映降雨和土壤飽和度之間相關結構的Clayton Copula函數，建立兩變量聯合分布，分析兩變量重現期，模擬了流域內土壤飽和度的變化情況。

1 Copula連接函數與Clayton Copula函數

假設隨機變量(X1，X2)的聯合分布為H(x1，x2)，邊緣分布函數分別為Fi(xi)=P(Xi≤xi)，那么，存在唯一的連接函數Copula函數C(·)使得［13］:

式中:ui=Fi(xi)=P(Xi≤xi)是邊緣分布函數，Ui=F(Xi)服從標準均勻分布。

設(X1，Y1)，(X2，Y2)為相互獨立，聯合分布為H(x1，x2)的二維隨機變量，則連接函數Copula的Kendall的秩相關系數為［13］:

Kendall的秩相關系數刻畫了兩個變量變化趨勢是否一致。如果Kendall的秩相關系數為正值，說明兩個變量變化趨勢是正相關的，一個變量變大，另一個變量變大的趨勢大;如果Kendall的秩相關系數為負值，說明兩個變量變化趨勢是負相關的，一個變量變大，另一個變量變小的可能性大。

Clayton Copula函數族，其連接函數為［13］:

其Kendall的τ為:

運用Copula連接函數構建模型，常采用兩步法。第一步，利用某類分布或時間序列分析方法確定邊緣分布;第二步，定義一個適當的連接函數Copula，以便能很好地描述出邊緣分布的相依結構、相互耦合作用。由此看出，運用連接函數Copula描述多變量之間相互耦合時，可以將邊緣分布和相關結構分開來研究，這有助于對很多變量的相互耦合作用進行分析和理解。

2 基本資料和邊緣分布分析

流域水文條件變化是一個復雜的過程，降水通常是整個過程的開始，經過截留、滲透、蒸發等若干環節，最終改變土壤飽和狀況。由于土壤飽和度的數據難以直接獲得，文獻［11－12］中，采用了一個基于水分循環物理過程的分布式水文分布模型獲得了蔣家溝流域的不同降雨量下土壤飽和度逐日變化的數據［11］，數據分布如圖1所示，這也是本文分析所使用的數據。

圖1 蔣家溝流域的不同降雨量下土壤飽和度的變化趨勢圖

從圖1可以看出，流域的土壤平均飽和度從雨季開始呈上升趨勢，一直到7月中下旬開始達到一個比較高的數值，一直到8月底都維持在較高的水平之上，但隨著降水的變動而劇烈變化，到9月份隨著降水的減少逐漸降低，最后穩定在一個較低的水平。所以，降水與流域的土壤平均飽和度二者存在著緊密的關系，但這種關系并不是簡單的增加過程，而是復雜的非線性過程。

在水文分析計算，常采對數正態分布、指數分布、Gumbel分布及皮爾遜Ⅲ型分布等來分析洪峰、洪量等變量。本文采用均值參數為零的皮爾遜Ⅲ型(即三參數Gamma分布)分析土壤飽和度。參數估計的結果為:偏態系數(s)為1.005 2，變差系數為66.710 4，其QQ圖如圖2所示。

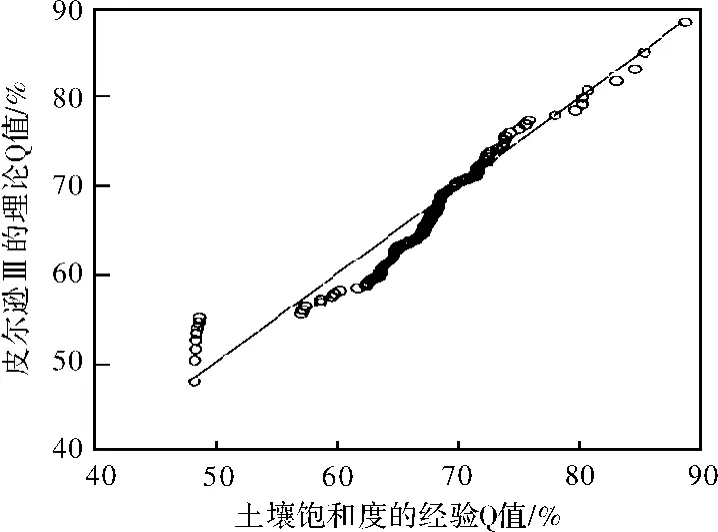
圖2 皮爾遜Ⅲ型與土壤飽和度的QQ圖

圖2說明了利用偏態系數(s)為1.005 2，變差系數為66.710 4的均值參數為零的皮爾遜Ⅲ型能較好擬合土壤飽和度。

采用均值參數為零的皮爾遜Ⅲ型(即三參數Gamma分布)來分析雨量，其相應結果如表1所示。其累積分布圖如圖3所示。

表1 皮爾遜Ⅲ型分析雨量的相應結果

圖3 皮爾遜Ⅲ型與雨量的累積分布函數比較

K－S擬合優度檢驗方法的相伴概率和累積分布圖都說明了，利用均值參數為零的皮爾遜Ⅲ型分布來分析雨量是比較恰當的。

3 聯合分布函數

根據飽和度和雨量的資料，首先求得樣本Kendall的秩相關系數，即:

利用土壤飽和度與雨量的樣本數據求出Clayton連接函數的參數為:

為了檢驗Clayton連接函數連接土壤飽和度與雨量的擬合精度，比較經驗連接函數與理論連接函數的累積概率。

假定(X1，Y1)，(X2，Y2)，…，(Xn，Yn)來自飽和度與雨量的聯合分布H(x，y)，設U=F(x)，V=G(y)是均勻分布，則:

則M(ω)的經驗估計為:

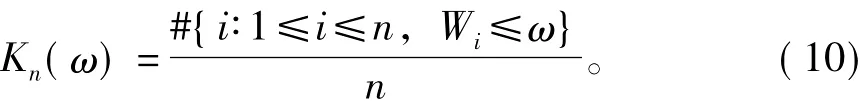
而其理論估計為:

采用無抗舍養、無抗放養、有抗舍養和有抗放養等方式進行固始雞養殖，測定不同養殖階段雞腿肉、胸肉和肝臟中氨基酸及其組成，以研究不同養殖方法對其雞肉品質的影響。結果表明，在舍養條件下有抗養殖與無抗養殖比較，隨著養殖時間的延長，無抗養殖在雞胸肉和腿肉中總氨基酸略高于有抗養殖，而呈鮮味和必需氨基酸有抗養殖略高；放養條件下有抗養殖與無抗養殖比較，總氨基酸、呈鮮味氨基酸、必需和非必需氨基酸，無抗養殖均略高。

式中:φ為阿基米德連接函數的生成元。分別計算M(ω)的經驗估計與理論估計，從而畫出PP圖(圖4)。

圖4說明了利用Clayton連接函數來分析土壤飽和度與雨量之間的相依關系是比較恰當的。

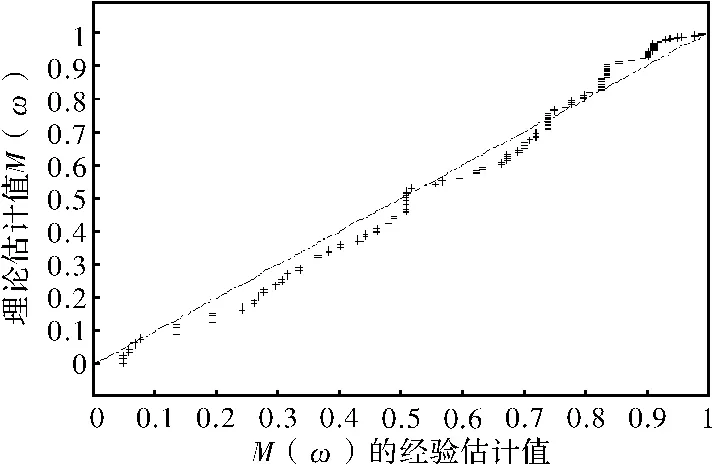
圖4 M(ω)的經驗值與M(ω)的理論值的PP圖

表2 Clayton連接函數的擬合優度檢驗結果

從擬合優度檢驗的結果可以看出，利用Clayton連接函數能細致刻畫了雨量與土壤飽和度之間的相依關系，能捕捉雨量與土壤飽和度之間的相依機制。

4 聯合重現期和隨機模擬

定義變量飽和度X和雨量Y的聯合重現期:

定義另一種聯合重現期:

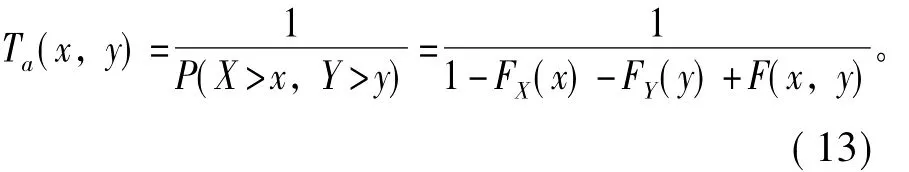
分別計算不同頻率p下所對應的閥值xp，yp，然后根據Clayton連接函數計算(xp，yp)的聯合重現期To(xp，yp)、Ta(xp，yp)，相應結果見表3。

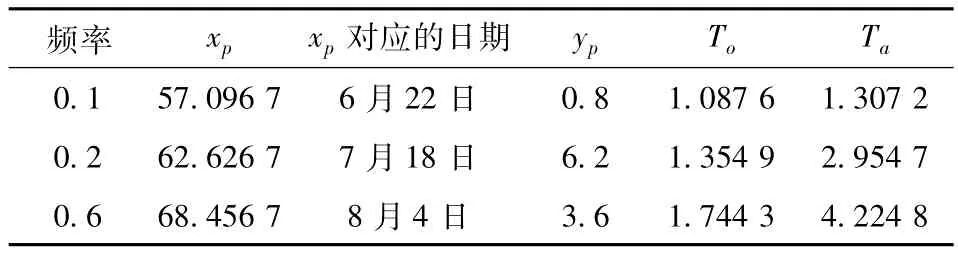
表3 聯合重現期To(xp，yp)與Ta(xp，yp)

從表3的計算計算結果以及xp對應的日期，可知To(x0.2，y0.2)≈15個月，Ta(x0.2，y0.2)≈32個月，即在7月18日后發生土壤飽和度X>57.096 7或雨量Y>0.8的聯合重現期是15個月左右;發生土壤飽和度X>57.096 7同時雨量Y>0.8的聯合重現期是32個月左右。在7月18日后經歷了15個月和32個月后的時段內可能是蔣家溝泥石流的高發時段。

由于在實際中，飽和度的數據較難得到。所以，可以通過相應Clayton連接函數來模擬產生飽和度的數據。隨機模擬的步驟如下:

(1)令V=G(y)，其中G是雨量的分布函數，即表2中的皮爾遜Ⅲ型分布;

(2)產生服從標準均勻分布的隨機變量W，即W服從［0，1］上均勻分布;

(4)令BHD=F－1(U)，其中F－1為飽和度分布函數的逆函數，即表1中的皮爾遜Ⅲ型分布的逆函數。

利用Clayton連接函數做隨機模擬，得到飽和度的模擬數據，其相應結果如圖5所示。

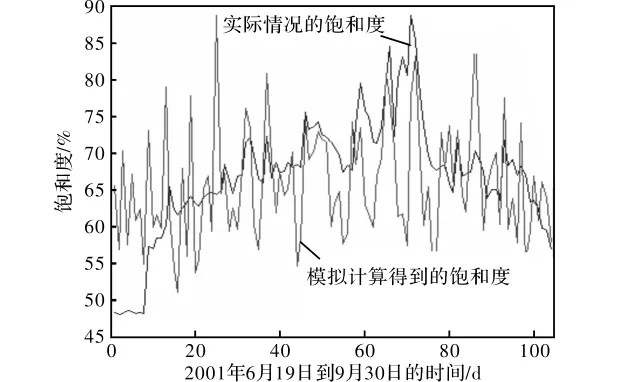
圖5 模擬產生的飽和度數據與實際飽和度的比較圖

為了檢驗模擬產生的結果好不好，采用平均偏差與均方誤差作為評價指標。平均偏差Bias與均方誤差Rmse的計算結果如下:

式中:Xi，分別為估計值和真實值。

從平均偏差Bias與均方誤差Rmse的結果可以看出，利用Clayton連接函數做隨機模擬法產生的飽和度數據能夠較真實地反映實際的飽和度。

5 小結

本文利用皮爾遜Ⅲ型分布分別對土壤飽和度與雨量進行了擬合，選用能夠較好反映土壤飽和度與雨量之間的Clayton連接函數，建立了兩變量聯合分布。其主要結論如下:

(1)擬合優度指標表明皮爾遜Ⅲ型分布能較好地擬合土壤飽和度與雨量。

(2)經驗連接函數與理論連接函數的PP圖，以及K－S檢驗方法都表明土壤飽和度與雨量之間的相依機制為Clayton連接函數。

(3)從Clayton連接函數出發，獲得飽和度和雨量的各種組合的聯合重現期，為預測泥石流的發生提供了一種新方法。

(4)從Clayton連接函數出發，隨機模擬了飽和度，為某些尚不能測量飽和度的地區提供一種根據雨量預測土壤飽和度的變化的新方法。

［1］韋方強，胡凱衡，陳杰.泥石流預報中前期有效降水量的確定［J］.山地學報，2005，23(4):453－457.

［2］Patton AJ.Modeling time－varying exchange rate dependence using the conditional copula［C］//Working Paper of Department of Economics.San Diego:University of California，2001.

［3］Patton AJ.Estimation of copula models for time series of possibly different lengths［C］//Working Paper of Department of Economics.San Diego:University of California，2001.

［4］Rodriguez J C.Measuring financial contagion:a copula approach［C］//Working Paper of European Institute for Statistics Probability，Operation Research and their Applications，Eurandom，2003.

［5］Zhang L.Multivariate hydrological frequency analysis and risk mapping［D］.Louisiana:Louisiana State University，2005.

［6］Salvatore G，Francesco S.Asymmetric copula in multivariate flood frequency analysis［J］.Advances in Water Resources，2006，29:1155－1167.

［7］肖義.基于Copula函數的多變量水文分析計算研究［D］.武漢:武漢大學，2007.

［8］肖義，郭生練，熊立華，等.一種新的洪水過程隨機模擬方法研究［J］.四川大學學報:工學版，2007，39(2):55－60.

［9］Salvadori G，De Michele C.Statistical characterization of temporal structure of storms［J］.Advances in Water Resources，2006，29(6):827－842.

［10］李彥恒，史保平，張健.聯結(Copula)函數在概率地震危險性分析中的應用［J］.地震學報，2008，30(3):292－301.

［11］湯家法.蔣家溝流域土壤濕度變化模擬研究［J］.山地學報，2009，27(2):217－222.

［12］湯家法.蔣家溝泥石流激發土壤水分條件的模擬與分析［J］.地質災害與環境保護，2009，20(3):90－95.

［13］Roger B′Neslen.An introduction to copulas［M］.New York:Springer Verlag，1999.