旱地生態(tài)學(xué)問題弱解的估計
吳軍優(yōu),李若霞,臧 慧,王艷明
(黃淮學(xué)院 數(shù)學(xué)科學(xué)系,河南 駐馬店 463000)
在旱地生態(tài)學(xué)問題的研究中,生態(tài)學(xué)家在[1]中提出了如下微分方程的生態(tài)學(xué)模型:

Ω奐R2,Ω為具有光滑邊界的區(qū)域,β,γ,σ,μ,δ,ρ,p均為正常數(shù),n表示植物量密度,w表示地下水的密度,源項p表示降雨量。通過對該模型建立解的正則性估計,能夠使生態(tài)學(xué)家給沙漠化現(xiàn)象以理論解釋。這里我們對n,w在x,y方向分別提周期邊界條件。
下面用Ci(i=1~23)表示各種不同的正常數(shù)
定理:(弱解的正則性)設(shè)n0,w0∈H2(Ω)則對系統(tǒng)(1.1)-(1.3)的非負(fù)弱解有:
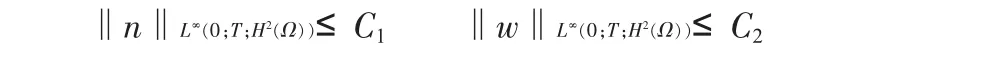
其中C1,C2是僅與β,γ,σ,μ,δ,ρ,p,T及初值有關(guān)的常數(shù)。
證明:對方程(1.1)運(yùn)用極值原理及能量方法有:
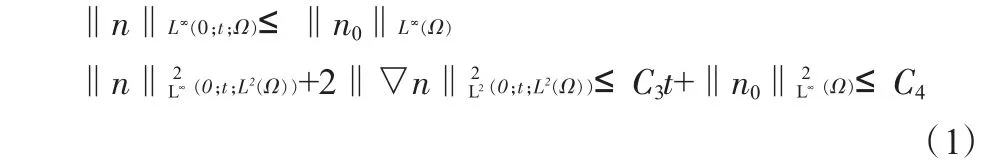
對方程(1.2)運(yùn)用能量方法及Gronwall不等式有:
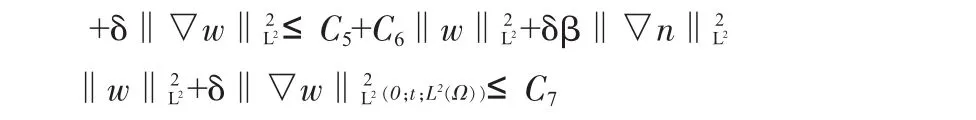
對方程(1.1)關(guān)于t求導(dǎo)并運(yùn)用能量方法有:
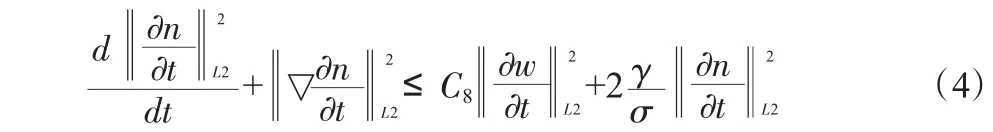
對(1.2)關(guān)于t求導(dǎo)并運(yùn)用能量方法及Sobolev不等式有:
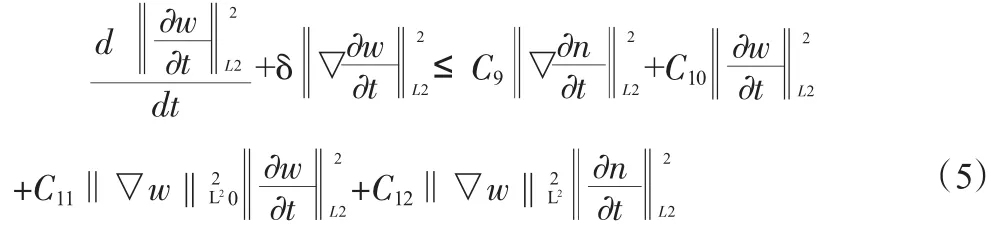
由(4)、(5)兩式Gronwall不等式得:

由方程(1.1)(1.2)得:
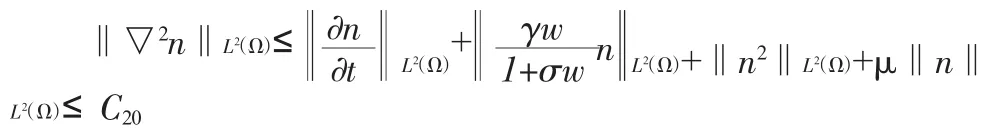
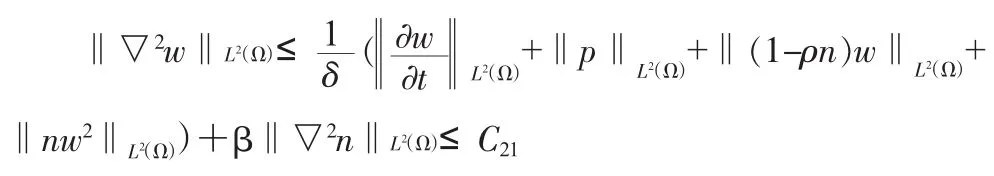
由Stokes方程正則性結(jié)果得:
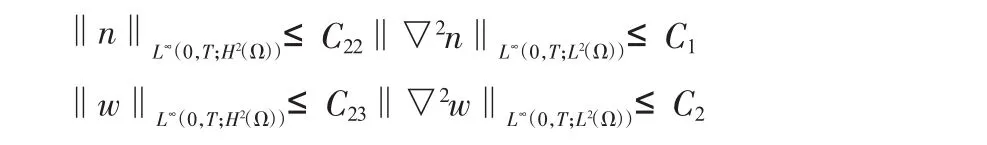
定理即證。
[1]J.von Hardenberg,E.Meron,M.Shachak,etc.,Diversity of Vegetation Patterns and Desertification[J].Physical Review letters,2001,87(19).
[2]R.lefever,O.lejeune,P.couteron,In mathematical models for biological pattern[J].IMA,2000,121(2):83~112.

