空間二次曲線射影重建計算方法研究

張政武

（陜西理工學院機械工程學院，陜西 漢中 723003）

計算機視覺的基本目的之一就是通過分析景物的一幅或多幅圖像來揭示景物的本質特征。由于在投影過程中，三維景物的空間關系、物理性質以及表面的物理特性在二維圖像中綜合為圖像點的灰度值，因此，在得到二維圖像的過程中丟失了景物的深度信息，正是由于要恢復這種丟失的深度信息便組成了計算機視覺研究的核心問題——從景物圖像或序列圖像恢復三維景物的形狀、位置、運動等物理特征。

將二次曲線作為一個重要的基本要素來實現對三維場景的理解和識別是計算機視覺研究的一個重要的領域。近幾年來，研究人員在這方面做了大量的工作，在圍繞著二次曲線計算方法的研究方面取得了不少的成績[1-6]。文獻[1]通過對多幅圖像中二次曲線上多個點的檢測來求解二次曲線；文獻[2]中通過對二次曲線上不同直線的檢測來實現對二次曲線的恢復；文獻[3]利用幾何代數來表示二次曲線，通過求解兩個不同點上線束的對應直線交點推導出二次曲線的幾何積的表達形式；文獻[4]、[5]是將一條二次曲線表示為P5射影空間中的一個點或者一個稱為二次曲線矢量的六維矢量，然后通過一個6×6的射影變換矩陣推導出了從一個給定的二次曲線基變換為點基的線性算法和兩幅圖像對應的約束條件，實現了對物體的識別；文獻[6]提出一種二次曲線的整體表示法，即給出了空間二次曲線和平面二次曲線的坐標表示法，該坐標是由不全為零的9個數構成的有序數組，建立了基于動態灰度圖像和基于序列灰度圖像的二次曲線光流的概念。上述方法,總的來說是利用點、直線坐標或是利用矢量運算來對二次曲線進行檢測和識別，在實際情況中，由于圖像數據存在噪聲，通常需要利用迭代法以求解多元方程組的最優解，這就存在迭代法不收斂或收斂到一個局部而非全局的最優解的可能性。本文從實際計算的角度出發，將一條二次曲線表示成一個空間錐面和一個平面的交線，利用兩個二次曲面的基曲線推導出二次曲線重建的對應條件，在此基礎上，給出了空間二次曲線射影重建的計算方法，最后通過實驗驗證表明該算法實用、可靠。

1 空間二次曲線的射影重建

1.1 空間二次曲線

射影空間中點和平面互為對偶，因此平面二次曲線的空間對偶就是錐面，同時二次曲線是一 個秩為3的二次包絡[7]。設錐面為T0=x Qx （Q是 4× 4的對稱矩陣），空間平面為π = pTx =0， 當用平面坐標代替點坐標時，二次曲線的平面方程能夠表示成一個空間錐面和一個平面的交線

其中 平面 u=( u1, u2, u3,u4)T是變平面。

1.2 空間二次曲線的射影重建

設雙目立體視覺中兩個攝像機的投影矩陣分別為P 和P′，射影重建是指確定這對射影矩陣P 和P′之間的射影變換，因此就要在射影空間中研究二次曲線重建的內部特征。

假設給定兩幅圖像中的一對對應二次曲線

對空間二次曲線進行射影重建就是要尋找空間中的一條二次曲線，該二次曲線分別被投影為C 和C′。由上述分析知道，空間一條二次曲線能夠表示成一個空間錐面和一個平面的交線，因此對于空間二次曲面的射影重建問題就是要根據該二次曲線的圖像來確定空間錐面和該平面的方程。

定理1設攝像機的投影矩陣分別為P 、P′，則連接攝像機中心O、O′和圖像中對應的 二次曲線C 和C′的錐面方程Q 和Q′分別是

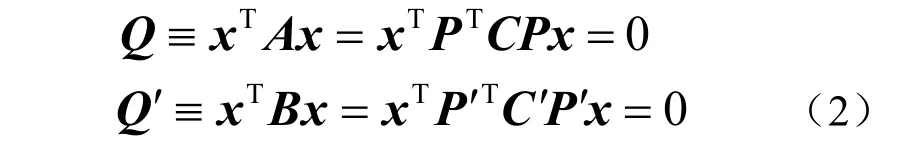
證 明將對應于兩個攝像機的投影方程分別代入二次曲線的二次型方程便可得到式(2)。式(2)表示如果空間點x 的投影位于圖像二次曲線C （或C′）上，則x 滿足式(2)，而且任何位于由O 和C 組成的錐面（或O′和C′組成的錐面）上的點的投影都位于C （或C′）上，因此 式(2)分別為Q 和Q′的錐面方程。

考慮二次曲面束 Q + λQ ′=0，對于每一個λ 的值，方程 Q + λQ ′=0表示一個二次曲面，該曲面通過Q 和Q′所有的公共點。該曲面束中的所有二次曲面的公共點組成一條曲線，該曲線是Q 和Q′交線，并且這條曲線就是該曲面束的 基曲線。兩個二次曲面的基曲線一般是一條四次曲線。在本文中，重建約束就是限定這對對應的錐面在空間的交線是一條二次曲線。

由于空間的這條二次曲線是基曲線的一部分，因此束的基曲線就被分為兩部分，其中的一部分就是空間的這條二次曲線，同時另外一部分也是一條二次曲線。由于一對平面可以被看作秩為2 的退化的二次曲面，這對退化的二次曲面就組成了一對屬于二次曲面束中的一對平面。所以，從兩個圖像中重建空間二次曲線就等同于尋 找一個λ，使得λ 矩陣 C (λ ) = A+λB的秩為2，此時， xTAx =0和 xTBx =0就是對應于空間二 次曲線的錐面。

1.3 射影重建的對應條件

命題1 對于一對對應二次曲線存在兩個獨立的多項式條件。

證 明一個4×4 的對稱矩陣有10－1＝9個自由度，這樣一個矩陣束就有9－1＝8 個自由度；同時，一個秩為2 的4 階對稱矩陣有6 個自由度，于是對于一對對應二次曲線就有8－6＝2個獨立條件。

現在推導這兩個多項式條件。

考慮λ 矩陣 C (λ ) = A+λB的特征多項式

由于 ( )λC 是一個4×4 的是對稱矩陣，要使 得它的秩為2，必須有兩個不同的非零特征值和兩個零特征值，因此對應條件應滿足

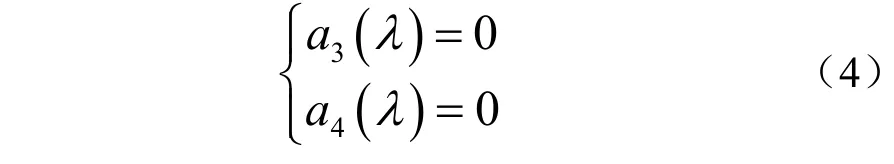
根據定義， a4( λ )是 C (λ )的行列式，這樣a4( λ )就是矩陣束 A + λB的特征多項式，并且

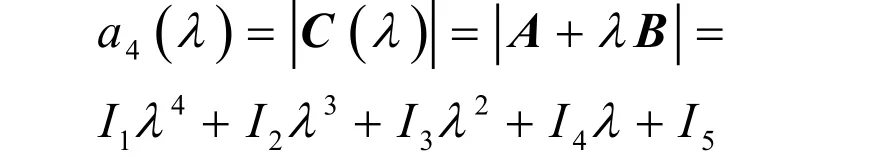
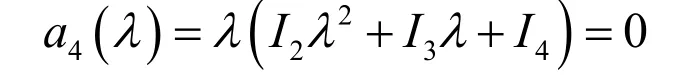
一般情況下， a4( λ )= 0有四個根，每一個 根是束中的一個特征值，并且對應于束中一個矩陣，其中兩個特征值分別是 0=λ 和 ∞=λ ，它們分別對應于矩陣A 和B，其余兩個特征值是下面二次方程的兩個根。

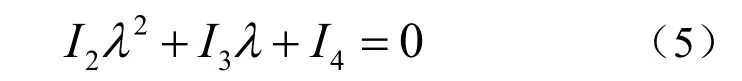
為了在束中有一個秩為2 的矩陣，則必須至少有一個二重特征值，因此式（5）必須有兩個相等的根，即

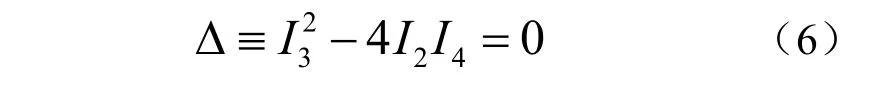
這就是第一個對應條件。

當 a4(λ )= 0的條件被確定之后，下面推導a3( λ )= 0的對應條件， a3( λ )是λ 的一個三次多項式，它可以寫為

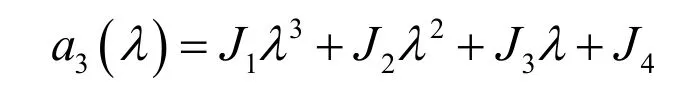
其中ij 是由矩陣A、B 個元素組成的多項式。

第二個對應條件通過將 a3( λ )、a4(λ )兩個 方程聯立起來求解λ，再利用 0=Δ 則很容易得到下面的第二個對應條件

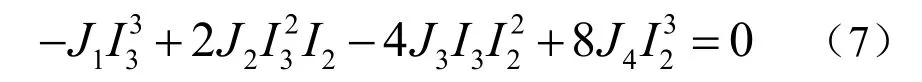
因此，一對對應二次曲線的兩個多項式的對應條件分別是式（6）和式（7）。

1.4 射影重建的計算方法

1.4.1 退化的二次曲面

因為方程（5）有兩個相等的根，所以兩個相等的特征值可直接求得，其中

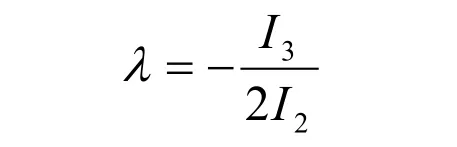
而退化的二次曲面的矩陣 BAC λ+= 。

1.4.2 求解平面對

利用式（7）將矩陣 ( )λC 的特征多項式（3），可以化簡為

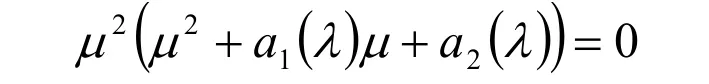
其中兩個非零特征值1μ 和2μ 是下面二次方程的根

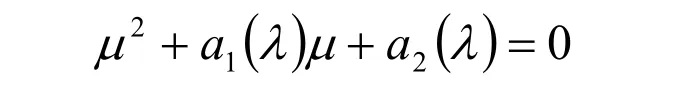
因為C 是一個實對稱矩陣，因此存在一個變換矩陣T ，可以將矩陣C 轉化成一個對角矩陣

相應地將 x = Tx′代入 x′Tdiag ( μ1, μ2,0,0) x′ =0 中，二次曲面 xTCx =0變換為

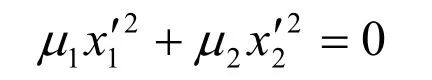
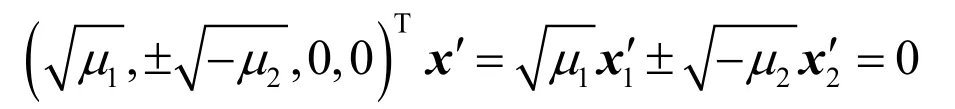
顯然，為了得到實平面，必須使

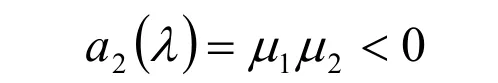
設 21,vv 分別是矩陣C 的特征值 21,μμ 對應的特征向量，則平面對≡x = 0, i =1,2在原始坐標系下的方程為

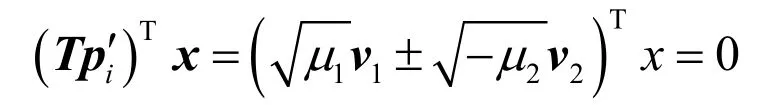
1.4.3 計算步驟

（1） 選擇對應的二次曲線對

第一步 對于每一對二次曲線 iC 和 jC′，組成 錐 面 A = PTCiP 和 B = P ′TCiP ′，計 算I2, I3,I4和 Δi,j；

第二步 在兩幅圖像所有可能的二次曲線 對中選擇 ji,Δ 絕對值最小的像對作為可能對應的 二次曲線對；

（2） 射影重建

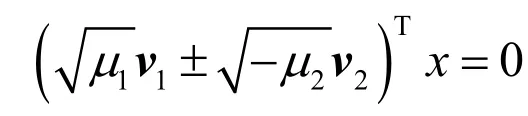
2 實驗驗證

在本文實驗中，使用雙目成像獲得杯子和盤子的兩幅圖像，如圖1 所示。

實驗中的物體共有三條二次曲線，分別是杯子的杯口圓、盤子的外圓和內圓。首先對原始圖像進行邊緣檢測和二次曲線的匹配，匹配后的二次曲線見圖2。

圖1 實驗中的原始圖像

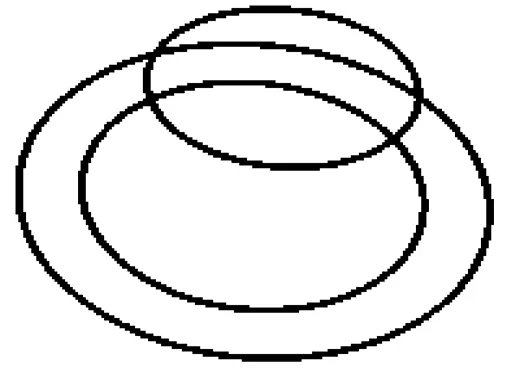
圖2 圖像中的三條二次曲線的匹配

對于兩幅圖像中的每一對二次曲線計算Δ，計算結果見表1。

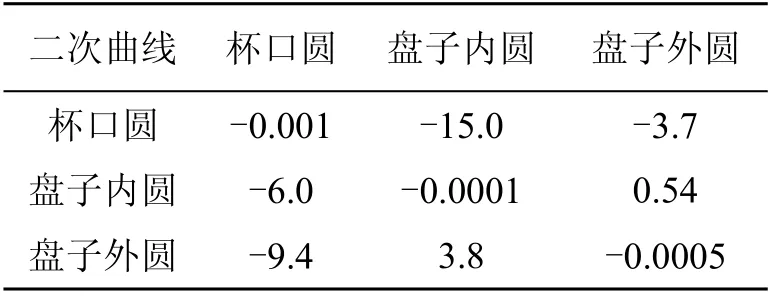
表1 計算兩幅圖像中的每一對二次曲線Δ

空間二次曲線重建結果見表2。

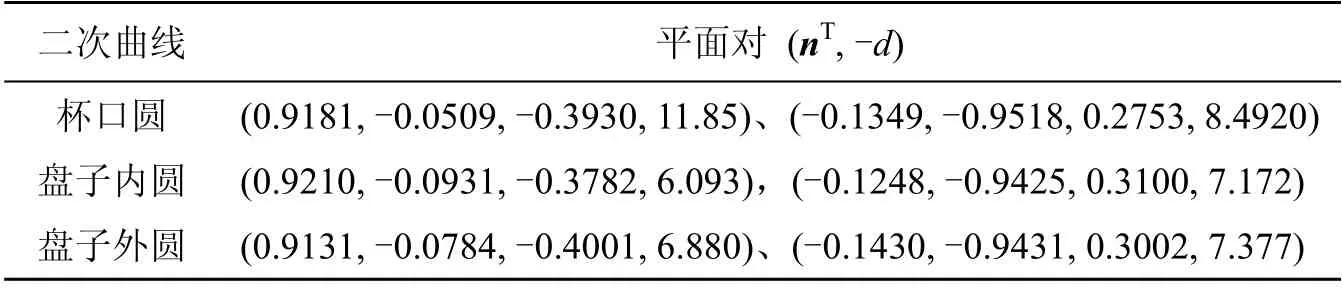
表2 空間二次曲線的重建

利用本文中的計算方法求出了空間二次曲線所在的平面對，而實際杯口圓、盤子內圓、盤子外圓所在的平面是計算結果中平面對中的第一個平面，具體判斷還要利用其它條件，在此不再深入討論。

通過對實驗結果的分析可知，杯口圓和盤子外圓高度差是4.97cm，盤子外圓與內圓的高度差是0.787cm；實際通過測量，杯口圓、盤子外圓、盤子內圓距地面的高度分別是8.5cm、3.0cm、2.3cm，也就是說杯口圓和盤子外圓實際高度差是5cm，盤子外圓與內圓的實際高度差是0.7cm，所以計算結果和實際相符。

3 結 論

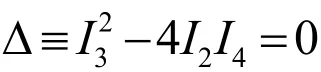
[1] Luong Q T, Faugeras O D. Self-calibration of a moving camera from point correspondences and fundamental matrices [J]. International Journal of Computer Vision, 1997, 22(3)： 261-289.

[2] Cordelia Schmid, Andrew Zisserman. The geometry and matching of lines and curves over multiple views [J]. International Journal of Computer Vision, 2000, 40(3)： 199-233.

[3] Lasenby J, Fitzgerald W J, Lasenby A N, et al. New geometric methods for computer vision： an application to structure and motion estimation [J]. International Journal of Computer Vision, 1998, 26(3)： 191-213.

[4] Carsten Rother, Stefan Carlsson. Linear multi view reconstruction and camera recovery using a reference plane [J]. International Journal of Computer Vision, 2002, 49(2/3)： 117-141.

[5] Yi Ma. A differential geometric approach to multiple view geometry in spaces of constant curvature [J]. International Journal of Computer Vision, 2004, 58(1)： 37-53.

[6] 儲 珺, 高滿屯, 陳 震. 從序列圖像計算二次曲線的光流[J]. 工程圖學學報, 2002, 23(2)： 82-88.

[7] 鐘 集, 唐素蘭, 葉木秀. 高等幾何[M]. 武漢： 武漢大學出版社, 2005. 167-179.