Position Group Contribution Method for Estimation of Melting Point of Organic Compounds

WANG Qiang (王強), MA Peisheng (馬沛生) and NENG Shifeng (能士峰)1,

?

Position Group Contribution Method for Estimation of Melting Point of Organic Compounds

WANG Qiang (王強)1,*, MA Peisheng (馬沛生)2and NENG Shifeng (能士峰)1,2

1School of Material Science and Chemical Engineering, Tianjin University of Science and Technology, Tianjin 300457, China2School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China

A new method is proposed based on the position group contribution additivity for the prediction of melting points of covalent compounds. The characteristics of this method are the use of position distribution function, which could distinguish between most isomers includingorstructure of organic compounds. Contributions for hydrocarbons and hydrocarbon derivatives containing oxygen, nitrogen, chlorine, bromine and sulfur, are given. Results are compared with those by the most commonly used estimating methods. The average derivation for prediction of normal melting temperature of 730 compounds is 14.46 K, compared to 29.33 K with the method of Joback, and 27.81 K with the method of Constantinou-Gani. The present method is not only more accurate, but also much simpler and more stable.

melting point, prediction, position group contribution

1 Introduction

Knowledge of physicochemical properties of organic compounds is essential for predicting their behavior. Melting point is one of the most widely used physical properties in chemical engineering design and experiments. Although vast amount of experimental data are available in literature, but the presence of impurity or thermal instability of some compounds may thwart the experimental measurement. Under such conditions, mathematical models could be used to provide a reasonable estimation of the properties [1-8]. Some of the group contribution methods for estimation of melting points were developed [5-7]. Joback-Reid developed a first-order group contribution method with 40 groups for organic compounds containing halogens, oxygen, nitrogen and sulfur [5]. Constantinou-Gani introduced a two-level group contribution scheme consisting of 63 first-order groups and 40 second-order groups [6]. Marrero-Gani modified this model using the third-order groups that could account for more complex heterocyclic and large polyfunctional alicyclic compounds [7].

The mean absolute errors, number of compounds and compound categories by some of the methods discussed above are listed in Table 1.

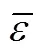
Table 1 Mean absolute errors () in general estimation methods for melting point

As our preliminary work on the critical temperature [22], critical pressure [23], critical volume [24] and the normal boiling point [25] showed significant improvements with respect to the published methods, it was decided to invest further effort into the development of a new group contribution method for melting point of organics. We proposed a position group contribution method for the prediction of critical parameters of organic compounds, in which only the knowledge of their chemical structure is required [22-25]. A most important point must be claimed is that all these propertiesc,c,candbmentioned above andmin this work, are estimated by the same universal position distribution function proposed.

2 Experimental data

Total 730 compounds containing carbon, hydrogen, oxygen, nitrogen, chlorine, bromine and sulphur were used for the determination of group contributions. The detail list is given in Fig. 1, and includes linear and branched alkanes (158), cycloalkanes (41), alkenes (63), aromatics (40), alcohols (66), aldehydes and ketones (67), acids (66), phenols and ether oxides(19), esters (126), chloro and bromoalkanes (25), amines (27), pyridines (10), alkane thiols and thioethers (22).

The experimental data, from the TRC Thermodynamic Tables [26], give the critical properties, normal boiling points and melting points for a large number of hydrocarbons and derivatives. The handbooks by Ma [27] and Poling. [28] also provide an abundance of property data about organic compounds.

3 Computations

3.1 Calculation method

The first step was testing correlations to represent the properties. Only one-parameter contribution was considered for each group at first. The melting point function was constructed by the contributions from all the groups as well as position distribution function. Benson’s second order groups and a few of the third order groups were applied into this works. The details of the group classification are described in Table 2. Here, the melting point is expressed as follows [22].

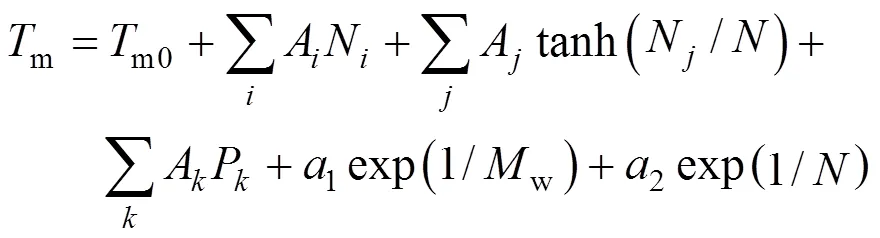
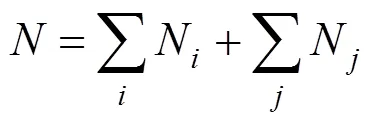
Where parameterAorArevealsorgroup contributions, which allowed the minimization of the residual estimation error by regression.Nrepresents the number of groups in which carbon element forms the centre of the group,Nrepresents the number of groups in which non-carbon element forms the center,is the total number of groups,Pcharacterizes position factor,mois 5963.486 K, andWis the molecular weight.

Moreover, the position corrections were taken into account due to the longer distance interactions. Some corrections for interactions through benzene or pyridinerings were obtained, which was the result in a better distinction between series of chain-branched aromatic isomers. Parameters for five- and six-membered saturated hydrocarbon rings were also determined. We present the correlations that give the best estimations in Table 3.

3.2 Application examples

Some examples for computation ofmfor the organics are given follows.

Example 1 Estimation of the melting point of 2,4,5-trimethylbenzoic acid

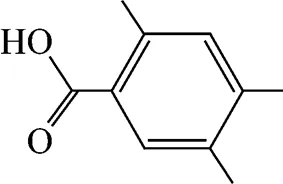
This compound is decomposed into the position groups as follows:

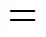
2correction; 2correction

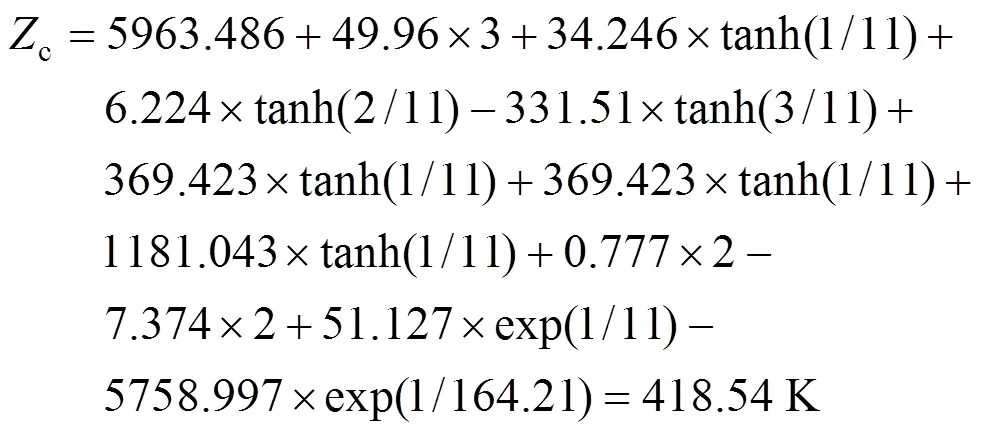
The calculated result is 418.54 K while the experimental melting point is 425.15 K.

Example 2 Estimation of the melting point of diethyl pimelate

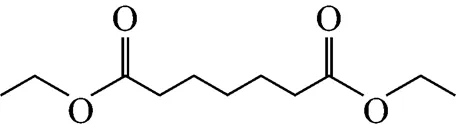
This compound is decomposed into the position groups as follows:

From the contributions in Table 2, the melting point can be calculated from Eq. (1).

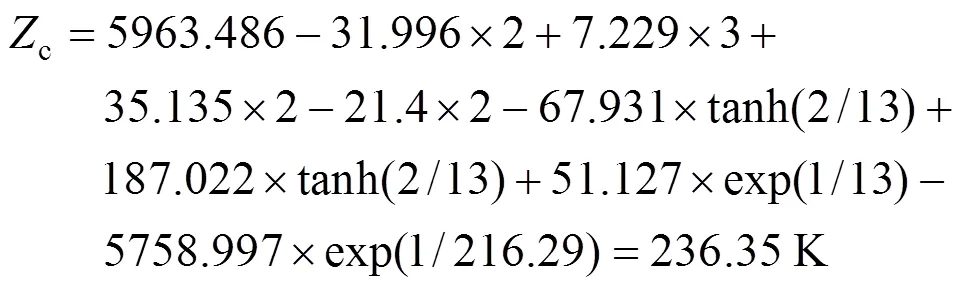
The calculated result is 236.36 K while the experimental melting point is 249.15 K.

Example 3 Estimation of the melting point of 2,6-dimethyl-4-heptanone

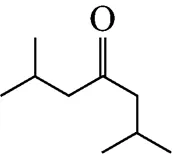
This compound is decomposed into the position groups as follows:

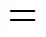
From the contributions in Table 2, The melting point is estimated by Eq. (1):

The calculated result is 217.63 K, while the experimental melting point is 227.15 K.

Table 2 Position group contributions for the prediction of Tm

Table 2 (Continued)

①andcorrections consider interactions between alkyl chains through a benzene ring.

② Corrections for pyridines:,andpyridine corrections take into account alkyl ligands in position,andwith respect to the N element, respectively.

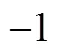
4 Results and Discussion

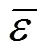
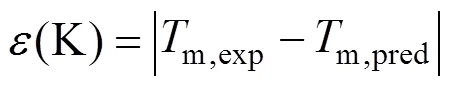
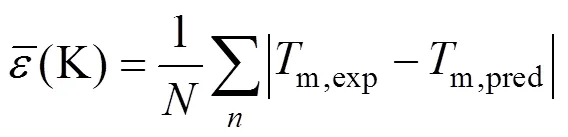
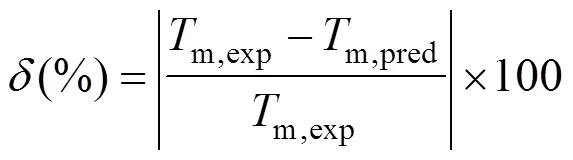
Figure 1 reports results for the 730 compounds considered in this study and compares our prediction for melting points with experimental data.

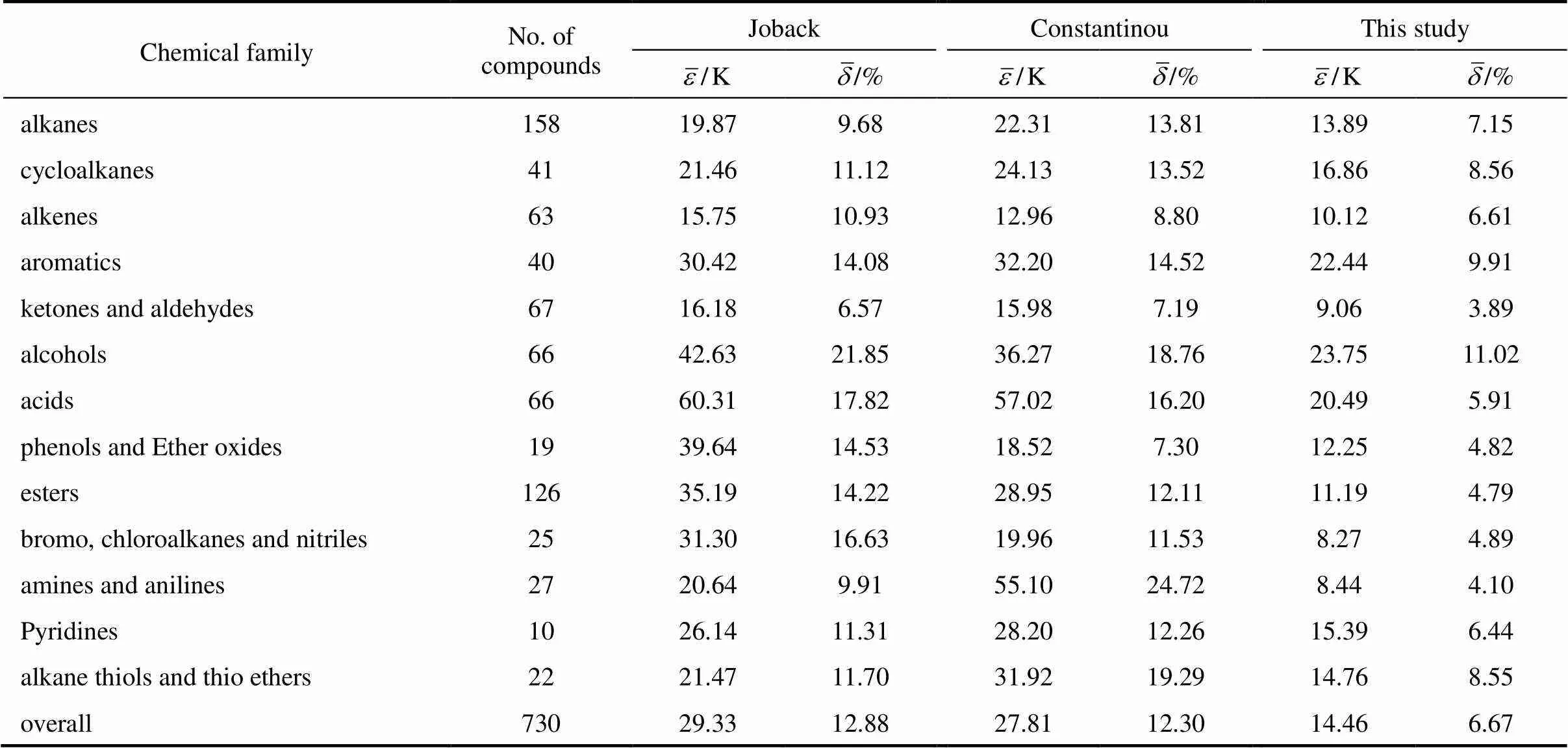
Table 3 Comparison of Tm predicted by our model with those methods of Joback and Constantinou

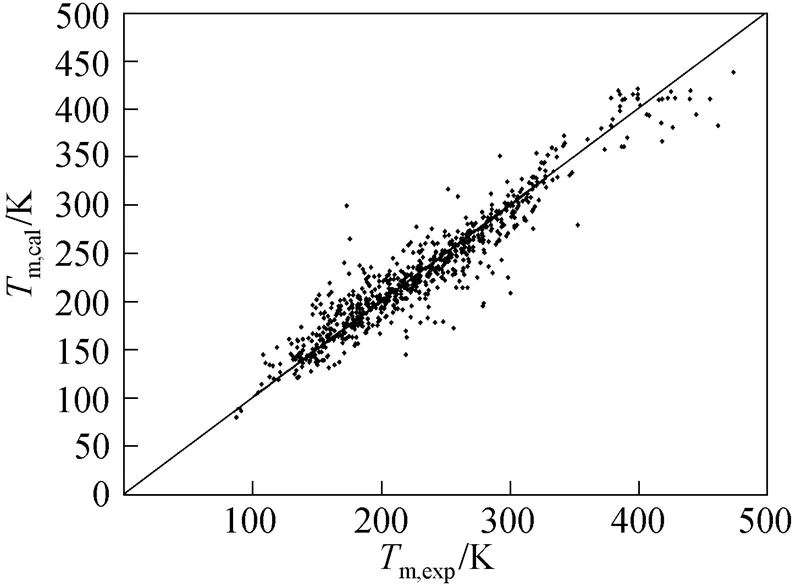
Figure 1 Comparison of melting point temperature calculated from this study with experimental values

One complementary set of position group contributions was developed for the predictive estimation of melting points of organic compounds. The second order groups defined by Benson, which have long been recognized as more accurate than the first order groups for thermochemical predictions, were used for this purpose. Position factor could distinguish between most isomers including- or-structure of organic compounds for their properties. Contributions for compounds containing carbon, hydrogen, oxygen, nitrogen, sulphur, chlorine and bromine were reported, and the results were evaluated with respect to other predictive methods. The presents melting points show an average deviation about 14.46 K, much less than those from the well known method of Joback-Reid and Constantinou-Gani well as all other estimation methods.

5 ConclusionS

A new position group contribution method recently proposed by our laboratory for the estimation of the critical temperature, critical pressure, critical volume and normal boiling point is extended to the prediction of melting point of organics. Contributions for compounds containing carbon, hydrogen, oxygen, nitrogen, chlorine and sulphur are reported, and the position distribution function is developed, which could distinguish between the thermodynamic properties of most isomers of organic compounds including- and- or- and- structures. The results indicate that our model provides very satisfactory results. The average difference for melting point predictions of 730 organic compounds is 14.46 K and 6.67 %. The higher prediction accuracy of the proposed method shown in our previous works and this work suggests that it is possible to use a same framework to predict the critical properties of organic compounds containing various functional groups.

1 Jain, A., Yalkowsky, S.H., “Estimation of melting points of organic compounds-II”,.., 95, 2562-2618 (2006).

2 Li, H.D., Higashi, H., Tamura, K., “Estimation of boiling and melting points of light, heavy and complex hydrocarbons by means of a modified group vector space method”,, 239, 213-222 (2006).

3 Jain, A., Yalkowsky, S.H., “Comparison of two methods for estimation of melting points of organic compounds”,...., 46 (8), 2589-2592 (2007).

4 Sanghvi, R., Yalkowsky, S.H., “Estimation of normal boiling point of organic compounds”,...., 45, 2856-2861 (2006).

5 Joback, K.G., Reid, R., “Estimation of pure-component properties from group-contributions”,..., 57, 233-243 (1987).

6 Constantinou, L., Gani, R., “A new group contribution method for estimation of properties of pure compounds”,., 40, 1697-1710 (1994).

7 Marrero, J., Gani, R., “Group-contribution based estimation of pure component properties”,., 183/184, 183-208 (2001).

8 Guha, R., Jurs, P.C., “Determining the validity of a QSAR model”,..., 45, 65-73 (2005).

9 Trohalaki, S., Patchter, R., Drake, G.W., Hawkins, T., “Quantitative structure property relationships for melting point and densities of ionic liquids”,, 19, 279-284 (2005).

10 Katritzky, A.R., Maran, U., Karelson, M., Lobanov, V.S., “Prediction of melting points for the substituted benzenes: A QSPR approach”,...., 37, 913-919 (1997).

11 Charton, M., Charton, B., “Quantitative description of structural effects on melting points of substituted alkanes”,...., 7, 196-206 (1994).

12 Katritzky, A.R., Gordeeva, E.V., “Traditional topological indiceselectronic, geometrical, and combined molecular descriptors in QSAR/QSPR research”,....., 33, 835-857 (1993).

13 Katritzky, A.R., Lomaka, A., Petrukhin, R., Jain, R., “QSPR correlation of the melting point for pyridinium bromides, potential ionic liquids”,....., 42, 71-75 (2002).

14 Katritzky, A.R., Jain, R., Lomaka, A., Petrukhin, R., Maran, U., Karelson, M., “Perspective on the relationship between melting points and chemical structure”,, 1, 261-265 (2001).

15 Chickos, J.S., Nichols, G., “Simple relationships for the estimation of melting temperatures of homologous series”,...., 46, 562-573 (2001).

16 Karthikeyyan, M., Glen, R.C., Bender, A., Bender, A., “General melting point prediction based on a diverse compound data set and artificial neutral networks”,..., 45, 581-590 (2005).

17 Tsakanikas, P.D., Yalkowsky, S.H., “Estimation of melting point of flexible molecules: Aliphatic hydrocarbons”,..., 17, 19-33 (1988).

18 Simamora, P., Yalkowsky, S.H., “Group contribution methods for predicting the melting point and boiling point of aromatic compounds”,...., 33, 1405-1409 (1994).

19 Krzyzaniak, J.F., Myrdal, P., Simamora, P., Yalkowsky, S.H., “Boiling point and melting point prediction for alphatic nonhydrogenbonding compounds”,...., 34, 2530-2535 (1995).

20 Zhao, L., Yalkowsky, S.H., “A combined group contribution and molecular geometry approach for predicting melting point of alphatic compounds”,...., 38, 3581-3584 (1999).

21 Yalkowsky, S.H., Dannenfelser, R.M., Myrdal, P.B., Simamora, P., Mishra, D.S., “Unified physical property estimation relationships (UPPER)”,, 28, 1657-1673 (1994).

22 Wang, Q., Ma, P.S., Jia, Q., “Position group contribution method for the prediction of critical temperature of organic compounds”,..., 53, 1103-1109 (2008).

23 Wang, Q., Jia, Q., Ma, P.S., “Position group contribution method for the prediction of critical pressure of organic compounds”,..., 53, 1877-1885 (2008).

24 Jia, Q., Wang, Q., Ma, P.S., “Position group contribution method for the prediction of critical volume of organic compounds”,..., 53, 2606-2612 (2008).

25 Wang, Q., Ma, P.S., “Position group contribution method for the prediction of normal boiling point of organic compounds”,...., 17 (2), 254-258 (2009).

26 Frenkel, M., Gadalla, N.M., Hall, K.R., Hong, X., Marsh, K.N., Wilhoit, R.C., TRC Thermodynamic Tables: Hydrocarbon; Non-Hydrocarbon, Thermodynamic Research Center, The Texas A&M University System (1997).

27 Ma, P.S., Handbook of Property Data of Organic Compound, Chemical Industry Press, Beijing (2006).

28 Poling, E.B., Prausnitz, J.M., O’Connell, P.J., The Properties of Gases and Liquids, 5th edition, McGraw-Hill, Inc., New York (2001).

2008-11-11,

2009-02-25.

* To whom correspondence should be addressed. E-mail: wang_q@tust.edu.cn