灰色關聯度法在地下水脆弱性評價與分區中的應用

孫豐英，許光泉，唐文鋒

（1. 安徽理工大學，淮南 232001；2. 淮南聯合大學，淮南 232038）

灰色關聯度法在地下水脆弱性評價與分區中的應用

孫豐英1，許光泉1，唐文鋒2

（1. 安徽理工大學，淮南 232001；2. 淮南聯合大學，淮南 232038）

采用灰色系統理論中的灰色關聯度分析方法對地下水脆弱性進行研究，選取地下水位埋深、包氣帶巖性、含水層砂層厚度等6個因子建立了脆弱性評價指標體系，采用離差最大化方法確定評價指標的權重，使權重的分配有了一定的理論依據。并以MATLAB為平臺編制了常用計算程序，應用于撫州市地下水脆弱性評價與分區，取得良好結果。

灰色關聯度；地下水脆弱性；指標體系；離差最大化方法

0 引言

“脆弱性”是系統失穩后產生后果的嚴重性，是災害形成的根源[1]。地下水脆弱性反映了地下水系統遭受污染的潛在可能性，污染物在不同的地下水系統中具有不同的遷移轉化能力，目前缺乏這方面的系統研究。要有效控制地下水污染，必須研究不同地下水系統的脆弱性。

影響地下水脆弱性的潛在因素很多，要想建立一個包含所有影響因素的評價因子體系在實際應用中是不現實的[2]。首先因子越多，因子之間的關系也就越復雜，容易造成因子之間相互關聯或包容（如含水層的水動力傳導系數與含水層巖性密切相關）；其次，有些因子（如土壤成分、含水量、粘土礦物含量等）在區域性評價中取值比較困難，可操作性較差；另外因子太多，也會沖淡主因子的影響。

灰色系統理論提出的灰色關聯分析，可在不完全的信息中對要分析研究的各因素，通過一定的數據處理，在隨機的因素序列間，找出它們的關聯性。因此，特別適合像地下水脆弱性這類數據有限、沒有模型、復雜而且具有不確定性問題的分析和評價。灰色關聯分析是一種多因素統計分析法，它以各子因素時間序列與母因素時間序列數據為基礎計算母子因素的關聯度，用關聯度來描述母子因素間關系強弱、大小和次序[3]。

(1) 灰色關聯度算法

制定一個參考數據：

x0(x0=(x0(1),x0(2), ... x0(n))),

有m個比較數據列：

x1,x2,...xm(xi=(xi(1),xi(2),...xi(n));i=1,2,...,m)。

按下式計算xi相對于x0在第j個元素上的關聯系數[4](j=1,2,...,n)

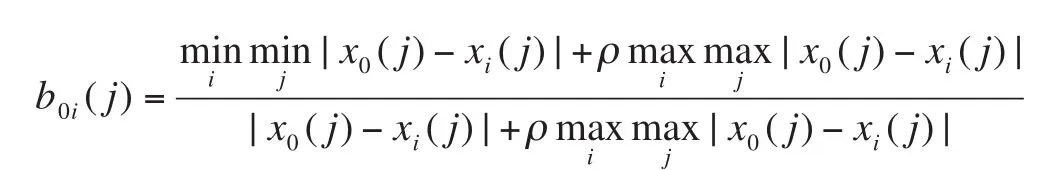
式中：ρ為分辨系數，其取值的大小可以控制對數據轉化的影響，通常在(0,1)內取值。一般情況下取ρ=0.4，越小越能提高關聯系數間的差異。

從上式關聯系數計算得到的是各比較序列與參考序列在各點的關聯系數值，結果較多，信息過于分散，不便于比較，因此，有必要將每一個比較數列各個時刻的關聯系數集中體現在一個數值上，即灰色關聯度。一般可采用求平均值或加權求和的方法[4]，求出xi對x0的關聯度：

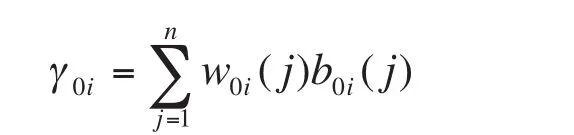
其中， 是比較序列與參考序列在第j個指標的權系數，利用離差最大化來計算[5]。

(2) 算法的MATLAB實現

為了計算方便，筆者以MATLAB為平臺開發了無量綱化的Matlab程序、計算關聯系數矩陣的Matlab程序以及離差最大化求權重等函數程序。因篇幅所限，僅給出離差最大化計算權重的Matlab程序。

1 灰色關聯度應用于撫州市地下水脆弱性評價與分區

撫州市位于江西省東部，撫河中游。研究區地理坐標為東經116°15′ 116°22′，北緯27°57′28°01′。區內海拔標高40～60m，發育一、二、三級階地，為第四系沖積層覆蓋。一、二級階地具有明顯的雙層結構，上部為0.5～2m厚的粉細砂層或耕作層，下部為4～6m厚的砂礫石層。三級階地上部為4～9m厚的紅粘土層，下部為少量砂礫石。

為了取得較準確的資料，針對區內地質地貌、工農業布局、水系及污染情況，在撫河、宜黃河流域的不同地段均衡取點，共布置20個地下水監測點。

（1）DITRQP評價模型

在進行指標選取時，遵循指標的穩定性、獨立性、可比性和易操作性原則[6～8]。此次地下水脆弱性評價指標包括地下水埋深（D），包氣帶巖性（I），淺層地下水含水層砂層厚度（T），含水層的補給強度（R），地下水水質現狀（Q）和污染源（P）等。

本文地下水脆弱性評價模型為經過修改的DRASTIC模型[9,10]：

DrDw+IrIw+TrTw+RrRw+QrQw+PrPw=DITRQP

式中：下標r為劃分等級，Dr為r等級量化值，Dw為權重，DITRQP為評價綜合指數。

地下水埋深、淺層含水層砂層厚度、地下水質量等與地下水脆弱性呈負相關性，值越大，評分越低；含水層的凈補給、降水入滲系數與地下水脆弱性呈正相關性。以0.2作為等級劃分間隔，將地下水資源脆弱性劃分為五個等級，根據以上各評價指標與地下水脆弱性關系，進行如下量化分級（表1）。

表1 地下水脆弱性評價指標的量化值

（2）網格剖分與編號

進行網格剖分是將空間大區域劃分為小的統計單元，以便于數據的獲取和樣本空間的統計。本文根據研究區面積和數據的精度，對研究區進行間距為0.1km×0.1km正方形網格剖分，剖分單元共計5980個（圖1）。

圖1 研究區網格剖分圖

（3）評價結果

設k為研究樣本的序號，即區內20個監測點。k0為各評價指標的最優值，作為標準參考數據列，即k0=[0.5；0.4；1.4；18.0；0.8；0.9]，利用上述方法進行灰色關聯度計算，其原始數據及評價結果見表2。

表2 地下水脆弱性評價指標測點數據及評價結果

應用上述的離差最大化方法確定的各指標的權重w為：w =[0.167，0.146，0.170，0.193，0.186，0.137]，表明此6個評價指標對地下水脆弱性的影響程度為：含水層的凈補給＞地下水質量＞含水層砂層厚度＞地下水埋深＞包氣帶巖性＞污染源。

由表2可以看出灰色關聯度算法算得的結果跟運用RBF神經網絡法計算的結果基本吻合，進一步說明了灰色關聯度算法的可靠性。

最后將算得的DITRQP模型綜合評價指數結果通過內插法分配到各評價單元[11,12]，利用MAPGIS的空間分析和編輯功能完成地下水脆弱性分區，如圖2。

圖2 地下水脆弱性評價分區示意圖

高脆弱區大致分布在河流兩岸和主城區一帶，沿河兩岸呈帶狀分布組成一、二級階地，為松散巖類孔隙含水層，地下水位埋深較淺。一般脆弱區主要分布在區內的東北部、主城區邊緣及撫北等地，本區具有明顯的雙層結構，地下水天然保護條件好。低脆弱區分布在南部及撫北部地區，人口稀疏，遠離市區和工業區，污染物滲入地下的量較少，即使有污染因子，也由于地下水的不停交替與淡化作用，使其脆弱性程度相對最低。

2 結語

（1）選用灰色關聯度方法進行地下水脆弱性評價與分區，使用的數據量較一般的函數相關性分析和回歸分析的要求較少而分辨率高，回避了不同指標的數量集和量綱，具有很好的擴展性。

（2）利用灰色關聯度方法進行研究，并與人工神經網絡結果進行比較，結果基本一致。撫州市的應用實踐表明：所得結果具有較好的客觀性，是提高地下水脆弱性評價與分區客觀度的一種有效途徑。

[1] 商彥蕊，史培軍等.人為因素在農業災害形成過程中所起作用的探討——以河北省旱災脆弱性研究為例[J].自然災害學報,1997(4):35～43.

[2] Vrba J, Zaporozec A. Guidebook on mapping groundwater vulnerability[M]. International Association of Hydrogeologists (International Contributions to Hydrogeology 16),Verlag Heinz Heise, Hannover, 1994.106.

[3] 劉思峰,黨耀國,方志耕.灰色系統理論及其應用[M].北京:科學出版社,2000:78～101.

[4] 謝乃明,劉思峰.離散GM(1,1)模型與灰色預測模型建模機理[J].系統工程理論與實踐,2005(1)：93～99.

[5] 王應明. 運用離差最大化方法進行多指標決策與排序. 軟科學研究, 1998（3）：36～38，65.

[6] 孫才志,林山杉.地下水脆弱性概念的發展過程與評價現狀及研究前景[J].吉林地質，2000, 19 (1): 30～36.

[7] 吳登定,謝振華等.地下水污染脆弱性評價方法[J].地質通報,2005,24(10):1044～1046.

[8] Soutter Marc, Musy Andre. Coupling1D Monte-Carlo simulations and geo statistics to assess groundwater vulnerability to pesticide contamination on a regional scale [J].Journal of contaminant Hydrology，1998，32:35～39.

[9] 王國利,周惠成,楊 慶.基于DRASTIC的地下水易污染性多目標模糊模式識別模型.水科學進展,2002,11(2):173～179.

[10] Gogu R C, Dssargues A. Current trends and future challenges in groundwater vulnerability assessment using overlay and index methods[J]. Environmental Geology,2003,39(6):549～561.

[11] 周 磊.北京城近郊區地下水脆弱性研究[D].吉林大學碩士學位論文,2004.9.

[12] 雷 靜.地下水環境脆弱性研究[D].清華大學碩士學位論文,2002,11～14.

Abstract:The different engineering geological problems of foundation pit excavation will occur in the different geological-engineering condition. In this paper, the author discusses the different geologic problems during excavating the foundation pit, and puts forward the detailed countermeasures in a foundation pit project in Xi’an City.

Keywords:groundwater flow into foundation pit; side slope slippage; settlement; timbering; precipitation

Application of the Method of Gray Correlation in Groundwater Vulnerability Assessment and Partitioning

SUN Fengying1, Xu Guangquan1,Tang Wenfeng2
(1. Anhui University of Science and Technology, Huainan, Anhui 232001. 2. Huainan Union University, Huainan, Anhui, 232038 )

The Grey Correlation Method is employed to analyze the vulnerability of groundwater. This paper established an assessment index system, which was made up of the depth to groundwater, impact of the vadose zone, aquifer thickness, net recharge, groundwater quality, and pollutant headwater. The weight allocation is more reasonable by applying the method of maximizing deviation to determine. Moreover, based on the MATLAB, it developed several calculation programs. On the attempt to assess and partition the groundwater vulnerability in Fuzhou City of Jiangxi Province, the result is satisfactory.

gray correlation;groundwater vulnerability;index system; maximizing deviation method

Research on Geologic Problem and Countermeasure of Foundation Pit for a Excavation Project in Xi’an City

GUO Zhifeng
(Shenzhen Construction Engineering Group Co. Ltd., Shenzhen, Guangdong 518048)

P641

A

1007-1903(2009)03-0032-04

孫豐英(1979 -),女,安徽理工大學水文系教師，主要從事環境地質、水文地質方面的教學和科研。