簡易導管的數值計算及分析

1 引 言

導管螺旋槳是特種推進器的一種，早在30年代就已經出現了,主要是為了提高功率系數Bp較高的高負荷螺旋槳的效率。它是在普通螺旋槳的外圍裝上一個套筒,套筒的縱剖面為機翼型或折角線型。這個套筒就稱為導管,套筒可以是固定的,稱為固定導管;也可以是轉動的,稱為轉動導管。轉動導管除了起導流作用外,還起著舵的作用。它有許多種形式,從導管中流場分有2種,包括加速型導管和減速型導管。導管中的螺旋槳工作時,與導管形成了—個整體,這時的流場與沒有導管時的不同。對于加速型導管,首先,可以使螺旋槳盤面處的水流加速,使螺旋槳工作在較大的速度場,從而可以提高螺旋槳的效率。其次,由于導管出口處的面積逐漸擴大,尾流的收縮極小,使軸向誘導速度減小,也有助于提高螺旋槳的效率。最后,由于葉梢和導管的間隙很小,由葉面和葉背的壓力差引起的繞流大大減小,其能量損失也就減小。正是由于這些原因，加速導管螺旋槳具有效率高,推力大,在風浪中的性能較好等特點。對于功率系數Bp較高的高負荷螺旋槳,采用它所能達到的效率,將遠遠超過常規螺旋槳,特別是在系泊情況下,可將系泊推力提高30%以上。

國外發表的導管螺旋槳系列試驗資料中，以荷蘭船模試驗池的No.19A+Ka螺旋槳系列最為著名。隨后，為改善后退性能又提供了No.37+Ka螺旋槳系列，其結果都已繪制成Bp-δ型設計圖譜可供應用。國內對導管螺旋槳的研究也相當活躍。中國船舶科學研究中心通過對2組6個不同剖面的導管與螺旋槳系列的敞水試驗，研究了導管各種幾何參數對導管槳性能的影響，并推薦了性能優良的導管螺旋槳系列。上海交通大學船舶流體力學研究室根據使用單位的要求簡化導管的加工工藝，在系列研究基礎上推薦了2組簡易導管螺旋槳系列，即JD75+Ka螺旋槳系列和JD7704+Ka系列[1]。由于其加工方便，而性能又與機翼型導管相接近，故為不少單位所采用。

Fluent公司近年來推出的流體力學軟件Fluent可廣泛用于水流、氣流、熱流、化學反應、混合流，甚至固液混合反應的分析[2]，并有多種圖文并茂的結果輸出，非常適用于對導管性能的分析，并有可能用數值分析的方法，而不是試驗方法對其尺度、幾何參數等進行優化。這必將降低設計成本，提高工作效率。

由于本文所要應用的導管有特定尺度條件限制，上述文獻提供的性能優良的導管并不能滿足應用要求，故本文在優良導管形狀的基礎上選取幾何參數，利用Fluent軟件對其流場進行數值計算。并計算分析了在不同前緣收縮系數、后緣擴張系數、平行中體長度以及不同長徑比條件下設計導管的推力系數、升阻比和流場分布等。最后通過以上的計算分析各參數對導管水動力性能的影響，從而挑選出滿足條件的較優的導管形狀。

2 導管的幾何特征

由于所設計導管推進器主要用于低速時的推進，負荷比較大，根據導管螺旋槳特點，具有接近JD75導管幾何特征參數的導管比較合適。

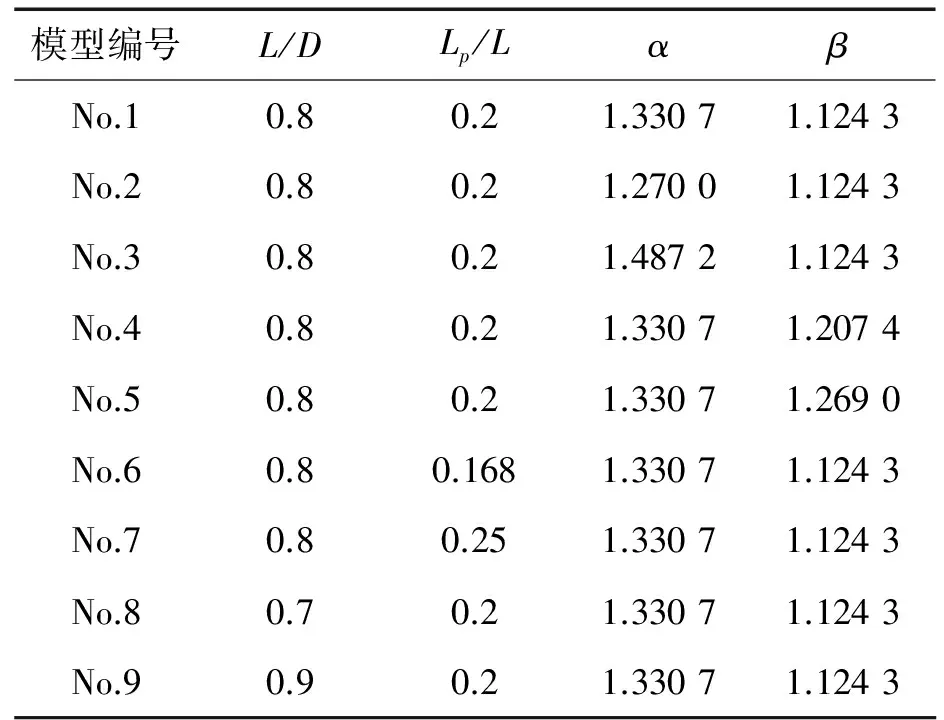
如圖1所示，表征導管特征的幾何參數主要有以下幾個：長徑比L/D、平行中體與導管長度比Lp/L、收縮系數α=A1/A0、擴散系數β=A2/A0(A1,A2,A0分別是導管相應位置的截面積)。為探討導管幾何形狀對導管水動力性能的影響，選擇JD75導管的幾何參數作為參考，以一定規律變化L/D、Lp/L、α、β，生成系列導管。變化范圍局限于前文提到的現有導管的幾何參數，共計9個導管形狀，參數見表1。

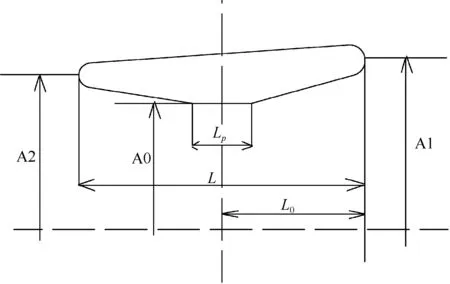
圖1 導管剖面幾何尺寸示意圖

表1導管幾何參數

模型編號L/DLp/LαβNo．10．80．21．33071．1243No．20．80．21．27001．1243No．30．80．21．48721．1243No．40．80．21．33071．2074No．50．80．21．33071．2690No．60．80．1681．33071．1243No．70．80．251．33071．1243No．80．70．21．33071．1243No．90．90．21．33071．1243

3 利用Fluent軟件對導管進行數值模擬與分析

3.1 建模

以JD75導管幾何參數作為設計基礎，均取槳盤面距前緣距離與導管長度比：Lo/L=0.4，并取槳盤處直徑為820 mm，建立模型A1，以此作為導管計算的參考標準。

A1模型參數如下：

長徑比L/D： 0.8

平行中體與導管長度比Lp/L： 0.2

收縮系數α： 1.330 7

擴張系數β： 1.124 3

3.2 計算條件[3]

1) 根據相對性原理,假定導管靜止不動,水流以一定的速度從前方流向導管，Va為流經導管的進速；

2) 計算區域

考慮到計算機的計算能力和計算模型的可靠性[4],計算域如圖2所示。根據流場的對稱性,二維計算只取導管剖面的一半進行計算，并在槳軸中心線的位置取對稱條件。外輪廓線為計算邊界，輪廓線之間是水流流動區域。為保證流場充分發展，長度方向導管的上游及下游分別取10L，高度方向導管外側也取10L。

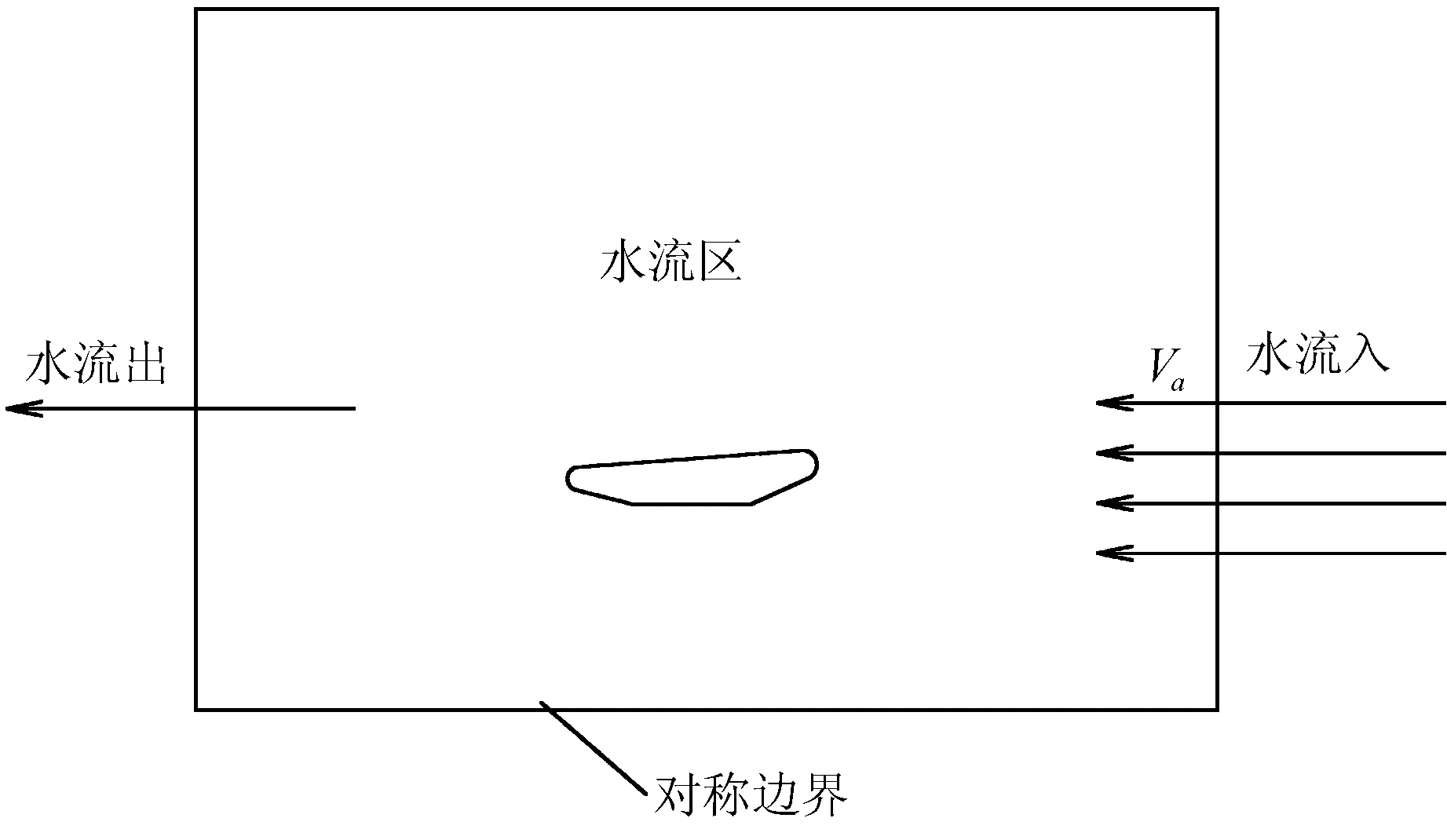
圖2 二維計算域示意圖

三維模型的計算域如圖3所示。取一個包圍四分之一導管的四分之一圓柱，其范圍的選取與二維相仿。

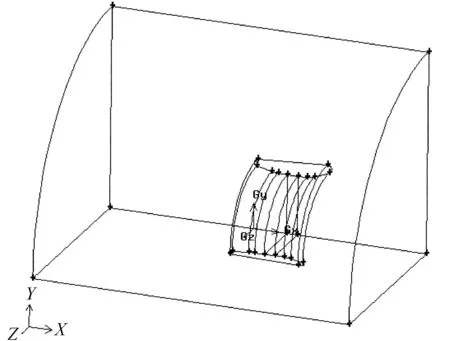
圖3 三維計算域示意圖

3) 邊界條件

計算域的入口采用速度入口條件，即給定速度的大小和方向余弦。計算域的出口采用自由流出，導管表面采用固壁面條件，對稱邊采用對稱條件。

4) 網格劃分

理論上網格劃分的越細,計算點距越小,計算效果越理想[5,6]。實際上Fluent主要用差分法和迭代法解N-S方程,計算精度受到計算機計算能力的影響,需要采取一個折衷的辦法。本文的計算取近壁面邊界層第一層網格高度為10-3倍的L，近壁處理采用標準壁面函數法，經計算檢驗其Y+值(Fluent中為了標識粘性底層與對數律層的分界點而引入的無量綱長度參數)可以控制在60以下，即保證了第一網格到壁面距離在對數區內。因為Fluent允許對稱結構只算一半,故這樣的計算精度既在個人計算機的計算能力允許之內,又能在總體上一定程度地準確反映出導管周圍的流場情況。二維和三維網格劃分分別如圖4、圖5所示。

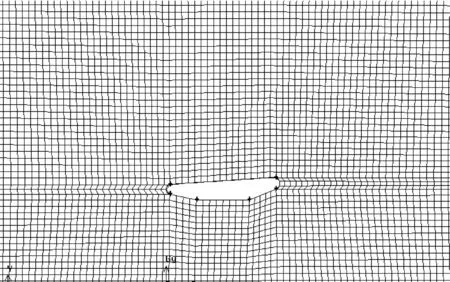
圖4 二維模型導管周圍網格

圖5 三維模型導管周圍網格

3.3 計算結果

通過計算，得到了二維模型的升阻比和三維模型的推力、推力系數和流場分布。圖6為No.1導管切面沿弦長方向各點壓力系數分布曲線。圖中黑線為導管外表面壓力系數，灰線表示導管內表面壓力系數。圖7是其中一個導管推力的試驗結果與計算結果對比圖，對比結果表明了計算方法的有效性。

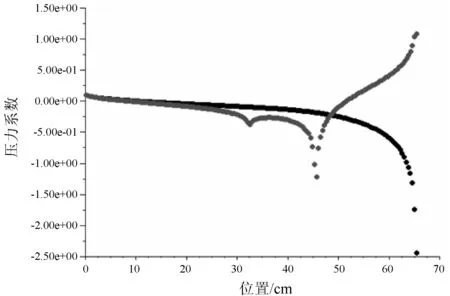
圖6 No.1導管切面壓力系數分布曲線

圖7 導管推力的試驗結果與計算結果對比

4 結果分析

在No.1模型的基礎上，以一定規律變化L/D、Lp/L、α、β，生成系列導管，共 9個導管形狀，其幾何參數見表1。

由圖8知，在J=0.3(設計工況)附近，各個導管之間的升阻比關系如下：

1) No.3>No.2>No.1 (表明α的影響)

2) No.4>No.5>No.1 (表明β的影響)

3) No.7>No.1>No.6 (表明Lp/L的影響)

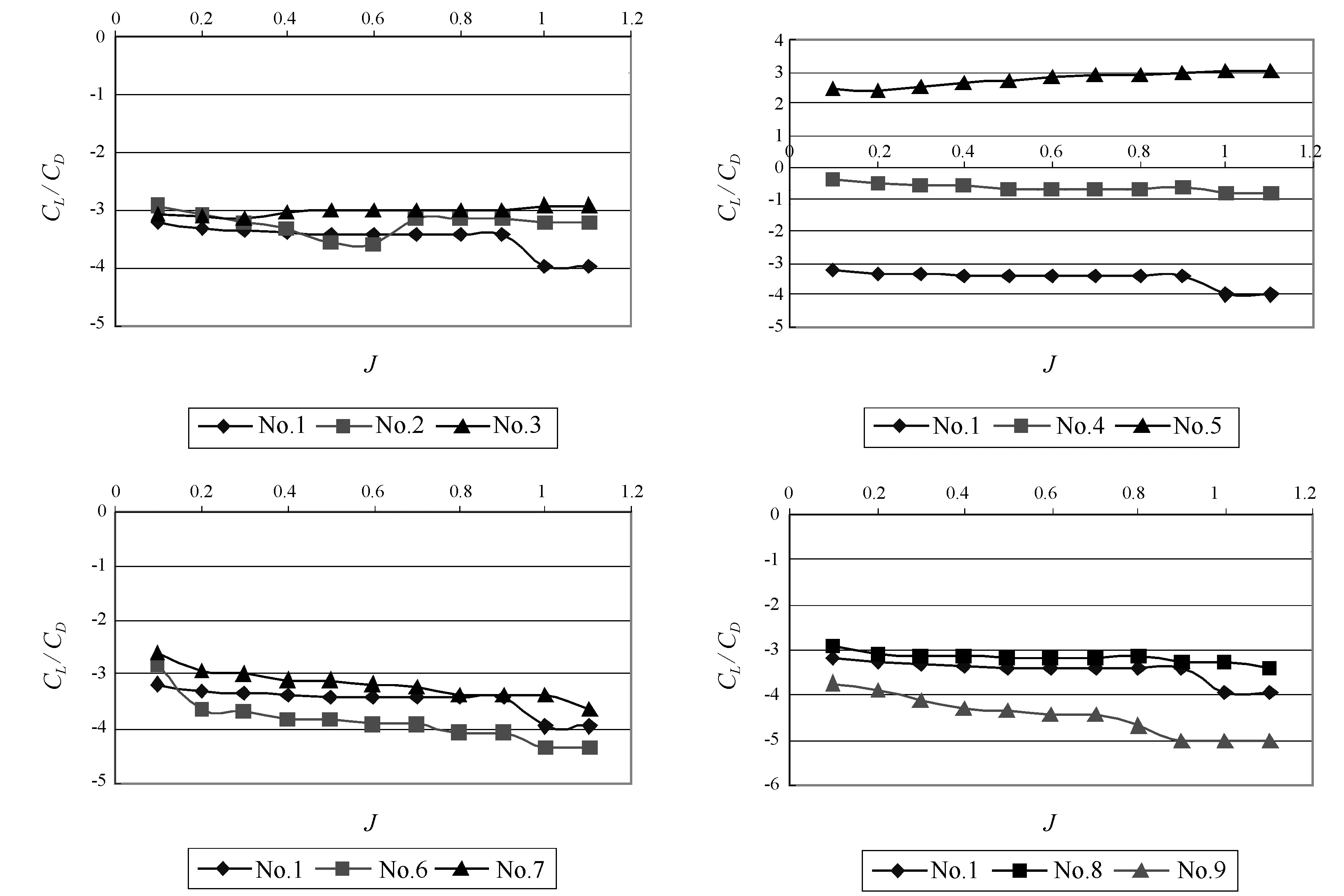
圖8 模型No.1～No.9升阻比曲線圖

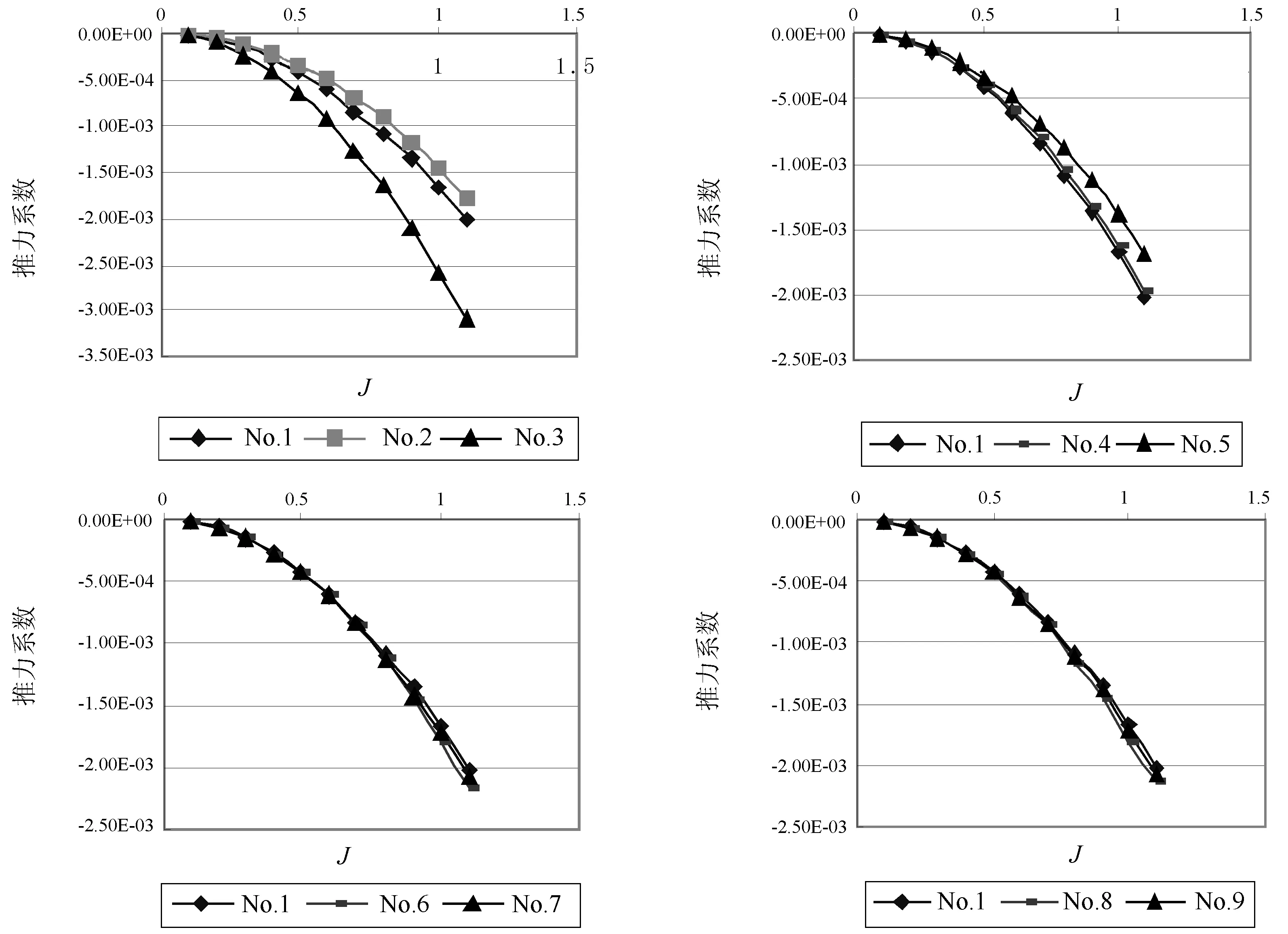
圖9 模型No.1～No.9推力系數曲線圖

4) No.8>No.1>No.9(表明L/D的影響)

由圖9可知， 在J=0.3(設計工況)附近， 各個導管之間的推力系數關系如下：1) No.2>No.1>No.3; 2) No.5>No.4>No.1; 3) No.1>No.7>No.6; 4) No.1>No.9>No.8。

由以上結果可以看出，在文獻推薦的優良導管幾何參數范圍內，α越小，β越大導管所受阻力越小，L/D和Lp/L則是在取中間值時導管的阻力最小。再結合圖8、圖9中數值的變化幅度來看，雖然幾何形狀對推力系數KTD0有影響，L/D、Lp/L影響不是很大，α和β變化影響比較大。不同幾何參數的變化對升阻比CL/CD是有影響的，但β變化影響最大。

5 結 論

1) 要得到較大的推力(較小的阻力)，需要相對較小的收縮系數和較大的擴張系數，而長徑比L/D和平行中體與導管長度比Lp/L則是以標準模型No.1的為好。

2) 流體力學軟件在分析此類問題中能獲得非常真實有用的研究效果。使應用數值方法揭示導管幾何參數對其水動力性能的影響，可降低設計成本，提高工作效率。

[1] 王國強，盛振邦.船舶推進[M].北京：國防工業出版社，1985.

[2] 王福軍.計算流體動力學分析—CFD軟件原理與應用[M].北京：清華大學出版社，2004.

[3] 辛曉華,張武,周華.基于Fluent 的繞流問題的數值模擬與并行計算[J].計算機工程與設計,2005(8)：2153-2154.

[4] 韓占忠，王敬，蘭小平.FLUENT流體工程仿真計算實例與應用[M].北京：北京理工大學出版社.2004.

[5] 何德明，李遠林.船舶前置導管流態的數值計算與分析[J].船舶工程，2004(4)：22-25.

[6] 周天孝,白文.CFD多塊網格生成新進展[J].力學進展，1999,29(3) ：344-368.